Towards prediction of turbulent flows at high Reynolds numbers using high performance computing data and deep learning

In this paper, deep learning (DL) methods are evaluated in the context of turbulent flows. Various generative adversarial networks (GANs) are discussed with respect to their suitability for understanding and modeling turbulence. Wasserstein GANs (WGANs) are then chosen to generate small-scale turbulence. Highly resolved direct numerical simulation (DNS) turbulent data is used for training the WGANs and the effect of network parameters, such as learning rate and loss function, is studied. Qualitatively good agreement between DNS input data and generated turbulent structures is shown. A quantitative statistical assessment of the predicted turbulent fields is performed.

Applying Physics-Informed Enhanced Super-Resolution Generative Adversarial Networks to Turbulent Premixed Combustion and Engine-like Flame Kernel Direct Numerical Simulation Data

Models for finite-rate-chemistry in underresolved flows still pose one of the main challenges for predictive simulations of complex configurations. The problem gets even more challenging if turbulence is involved. This work advances the recently developed PIESRGAN modeling approach to turbulent premixed combustion. For that, the physical information processed by the network and considered in the loss function are adjusted, the training process is smoothed, and especially effects from density changes are considered. The resulting model provides good results for a priori and a posteriori tests on direct numerical simulation data of a fully turbulent premixed flame kernel. The limits of the modeling approach are discussed. Finally, the model is employed to compute further realizations of the premixed flame kernel, which are analyzed with a scale-sensitive framework regarding their cycle-to-cycle variations. The work shows that the data-driven PIESRGAN subfilter model can very accurately reproduce direct numerical simulation data on much coarser meshes, which is hardly possible with classical subfilter models, and enables studying statistical processes more efficiently due to the smaller computing cost.

Using Physics-Informed Super-Resolution Generative Adversarial Networks for Subgrid Modeling in Turbulent Reactive Flows

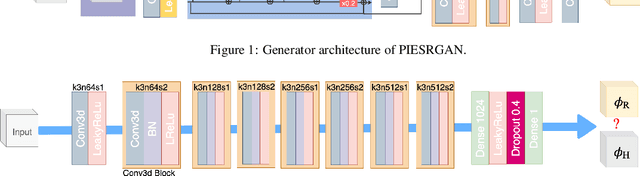
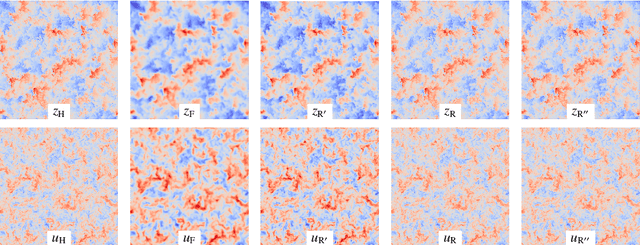
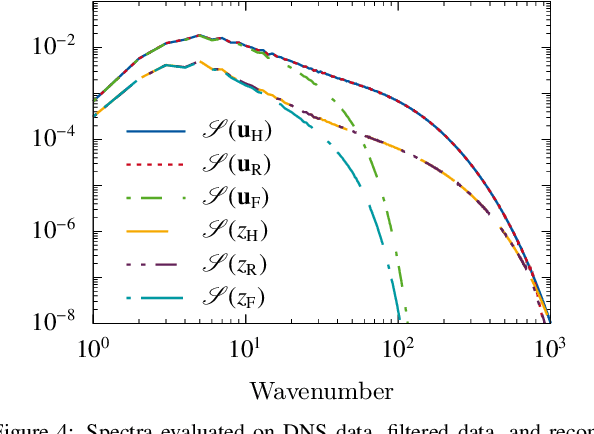
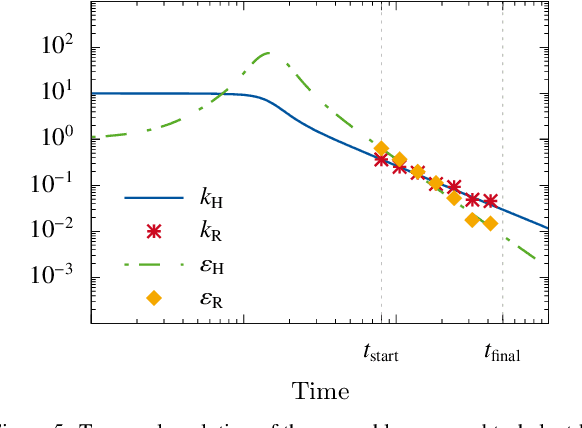
Turbulence is still one of the main challenges for accurately predicting reactive flows. Therefore, the development of new turbulence closures which can be applied to combustion problems is essential. Data-driven modeling has become very popular in many fields over the last years as large, often extensively labeled, datasets became available and training of large neural networks became possible on GPUs speeding up the learning process tremendously. However, the successful application of deep neural networks in fluid dynamics, for example for subgrid modeling in the context of large-eddy simulations (LESs), is still challenging. Reasons for this are the large amount of degrees of freedom in realistic flows, the high requirements with respect to accuracy and error robustness, as well as open questions, such as the generalization capability of trained neural networks in such high-dimensional, physics-constrained scenarios. This work presents a novel subgrid modeling approach based on a generative adversarial network (GAN), which is trained with unsupervised deep learning (DL) using adversarial and physics-informed losses. A two-step training method is used to improve the generalization capability, especially extrapolation, of the network. The novel approach gives good results in a priori as well as a posteriori tests with decaying turbulence including turbulent mixing. The applicability of the network in complex combustion scenarios is furthermore discussed by employing it to a reactive LES of the Spray A case defined by the Engine Combustion Network (ECN).

Deep learning at scale for subgrid modeling in turbulent flows

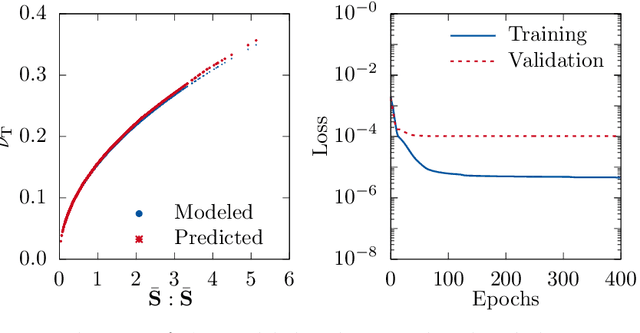
Modeling of turbulent flows is still challenging. One way to deal with the large scale separation due to turbulence is to simulate only the large scales and model the unresolved contributions as done in large-eddy simulation (LES). This paper focuses on two deep learning (DL) strategies, regression and reconstruction, which are data-driven and promising alternatives to classical modeling concepts. Using three-dimensional (3-D) forced turbulence direct numerical simulation (DNS) data, subgrid models are evaluated, which predict the unresolved part of quantities based on the resolved solution. For regression, it is shown that feedforward artificial neural networks (ANNs) are able to predict the fully-resolved scalar dissipation rate using filtered input data. It was found that a combination of a large-scale quantity, such as the filtered passive scalar itself, and a small-scale quantity, such as the filtered energy dissipation rate, gives the best agreement with the actual DNS data. Furthermore, a DL network motivated by enhanced super-resolution generative adversarial networks (ESRGANs) was used to reconstruct fully-resolved 3-D velocity fields from filtered velocity fields. The energy spectrum shows very good agreement. As size of scientific data is often in the order of terabytes or more, DL needs to be combined with high performance computing (HPC). Necessary code improvements for HPC-DL are discussed with respect to the supercomputer JURECA. After optimizing the training code, 396.2 TFLOPS were achieved.

On the self-similarity of line segments in decaying homogeneous isotropic turbulence

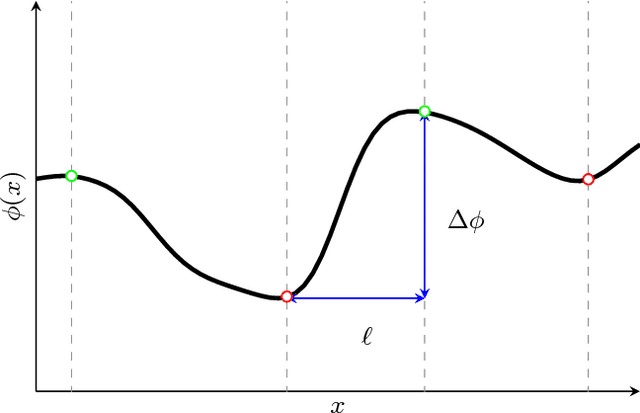
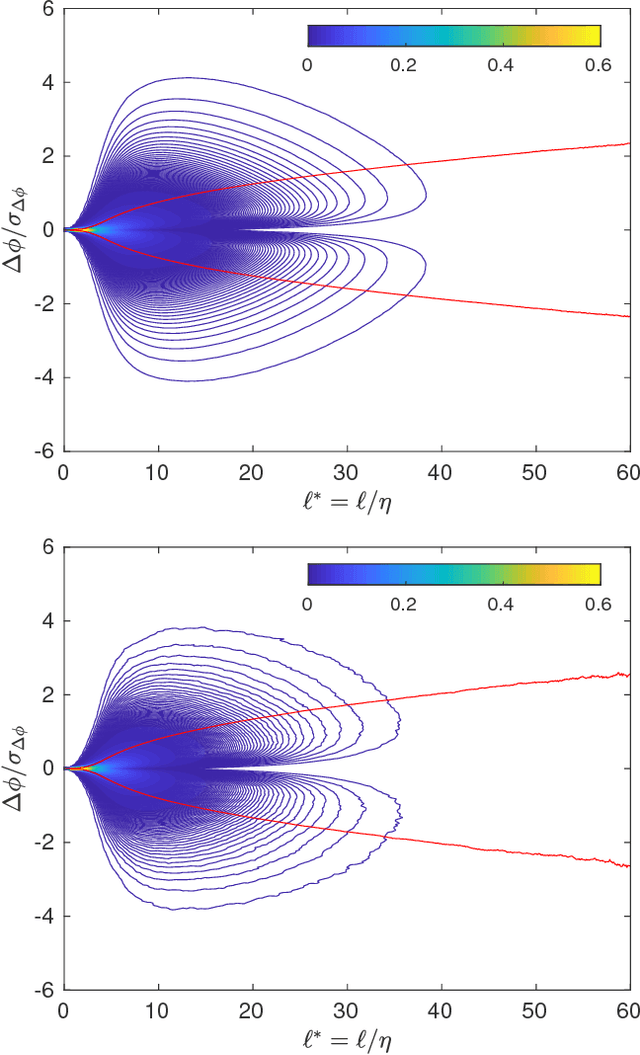
The self-similarity of a passive scalar in homogeneous isotropic decaying turbulence is investigated by the method of line segments (M. Gauding et al., Physics of Fluids 27.9 (2015): 095102). The analysis is based on a highly resolved direct numerical simulation of decaying turbulence. The method of line segments is used to perform a decomposition of the scalar field into smaller sub-units based on the extremal points of the scalar along a straight line. These sub-units (the so-called line segments) are parameterized by their length $\ell$ and the difference $\Delta\phi$ of the scalar field between the ending points. Line segments can be understood as thin local convective-diffusive structures in which diffusive processes are enhanced by compressive strain. From DNS, it is shown that the marginal distribution function of the length~$\ell$ assumes complete self-similarity when re-scaled by the mean length $\ell_m$. The joint statistics of $\Delta\phi$ and $\ell$, from which the local gradient $g=\Delta\phi/\ell$ can be defined, play an important role in understanding the turbulence mixing and flow structure. Large values of $g$ occur at a small but finite length scale. Statistics of $g$ are characterized by rare but strong deviations that exceed the standard deviation by more than one order of magnitude. It is shown that these events break complete self-similarity of line segments, which confirms the standard paradigm of turbulence that intense events (which are known as internal intermittency) are not self-similar.