On the self-similarity of line segments in decaying homogeneous isotropic turbulence
Paper and Code
Sep 20, 2018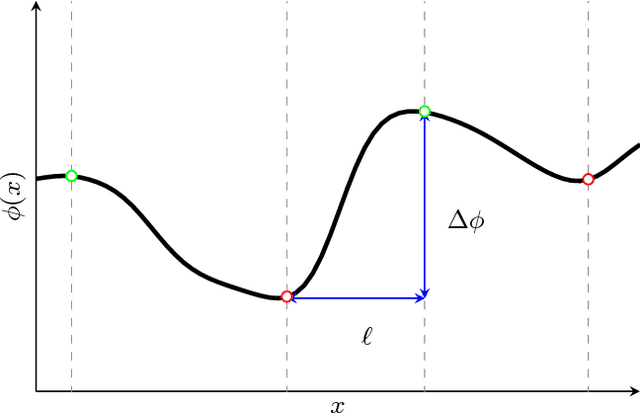

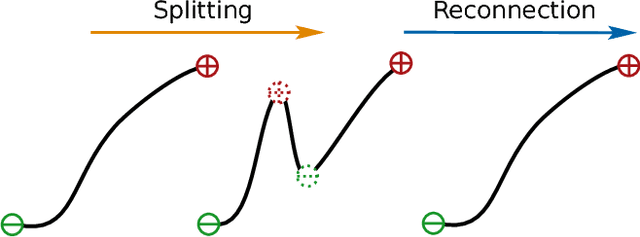
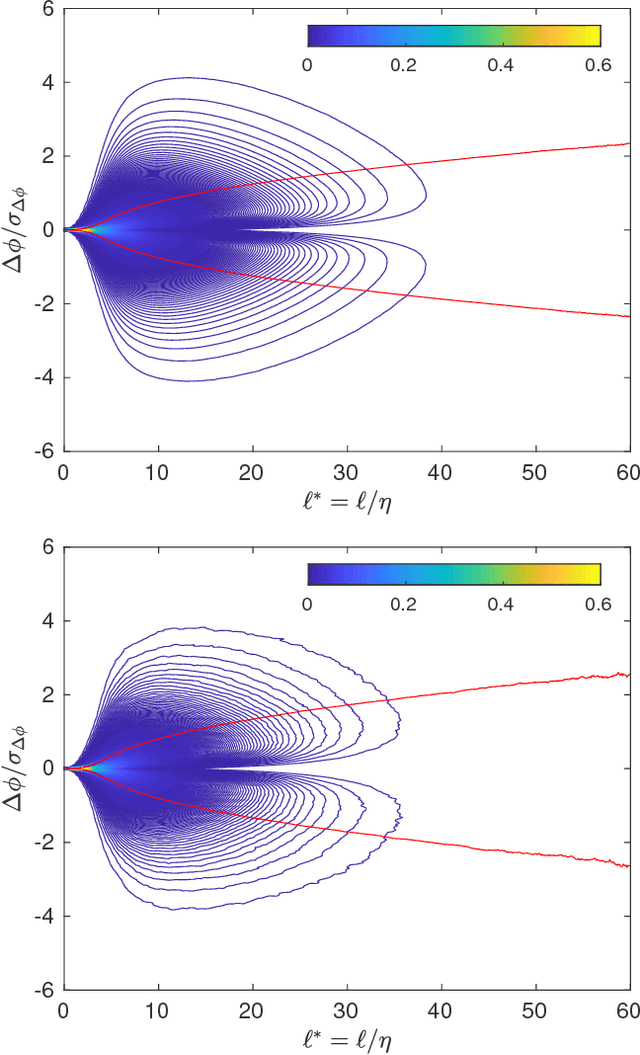
The self-similarity of a passive scalar in homogeneous isotropic decaying turbulence is investigated by the method of line segments (M. Gauding et al., Physics of Fluids 27.9 (2015): 095102). The analysis is based on a highly resolved direct numerical simulation of decaying turbulence. The method of line segments is used to perform a decomposition of the scalar field into smaller sub-units based on the extremal points of the scalar along a straight line. These sub-units (the so-called line segments) are parameterized by their length $\ell$ and the difference $\Delta\phi$ of the scalar field between the ending points. Line segments can be understood as thin local convective-diffusive structures in which diffusive processes are enhanced by compressive strain. From DNS, it is shown that the marginal distribution function of the length~$\ell$ assumes complete self-similarity when re-scaled by the mean length $\ell_m$. The joint statistics of $\Delta\phi$ and $\ell$, from which the local gradient $g=\Delta\phi/\ell$ can be defined, play an important role in understanding the turbulence mixing and flow structure. Large values of $g$ occur at a small but finite length scale. Statistics of $g$ are characterized by rare but strong deviations that exceed the standard deviation by more than one order of magnitude. It is shown that these events break complete self-similarity of line segments, which confirms the standard paradigm of turbulence that intense events (which are known as internal intermittency) are not self-similar.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge