Marissa Masden
Combinatorial Regularity for Relatively Perfect Discrete Morse Gradient Vector Fields of ReLU Neural Networks
Dec 23, 2024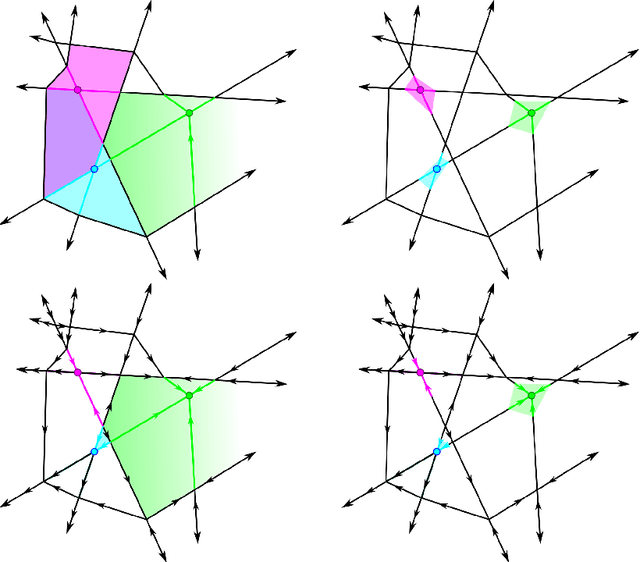

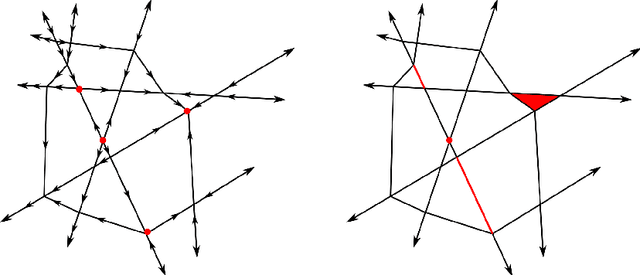
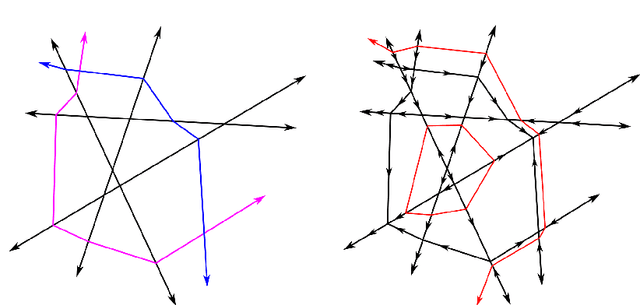
Abstract:One common function class in machine learning is the class of ReLU neural networks. ReLU neural networks induce a piecewise linear decomposition of their input space called the canonical polyhedral complex. It has previously been established that it is decidable whether a ReLU neural network is piecewise linear Morse. In order to expand computational tools for analyzing the topological properties of ReLU neural networks, and to harness the strengths of discrete Morse theory, we introduce a schematic for translating between a given piecewise linear Morse function (e.g. parameters of a ReLU neural network) on a canonical polyhedral complex and a compatible (``relatively perfect") discrete Morse function on the same complex. Our approach is constructive, producing an algorithm that can be used to determine if a given vertex in a canonical polyhedral complex corresponds to a piecewise linear Morse critical point. Furthermore we provide an algorithm for constructing a consistent discrete Morse pairing on cells in the canonical polyhedral complex which contain this vertex. We additionally provide some new realizability results with respect to sublevel set topology in the case of shallow ReLU neural networks.
ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain
Sep 08, 2024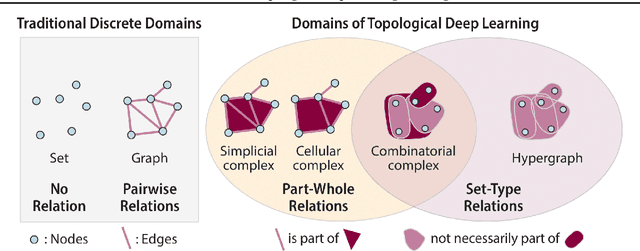
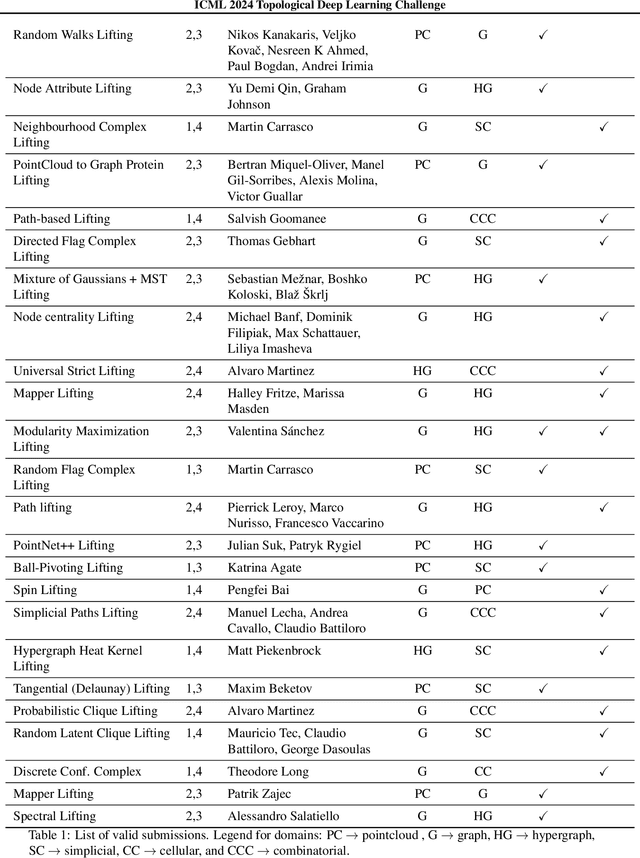
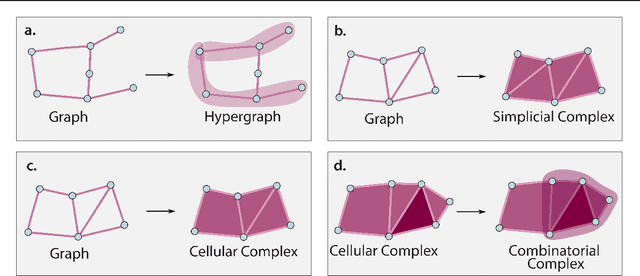
Abstract:This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.
Automated Grain Boundary (GB) Segmentation and Microstructural Analysis in 347H Stainless Steel Using Deep Learning and Multimodal Microscopy
May 12, 2023


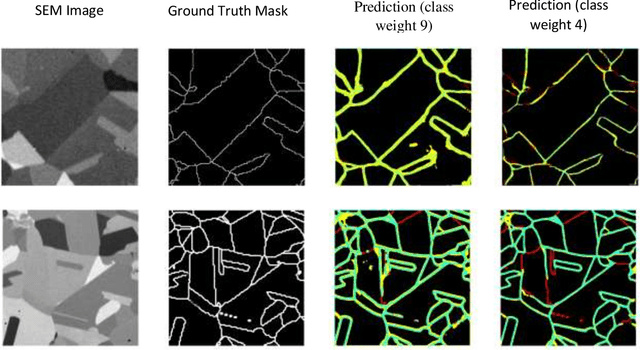
Abstract:Austenitic 347H stainless steel offers superior mechanical properties and corrosion resistance required for extreme operating conditions such as high temperature. The change in microstructure due to composition and process variations is expected to impact material properties. Identifying microstructural features such as grain boundaries thus becomes an important task in the process-microstructure-properties loop. Applying convolutional neural network (CNN) based deep-learning models is a powerful technique to detect features from material micrographs in an automated manner. Manual labeling of the images for the segmentation task poses a major bottleneck for generating training data and labels in a reliable and reproducible way within a reasonable timeframe. In this study, we attempt to overcome such limitations by utilizing multi-modal microscopy to generate labels directly instead of manual labeling. We combine scanning electron microscopy (SEM) images of 347H stainless steel as training data and electron backscatter diffraction (EBSD) micrographs as pixel-wise labels for grain boundary detection as a semantic segmentation task. We demonstrate that despite producing instrumentation drift during data collection between two modes of microscopy, this method performs comparably to similar segmentation tasks that used manual labeling. Additionally, we find that na\"ive pixel-wise segmentation results in small gaps and missing boundaries in the predicted grain boundary map. By incorporating topological information during model training, the connectivity of the grain boundary network and segmentation performance is improved. Finally, our approach is validated by accurate computation on downstream tasks of predicting the underlying grain morphology distributions which are the ultimate quantities of interest for microstructural characterization.
Algorithmic Determination of the Combinatorial Structure of the Linear Regions of ReLU Neural Networks
Jul 15, 2022


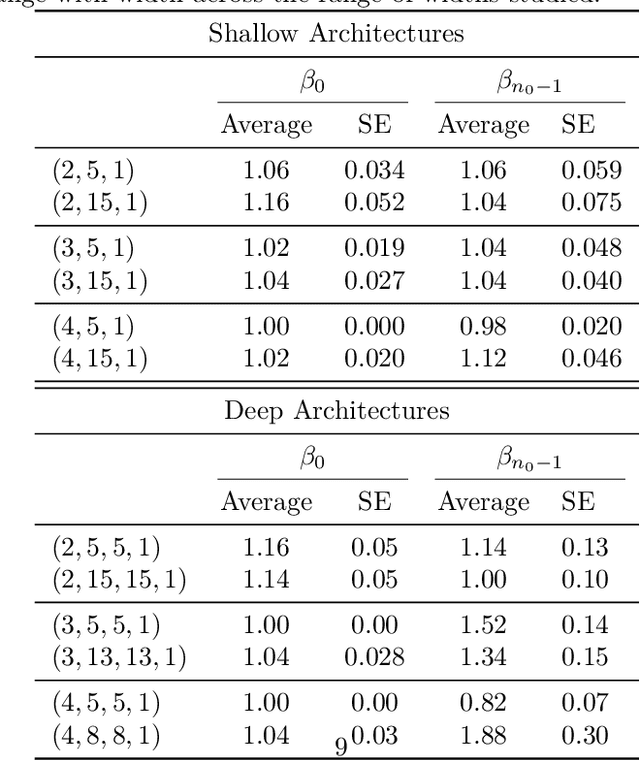
Abstract:We algorithmically determine the regions and facets of all dimensions of the canonical polyhedral complex, the universal object into which a ReLU network decomposes its input space. We show that the locations of the vertices of the canonical polyhedral complex along with their signs with respect to layer maps determine the full facet structure across all dimensions. We present an algorithm which calculates this full combinatorial structure, making use of our theorems that the dual complex to the canonical polyhedral complex is cubical and it possesses a multiplication compatible with its facet structure. The resulting algorithm is numerically stable, polynomial time in the number of intermediate neurons, and obtains accurate information across all dimensions. This permits us to obtain, for example, the true topology of the decision boundaries of networks with low-dimensional inputs. We run empirics on such networks at initialization, finding that width alone does not increase observed topology, but width in the presence of depth does. Source code for our algorithms is accessible online at https://github.com/mmasden/canonicalpoly.
Local and global topological complexity measures OF ReLU neural network functions
Apr 12, 2022
Abstract:We apply a generalized piecewise-linear (PL) version of Morse theory due to Grunert-Kuhnel-Rote to define and study new local and global notions of topological complexity for fully-connected feedforward ReLU neural network functions, F: R^n -> R. Along the way, we show how to construct, for each such F, a canonical polytopal complex K(F) and a deformation retract of the domain onto K(F), yielding a convenient compact model for performing calculations. We also give a combinatorial description of local complexity for depth 2 networks, and a construction showing that local complexity can be arbitrarily high.
Linear discriminant initialization for feed-forward neural networks
Aug 18, 2020
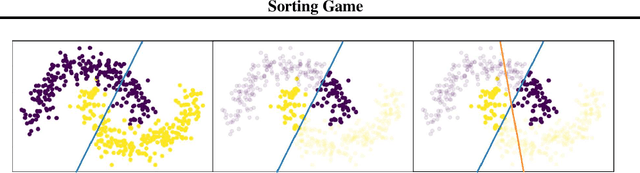
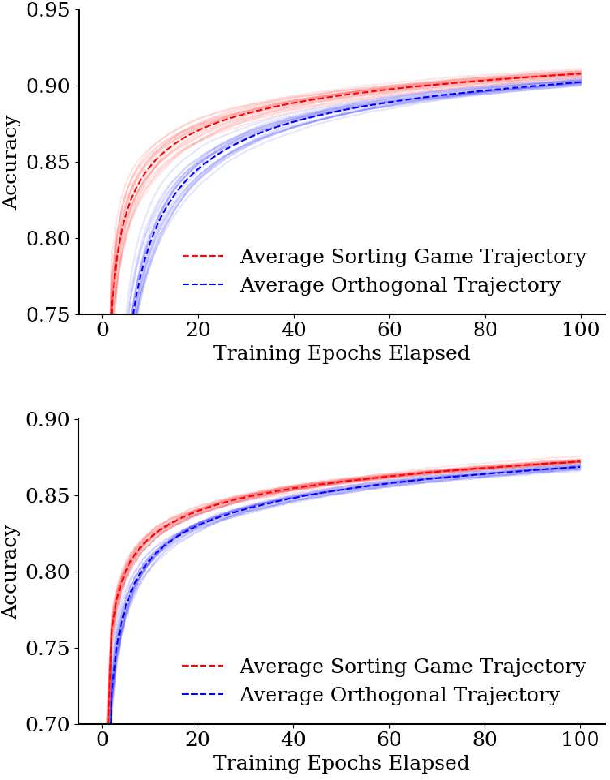

Abstract:Informed by the basic geometry underlying feed forward neural networks, we initialize the weights of the first layer of a neural network using the linear discriminants which best distinguish individual classes. Networks initialized in this way take fewer training steps to reach the same level of training, and asymptotically have higher accuracy on training data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge