Generating gradients in the energy landscape using rectified linear type cost functions for efficiently solving 0/1 matrix factorization in Simulated Annealing

The 0/1 matrix factorization defines matrix products using logical AND and OR as product-sum operators, revealing the factors influencing various decision processes. Instances and their characteristics are arranged in rows and columns. Formulating matrix factorization as an energy minimization problem and exploring it with Simulated Annealing (SA) theoretically enables finding a minimum solution in sufficient time. However, searching for the optimal solution in practical time becomes problematic when the energy landscape has many plateaus with flat slopes. In this work, we propose a method to facilitate the solution process by applying a gradient to the energy landscape, using a rectified linear type cost function readily available in modern annealing machines. We also propose a method to quickly obtain a solution by updating the cost function's gradient during the search process. Numerical experiments were conducted, confirming the method's effectiveness with both noise-free artificial and real data.

Characterization of Locality in Spin States and Forced Moves for Optimizations

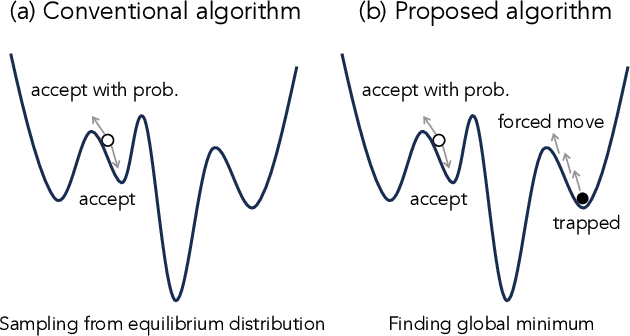
Ising formulations are widely utilized to solve combinatorial optimization problems, and a variety of quantum or semiconductor-based hardware has recently been made available. In combinatorial optimization problems, the existence of local minima in energy landscapes is problematic to use to seek the global minimum. We note that the aim of the optimization is not to obtain exact samplings from the Boltzmann distribution, and there is thus no need to satisfy detailed balance conditions. In light of this fact, we develop an algorithm to get out of the local minima efficiently while it does not yield the exact samplings. For this purpose, we utilize a feature that characterizes locality in the current state, which is easy to obtain with a type of specialized hardware. Furthermore, as the proposed algorithm is based on a rejection-free algorithm, the computational cost is low. In this work, after presenting the details of the proposed algorithm, we report the results of numerical experiments that demonstrate the effectiveness of the proposed feature and algorithm.

Efficient correlation-based discretization of continuous variables for annealing machines

Annealing machines specialized for combinatorial optimization problems have been developed, and some companies offer services to use those machines. Such specialized machines can only handle binary variables, and their input format is the quadratic unconstrained binary optimization (QUBO) formulation. Therefore, discretization is necessary to solve problems with continuous variables. However, there is a severe constraint on the number of binary variables with such machines. Although the simple binary expansion in the previous research requires many binary variables, we need to reduce the number of such variables in the QUBO formulation due to the constraint. We propose a discretization method that involves using correlations of continuous variables. We numerically show that the proposed method reduces the number of necessary binary variables in the QUBO formulation without a significant loss in prediction accuracy.

Derivation of QUBO formulations for sparse estimation

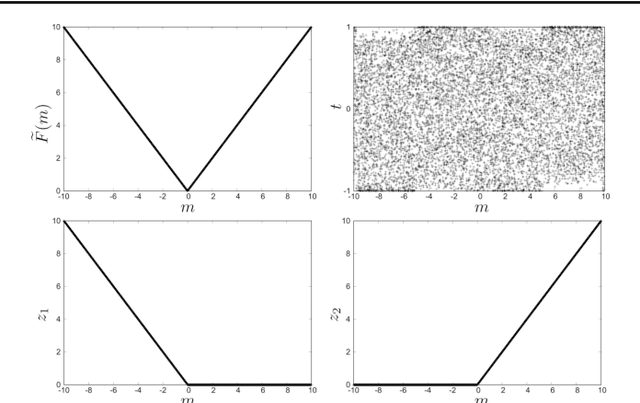
We propose a quadratic unconstrained binary optimization (QUBO) formulation of the l1-norm, which enables us to perform sparse estimation of Ising-type annealing methods such as quantum annealing. The QUBO formulation is derived using the Legendre transformation and the Wolfe theorem, which have recently been employed to derive the QUBO formulations of ReLU-type functions. It is shown that a simple application of the derivation method to the l1-norm case results in a redundant variable. Finally a simplified QUBO formulation is obtained by removing the redundant variable.

Markov Chain Monte Carlo for Arrangement of Hyperplanes in Locality-Sensitive Hashing

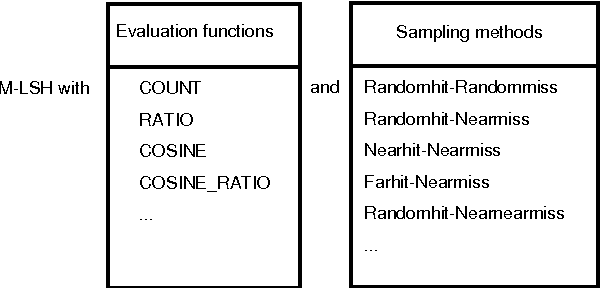
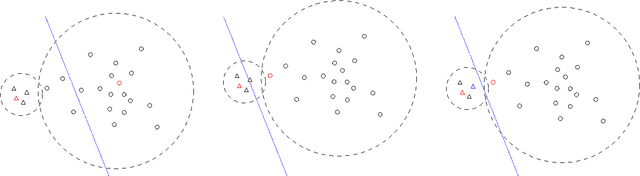
Since Hamming distances can be calculated by bitwise computations, they can be calculated with less computational load than L2 distances. Similarity searches can therefore be performed faster in Hamming distance space. The elements of Hamming distance space are bit strings. On the other hand, the arrangement of hyperplanes induce the transformation from the feature vectors into feature bit strings. This transformation method is a type of locality-sensitive hashing that has been attracting attention as a way of performing approximate similarity searches at high speed. Supervised learning of hyperplane arrangements allows us to obtain a method that transforms them into feature bit strings reflecting the information of labels applied to higher-dimensional feature vectors. In this p aper, we propose a supervised learning method for hyperplane arrangements in feature space that uses a Markov chain Monte Carlo (MCMC) method. We consider the probability density functions used during learning, and evaluate their performance. We also consider the sampling method for learning data pairs needed in learning, and we evaluate its performance. We confirm that the accuracy of this learning method when using a suitable probability density function and sampling method is greater than the accuracy of existing learning methods.

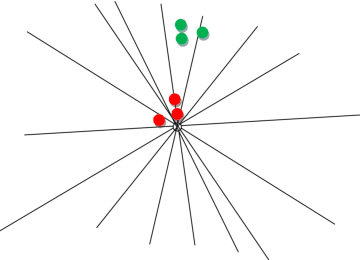
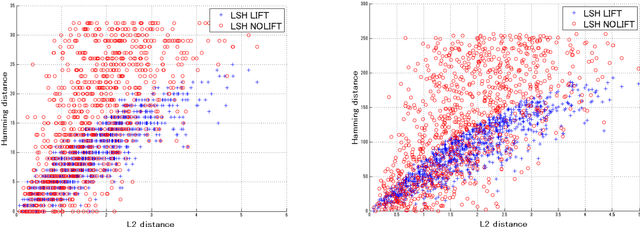
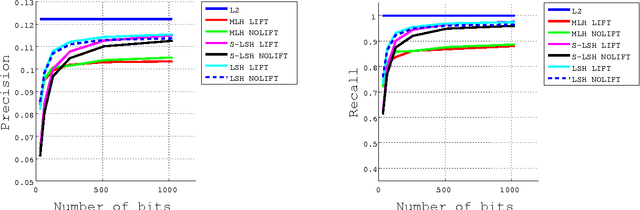
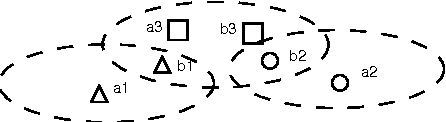
Hyperplane Arrangements and Locality-Sensitive Hashing with Lift

Locality-sensitive hashing converts high-dimensional feature vectors, such as image and speech, into bit arrays and allows high-speed similarity calculation with the Hamming distance. There is a hashing scheme that maps feature vectors to bit arrays depending on the signs of the inner products between feature vectors and the normal vectors of hyperplanes placed in the feature space. This hashing can be seen as a discretization of the feature space by hyperplanes. If labels for data are given, one can determine the hyperplanes by using learning algorithms. However, many proposed learning methods do not consider the hyperplanes' offsets. Not doing so decreases the number of partitioned regions, and the correlation between Hamming distances and Euclidean distances becomes small. In this paper, we propose a lift map that converts learning algorithms without the offsets to the ones that take into account the offsets. With this method, the learning methods without the offsets give the discretizations of spaces as if it takes into account the offsets. For the proposed method, we input several high-dimensional feature data sets and studied the relationship between the statistical characteristics of data, the number of hyperplanes, and the effect of the proposed method.

Locality-Sensitive Hashing with Margin Based Feature Selection

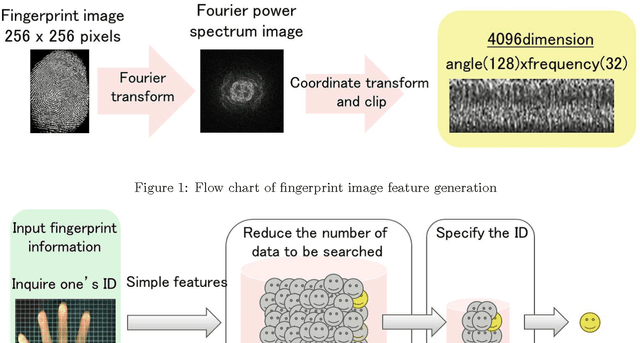
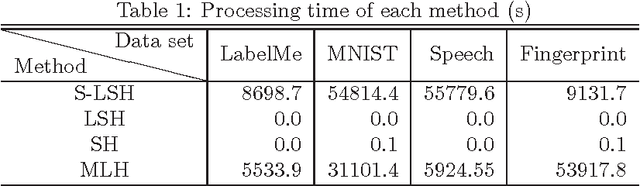
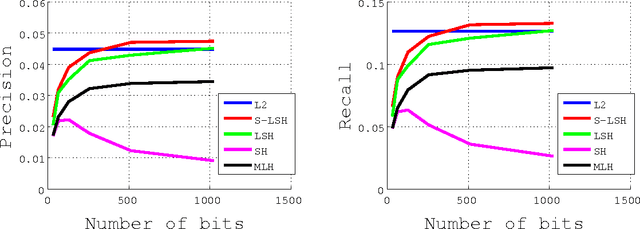
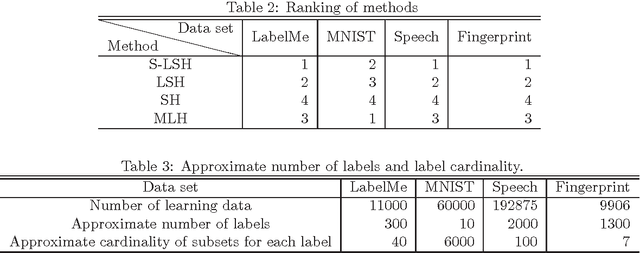
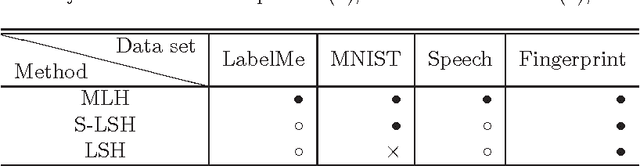
We propose a learning method with feature selection for Locality-Sensitive Hashing. Locality-Sensitive Hashing converts feature vectors into bit arrays. These bit arrays can be used to perform similarity searches and personal authentication. The proposed method uses bit arrays longer than those used in the end for similarity and other searches and by learning selects the bits that will be used. We demonstrated this method can effectively perform optimization for cases such as fingerprint images with a large number of labels and extremely few data that share the same labels, as well as verifying that it is also effective for natural images, handwritten digits, and speech features.