Derivation of QUBO formulations for sparse estimation
Paper and Code
Jan 27, 2020
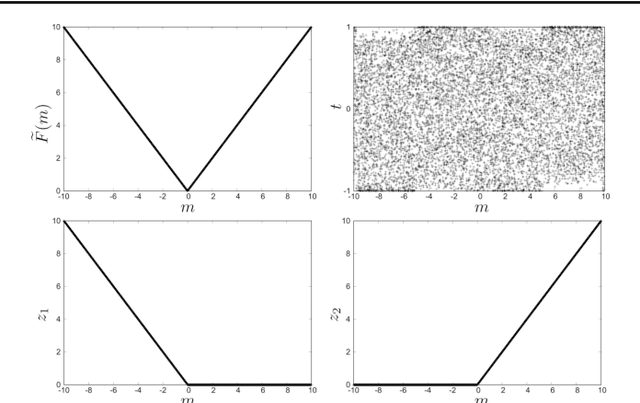
We propose a quadratic unconstrained binary optimization (QUBO) formulation of the l1-norm, which enables us to perform sparse estimation of Ising-type annealing methods such as quantum annealing. The QUBO formulation is derived using the Legendre transformation and the Wolfe theorem, which have recently been employed to derive the QUBO formulations of ReLU-type functions. It is shown that a simple application of the derivation method to the l1-norm case results in a redundant variable. Finally a simplified QUBO formulation is obtained by removing the redundant variable.
* 5 pages, 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge