Generating gradients in the energy landscape using rectified linear type cost functions for efficiently solving 0/1 matrix factorization in Simulated Annealing

The 0/1 matrix factorization defines matrix products using logical AND and OR as product-sum operators, revealing the factors influencing various decision processes. Instances and their characteristics are arranged in rows and columns. Formulating matrix factorization as an energy minimization problem and exploring it with Simulated Annealing (SA) theoretically enables finding a minimum solution in sufficient time. However, searching for the optimal solution in practical time becomes problematic when the energy landscape has many plateaus with flat slopes. In this work, we propose a method to facilitate the solution process by applying a gradient to the energy landscape, using a rectified linear type cost function readily available in modern annealing machines. We also propose a method to quickly obtain a solution by updating the cost function's gradient during the search process. Numerical experiments were conducted, confirming the method's effectiveness with both noise-free artificial and real data.

Characterization of Locality in Spin States and Forced Moves for Optimizations

Ising formulations are widely utilized to solve combinatorial optimization problems, and a variety of quantum or semiconductor-based hardware has recently been made available. In combinatorial optimization problems, the existence of local minima in energy landscapes is problematic to use to seek the global minimum. We note that the aim of the optimization is not to obtain exact samplings from the Boltzmann distribution, and there is thus no need to satisfy detailed balance conditions. In light of this fact, we develop an algorithm to get out of the local minima efficiently while it does not yield the exact samplings. For this purpose, we utilize a feature that characterizes locality in the current state, which is easy to obtain with a type of specialized hardware. Furthermore, as the proposed algorithm is based on a rejection-free algorithm, the computational cost is low. In this work, after presenting the details of the proposed algorithm, we report the results of numerical experiments that demonstrate the effectiveness of the proposed feature and algorithm.

Efficient correlation-based discretization of continuous variables for annealing machines

Annealing machines specialized for combinatorial optimization problems have been developed, and some companies offer services to use those machines. Such specialized machines can only handle binary variables, and their input format is the quadratic unconstrained binary optimization (QUBO) formulation. Therefore, discretization is necessary to solve problems with continuous variables. However, there is a severe constraint on the number of binary variables with such machines. Although the simple binary expansion in the previous research requires many binary variables, we need to reduce the number of such variables in the QUBO formulation due to the constraint. We propose a discretization method that involves using correlations of continuous variables. We numerically show that the proposed method reduces the number of necessary binary variables in the QUBO formulation without a significant loss in prediction accuracy.

Derivation of QUBO formulations for sparse estimation

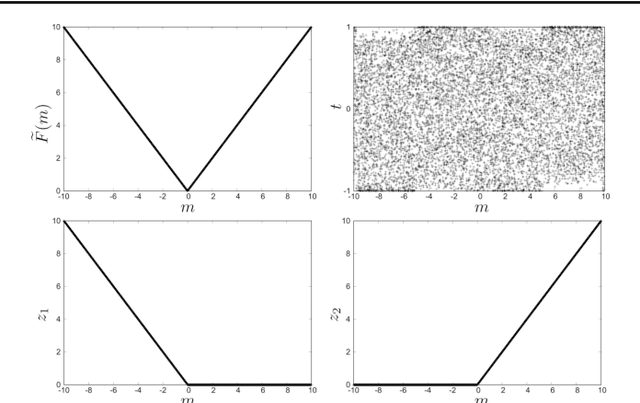
We propose a quadratic unconstrained binary optimization (QUBO) formulation of the l1-norm, which enables us to perform sparse estimation of Ising-type annealing methods such as quantum annealing. The QUBO formulation is derived using the Legendre transformation and the Wolfe theorem, which have recently been employed to derive the QUBO formulations of ReLU-type functions. It is shown that a simple application of the derivation method to the l1-norm case results in a redundant variable. Finally a simplified QUBO formulation is obtained by removing the redundant variable.