Characterization of Locality in Spin States and Forced Moves for Optimizations
Paper and Code
Dec 05, 2023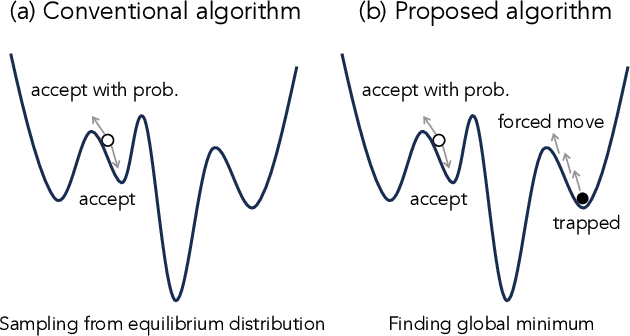


Ising formulations are widely utilized to solve combinatorial optimization problems, and a variety of quantum or semiconductor-based hardware has recently been made available. In combinatorial optimization problems, the existence of local minima in energy landscapes is problematic to use to seek the global minimum. We note that the aim of the optimization is not to obtain exact samplings from the Boltzmann distribution, and there is thus no need to satisfy detailed balance conditions. In light of this fact, we develop an algorithm to get out of the local minima efficiently while it does not yield the exact samplings. For this purpose, we utilize a feature that characterizes locality in the current state, which is easy to obtain with a type of specialized hardware. Furthermore, as the proposed algorithm is based on a rejection-free algorithm, the computational cost is low. In this work, after presenting the details of the proposed algorithm, we report the results of numerical experiments that demonstrate the effectiveness of the proposed feature and algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge