Aspects of importance sampling in parameter selection for neural networks using ridgelet transform

The choice of parameters in neural networks is crucial in the performance, and an oracle distribution derived from the ridgelet transform enables us to obtain suitable initial parameters. In other words, the distribution of parameters is connected to the integral representation of target functions. The oracle distribution allows us to avoid the conventional backpropagation learning process; only a linear regression is enough to construct the neural network in simple cases. This study provides a new look at the oracle distributions and ridgelet transforms, i.e., an aspect of importance sampling. In addition, we propose extensions of the parameter sampling methods. We demonstrate the aspect of importance sampling and the proposed sampling algorithms via one-dimensional and high-dimensional examples; the results imply that the magnitude of weight parameters could be more crucial than the intercept parameters.

Compression of the Koopman matrix for nonlinear physical models via hierarchical clustering

Machine learning methods allow the prediction of nonlinear dynamical systems from data alone. The Koopman operator is one of them, which enables us to employ linear analysis for nonlinear dynamical systems. The linear characteristics of the Koopman operator are hopeful to understand the nonlinear dynamics and perform rapid predictions. The extended dynamic mode decomposition (EDMD) is one of the methods to approximate the Koopman operator as a finite-dimensional matrix. In this work, we propose a method to compress the Koopman matrix using hierarchical clustering. Numerical demonstrations for the cart-pole model and comparisons with the conventional singular value decomposition (SVD) are shown; the results indicate that the hierarchical clustering performs better than the naive SVD compressions.

Extraction of nonlinearity in neural networks and model compression with Koopman operator

Nonlinearity plays a crucial role in deep neural networks. In this paper, we first investigate the degree to which the nonlinearity of the neural network is essential. For this purpose, we employ the Koopman operator, extended dynamic mode decomposition, and the tensor-train format. The results imply that restricted nonlinearity is enough for the classification of handwritten numbers. Then, we propose a model compression method for deep neural networks, which could be beneficial to handling large networks in resource-constrained environments. Leveraging the Koopman operator, the proposed method enables us to use linear algebra in the internal processing of neural networks. We numerically show that the proposed method performs comparably or better than conventional methods in highly compressed model settings for the handwritten number recognition task.

Attention-Enhanced Reservoir Computing

Photonic reservoir computing has been recently utilized in time series forecasting as the need for hardware implementations to accelerate these predictions has increased. Forecasting chaotic time series remains a significant challenge, an area where the conventional reservoir computing framework encounters limitations of prediction accuracy. We introduce an attention mechanism to the reservoir computing model in the output stage. This attention layer is designed to prioritize distinct features and temporal sequences, thereby substantially enhancing the forecasting accuracy. Our results show that a photonic reservoir computer enhanced with the attention mechanism exhibits improved forecasting capabilities for smaller reservoirs. These advancements highlight the transformative possibilities of reservoir computing for practical applications where accurate forecasting of chaotic time series is crucial.

Characterization of Locality in Spin States and Forced Moves for Optimizations

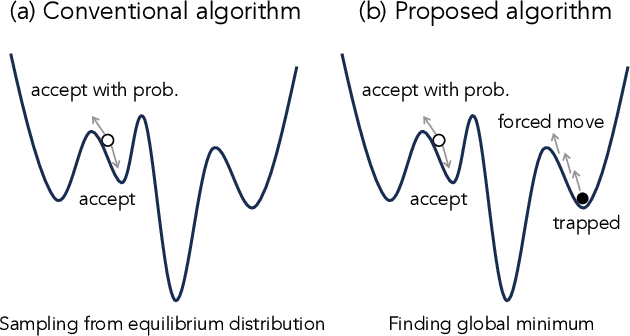
Ising formulations are widely utilized to solve combinatorial optimization problems, and a variety of quantum or semiconductor-based hardware has recently been made available. In combinatorial optimization problems, the existence of local minima in energy landscapes is problematic to use to seek the global minimum. We note that the aim of the optimization is not to obtain exact samplings from the Boltzmann distribution, and there is thus no need to satisfy detailed balance conditions. In light of this fact, we develop an algorithm to get out of the local minima efficiently while it does not yield the exact samplings. For this purpose, we utilize a feature that characterizes locality in the current state, which is easy to obtain with a type of specialized hardware. Furthermore, as the proposed algorithm is based on a rejection-free algorithm, the computational cost is low. In this work, after presenting the details of the proposed algorithm, we report the results of numerical experiments that demonstrate the effectiveness of the proposed feature and algorithm.

Embedding stochastic differential equations into neural networks via dual processes

We propose a new approach to constructing a neural network for predicting expectations of stochastic differential equations. The proposed method does not need data sets of inputs and outputs; instead, the information obtained from the time-evolution equations, i.e., the corresponding dual process, is directly compared with the weights in the neural network. As a demonstration, we construct neural networks for the Ornstein-Uhlenbeck process and the noisy van der Pol system. The remarkable feature of learned networks with the proposed method is the accuracy of inputs near the origin. Hence, it would be possible to avoid the overfitting problem because the learned network does not depend on training data sets.

Efficient correlation-based discretization of continuous variables for annealing machines

Annealing machines specialized for combinatorial optimization problems have been developed, and some companies offer services to use those machines. Such specialized machines can only handle binary variables, and their input format is the quadratic unconstrained binary optimization (QUBO) formulation. Therefore, discretization is necessary to solve problems with continuous variables. However, there is a severe constraint on the number of binary variables with such machines. Although the simple binary expansion in the previous research requires many binary variables, we need to reduce the number of such variables in the QUBO formulation due to the constraint. We propose a discretization method that involves using correlations of continuous variables. We numerically show that the proposed method reduces the number of necessary binary variables in the QUBO formulation without a significant loss in prediction accuracy.

STDP enhances learning by backpropagation in a spiking neural network

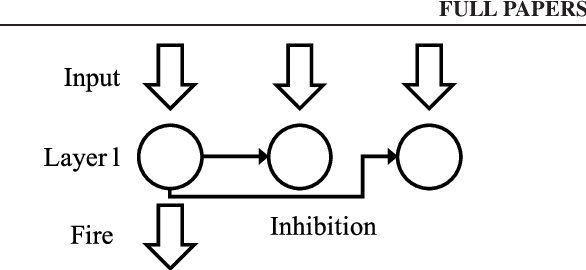
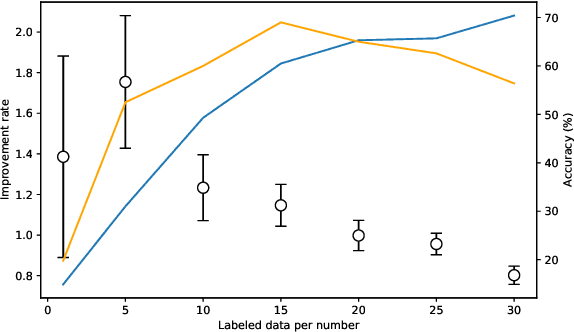
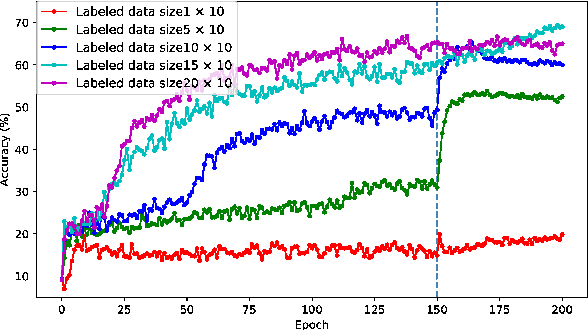
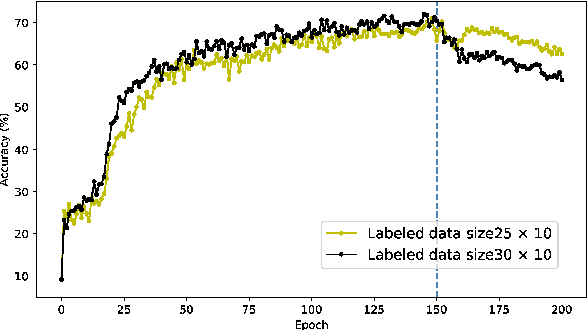
A semi-supervised learning method for spiking neural networks is proposed. The proposed method consists of supervised learning by backpropagation and subsequent unsupervised learning by spike-timing-dependent plasticity (STDP), which is a biologically plausible learning rule. Numerical experiments show that the proposed method improves the accuracy without additional labeling when a small amount of labeled data is used. This feature has not been achieved by existing semi-supervised learning methods of discriminative models. It is possible to implement the proposed learning method for event-driven systems. Hence, it would be highly efficient in real-time problems if it were implemented on neuromorphic hardware. The results suggest that STDP plays an important role other than self-organization when applied after supervised learning, which differs from the previous method of using STDP as pre-training interpreted as self-organization.

Derivation of QUBO formulations for sparse estimation

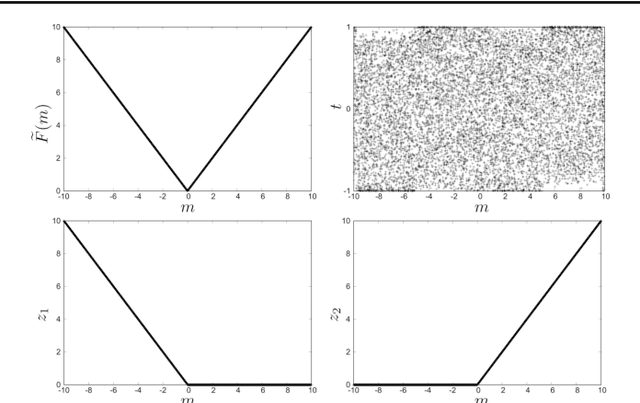
We propose a quadratic unconstrained binary optimization (QUBO) formulation of the l1-norm, which enables us to perform sparse estimation of Ising-type annealing methods such as quantum annealing. The QUBO formulation is derived using the Legendre transformation and the Wolfe theorem, which have recently been employed to derive the QUBO formulations of ReLU-type functions. It is shown that a simple application of the derivation method to the l1-norm case results in a redundant variable. Finally a simplified QUBO formulation is obtained by removing the redundant variable.