Hyperplane Arrangements and Locality-Sensitive Hashing with Lift
Paper and Code
Dec 26, 2012
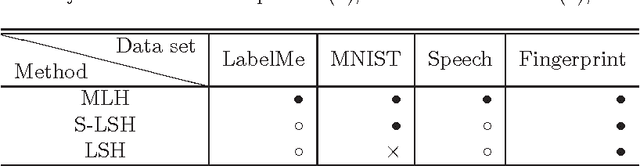
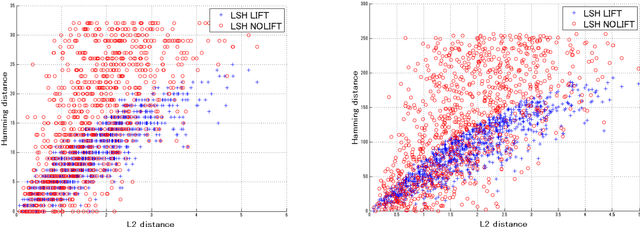
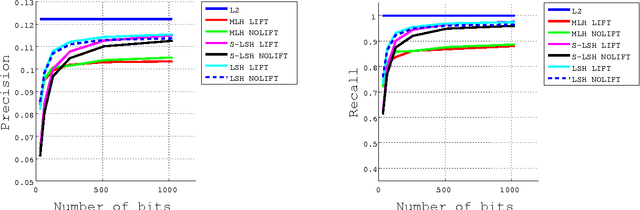
Locality-sensitive hashing converts high-dimensional feature vectors, such as image and speech, into bit arrays and allows high-speed similarity calculation with the Hamming distance. There is a hashing scheme that maps feature vectors to bit arrays depending on the signs of the inner products between feature vectors and the normal vectors of hyperplanes placed in the feature space. This hashing can be seen as a discretization of the feature space by hyperplanes. If labels for data are given, one can determine the hyperplanes by using learning algorithms. However, many proposed learning methods do not consider the hyperplanes' offsets. Not doing so decreases the number of partitioned regions, and the correlation between Hamming distances and Euclidean distances becomes small. In this paper, we propose a lift map that converts learning algorithms without the offsets to the ones that take into account the offsets. With this method, the learning methods without the offsets give the discretizations of spaces as if it takes into account the offsets. For the proposed method, we input several high-dimensional feature data sets and studied the relationship between the statistical characteristics of data, the number of hyperplanes, and the effect of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge