Markov Chain Monte Carlo for Arrangement of Hyperplanes in Locality-Sensitive Hashing
Paper and Code
Mar 18, 2013
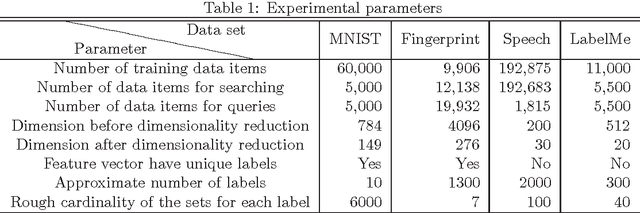
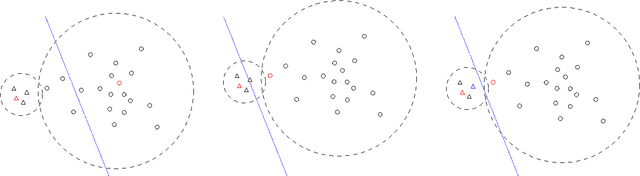
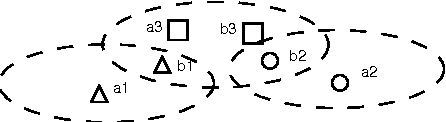
Since Hamming distances can be calculated by bitwise computations, they can be calculated with less computational load than L2 distances. Similarity searches can therefore be performed faster in Hamming distance space. The elements of Hamming distance space are bit strings. On the other hand, the arrangement of hyperplanes induce the transformation from the feature vectors into feature bit strings. This transformation method is a type of locality-sensitive hashing that has been attracting attention as a way of performing approximate similarity searches at high speed. Supervised learning of hyperplane arrangements allows us to obtain a method that transforms them into feature bit strings reflecting the information of labels applied to higher-dimensional feature vectors. In this p aper, we propose a supervised learning method for hyperplane arrangements in feature space that uses a Markov chain Monte Carlo (MCMC) method. We consider the probability density functions used during learning, and evaluate their performance. We also consider the sampling method for learning data pairs needed in learning, and we evaluate its performance. We confirm that the accuracy of this learning method when using a suitable probability density function and sampling method is greater than the accuracy of existing learning methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge