CAGE: Causality-Aware Shapley Value for Global Explanations

As Artificial Intelligence (AI) is having more influence on our everyday lives, it becomes important that AI-based decisions are transparent and explainable. As a consequence, the field of eXplainable AI (or XAI) has become popular in recent years. One way to explain AI models is to elucidate the predictive importance of the input features for the AI model in general, also referred to as global explanations. Inspired by cooperative game theory, Shapley values offer a convenient way for quantifying the feature importance as explanations. However many methods based on Shapley values are built on the assumption of feature independence and often overlook causal relations of the features which could impact their importance for the ML model. Inspired by studies of explanations at the local level, we propose CAGE (Causally-Aware Shapley Values for Global Explanations). In particular, we introduce a novel sampling procedure for out-coalition features that respects the causal relations of the input features. We derive a practical approach that incorporates causal knowledge into global explanation and offers the possibility to interpret the predictive feature importance considering their causal relation. We evaluate our method on synthetic data and real-world data. The explanations from our approach suggest that they are not only more intuitive but also more faithful compared to previous global explanation methods.

Unveiling and unraveling aggregation and dispersion fallacies in group MCDM

Priorities in multi-criteria decision-making (MCDM) convey the relevance preference of one criterion over another, which is usually reflected by imposing the non-negativity and unit-sum constraints. The processing of such priorities is different than other unconstrained data, but this point is often neglected by researchers, which results in fallacious statistical analysis. This article studies three prevalent fallacies in group MCDM along with solutions based on compositional data analysis to avoid misusing statistical operations. First, we use a compositional approach to aggregate the priorities of a group of DMs and show that the outcome of the compositional analysis is identical to the normalized geometric mean, meaning that the arithmetic mean should be avoided. Furthermore, a new aggregation method is developed, which is a robust surrogate for the geometric mean. We also discuss the errors in computing measures of dispersion, including standard deviation and distance functions. Discussing the fallacies in computing the standard deviation, we provide a probabilistic criteria ranking by developing proper Bayesian tests, where we calculate the extent to which a criterion is more important than another. Finally, we explain the errors in computing the distance between priorities, and a clustering algorithm is specially tailored based on proper distance metrics.

Unified Bayesian Frameworks for Multi-criteria Decision-making

This paper presents a Bayesian framework predicated on a probabilistic interpretation of the MCDM problems and encompasses several well-known multi-criteria decision-making (MCDM) methods. Owing to the flexibility of Bayesian models, the proposed framework can address several long-standing, fundamental challenges in MCDM, including group decision-making problems and criteria correlation, in a statistically elegant way. Also, the model can accommodate different forms of uncertainty in the preferences of the decision makers (DMs), such as normal and triangular distributions and interval preferences. Further, a probabilistic mixture model is developed that can group the DMs into several exhaustive classes. A probabilistic ranking scheme is also designed for both criteria and alternatives, where it identifies the extent to which one criterion/alternative is more important than another based on the DM(s) preferences. The experiments validate the outcome of the proposed framework on several numerical examples and highlight its salient features compared to other methods.

Local Explanations for Clinical Search Engine results

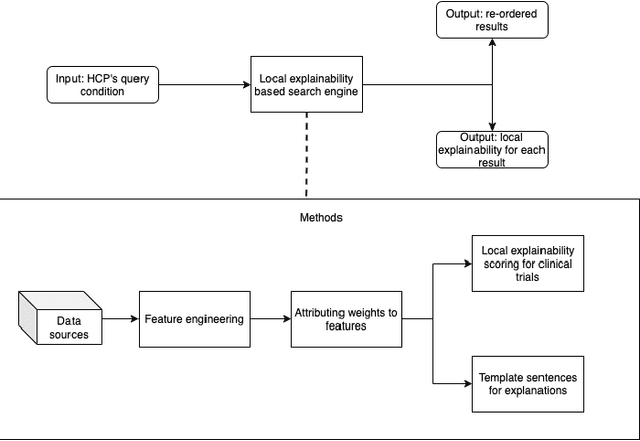
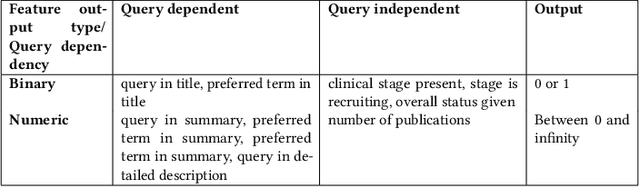
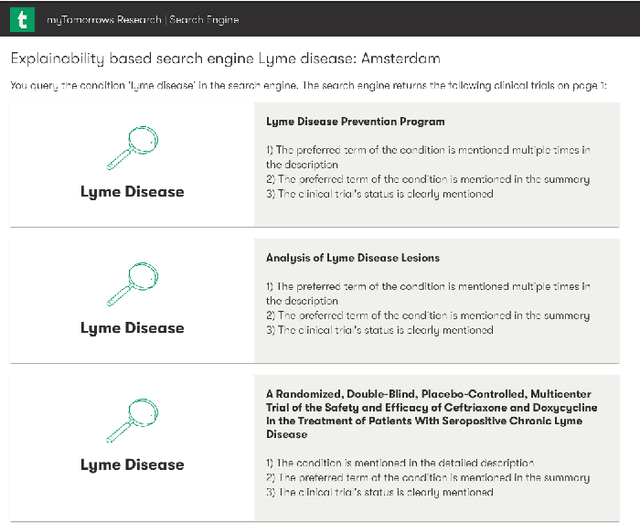
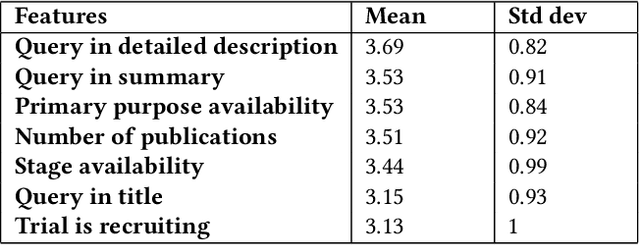
Health care professionals rely on treatment search engines to efficiently find adequate clinical trials and early access programs for their patients. However, doctors lose trust in the system if its underlying processes are unclear and unexplained. In this paper, a model-agnostic explainable method is developed to provide users with further information regarding the reasons why a clinical trial is retrieved in response to a query. To accomplish this, the engine generates features from clinical trials using by using a knowledge graph, clinical trial data and additional medical resources. and a crowd-sourcing methodology is used to determine their importance. Grounded on the proposed methodology, the rationale behind retrieving the clinical trials is explained in layman's terms so that healthcare processionals can effortlessly perceive them. In addition, we compute an explainability score for each of the retrieved items, according to which the items can be ranked. The experiments validated by medical professionals suggest that the proposed methodology induces trust in targeted as well as in non-targeted users, and provide them with reliable explanations and ranking of retrieved items.

An efficient projection neural network for $\ell_1$-regularized logistic regression

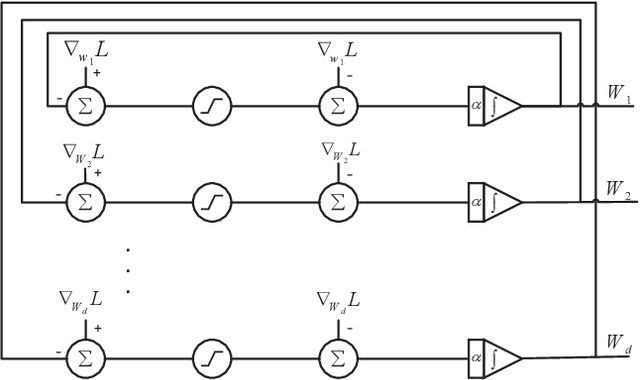
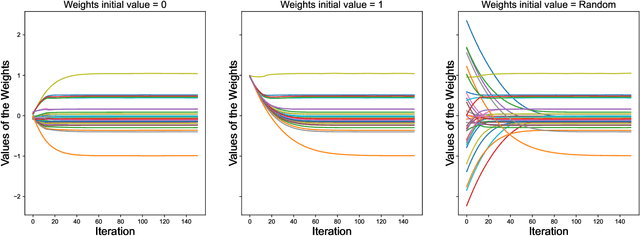
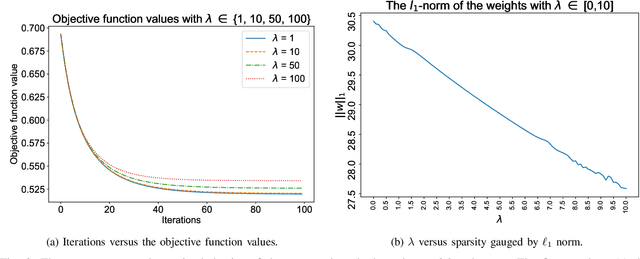
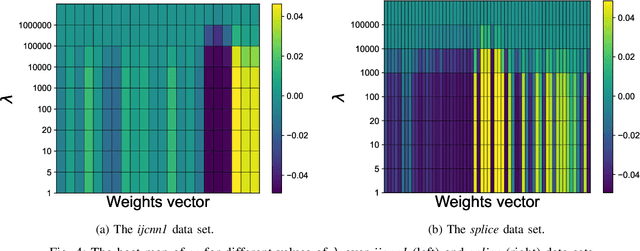
$\ell_1$ regularization has been used for logistic regression to circumvent the overfitting and use the estimated sparse coefficient for feature selection. However, the challenge of such a regularization is that the $\ell_1$ norm is not differentiable, making the standard algorithms for convex optimization not applicable to this problem. This paper presents a simple projection neural network for $\ell_1$-regularized logistics regression. In contrast to many available solvers in the literature, the proposed neural network does not require any extra auxiliary variable nor any smooth approximation, and its complexity is almost identical to that of the gradient descent for logistic regression without $\ell_1$ regularization, thanks to the projection operator. We also investigate the convergence of the proposed neural network by using the Lyapunov theory and show that it converges to a solution of the problem with any arbitrary initial value. The proposed neural solution significantly outperforms state-of-the-art methods with respect to the execution time and is competitive in terms of accuracy and AUROC.

SANOM Results for OAEI 2019

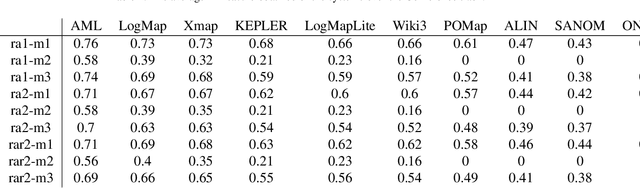
Simulated annealing-based ontology matching (SANOM) participates for the second time at the ontology alignment evaluation initiative (OAEI) 2019. This paper contains the configuration of SANOM and its results on the anatomy and conference tracks. In comparison to the OAEI 2017, SANOM has improved significantly, and its results are competitive with the state-of-the-art systems. In particular, SANOM has the highest recall rate among the participated systems in the conference track, and is competitive with AML, the best performing system, in terms of F-measure. SANOM is also competitive with LogMap on the anatomy track, which is the best performing system in this track with no usage of particular biomedical background knowledge. SANOM has been adapted to the HOBBIT platfrom and is now available for the registered users.

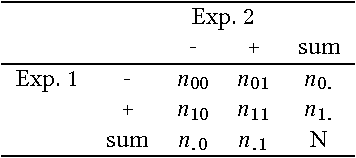
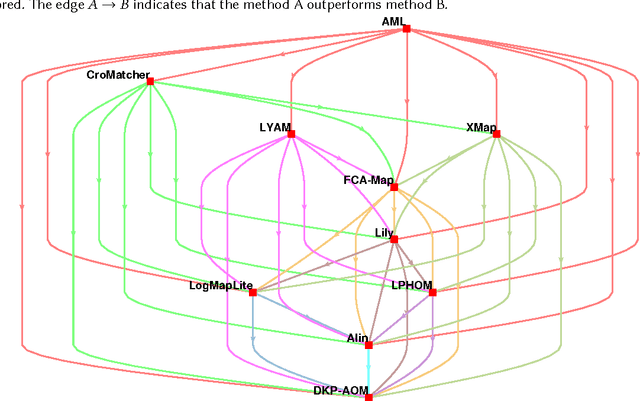
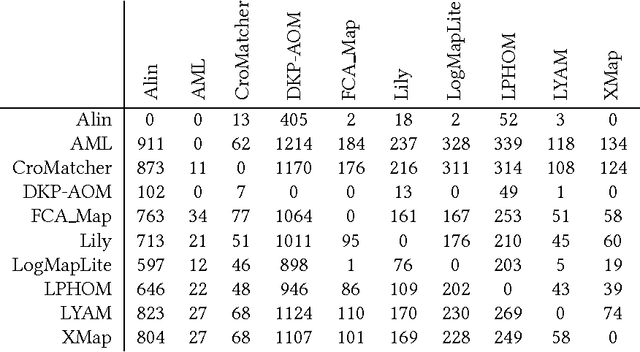
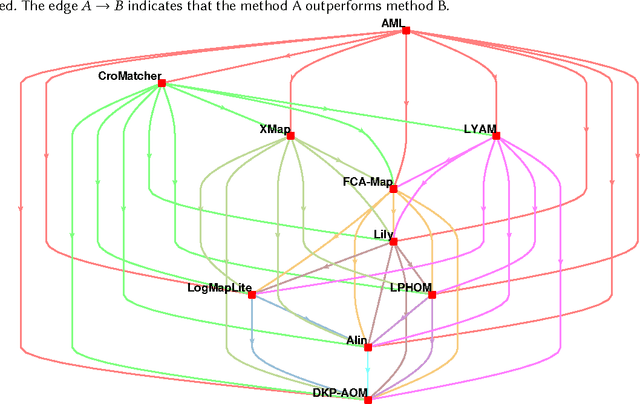
Comparison of ontology alignment systems across single matching task via the McNemar's test

Ontology alignment is widely-used to find the correspondences between different ontologies in diverse fields.After discovering the alignments,several performance scores are available to evaluate them.The scores typically require the identified alignment and a reference containing the underlying actual correspondences of the given ontologies.The current trend in the alignment evaluation is to put forward a new score(e.g., precision, weighted precision, etc.)and to compare various alignments by juxtaposing the obtained scores. However,it is substantially provocative to select one measure among others for comparison.On top of that, claiming if one system has a better performance than one another cannot be substantiated solely by comparing two scalars.In this paper,we propose the statistical procedures which enable us to theoretically favor one system over one another.The McNemar's test is the statistical means by which the comparison of two ontology alignment systems over one matching task is drawn.The test applies to a 2x2 contingency table which can be constructed in two different ways based on the alignments,each of which has their own merits/pitfalls.The ways of the contingency table construction and various apposite statistics from the McNemar's test are elaborated in minute detail.In the case of having more than two alignment systems for comparison, the family-wise error rate is expected to happen. Thus, the ways of preventing such an error are also discussed.A directed graph visualizes the outcome of the McNemar's test in the presence of multiple alignment systems.From this graph, it is readily understood if one system is better than one another or if their differences are imperceptible.The proposed statistical methodologies are applied to the systems participated in the OAEI 2016 anatomy track, and also compares several well-known similarity metrics for the same matching problem.

Solving the L1 regularized least square problem via a box-constrained smooth minimization

In this paper, an equivalent smooth minimization for the L1 regularized least square problem is proposed. The proposed problem is a convex box-constrained smooth minimization which allows applying fast optimization methods to find its solution. Further, it is investigated that the property "the dual of dual is primal" holds for the L1 regularized least square problem. A solver for the smooth problem is proposed, and its affinity to the proximal gradient is shown. Finally, the experiments on L1 and total variation regularized problems are performed, and the corresponding results are reported.