Collaborative AI Teaming in Unknown Environments via Active Goal Deduction

With the advancements of artificial intelligence (AI), we're seeing more scenarios that require AI to work closely with other agents, whose goals and strategies might not be known beforehand. However, existing approaches for training collaborative agents often require defined and known reward signals and cannot address the problem of teaming with unknown agents that often have latent objectives/rewards. In response to this challenge, we propose teaming with unknown agents framework, which leverages kernel density Bayesian inverse learning method for active goal deduction and utilizes pre-trained, goal-conditioned policies to enable zero-shot policy adaptation. We prove that unbiased reward estimates in our framework are sufficient for optimal teaming with unknown agents. We further evaluate the framework of redesigned multi-agent particle and StarCraft II micromanagement environments with diverse unknown agents of different behaviors/rewards. Empirical results demonstrate that our framework significantly advances the teaming performance of AI and unknown agents in a wide range of collaborative scenarios.

Bayesian Optimization through Gaussian Cox Process Models for Spatio-temporal Data

Bayesian optimization (BO) has established itself as a leading strategy for efficiently optimizing expensive-to-evaluate functions. Existing BO methods mostly rely on Gaussian process (GP) surrogate models and are not applicable to (doubly-stochastic) Gaussian Cox processes, where the observation process is modulated by a latent intensity function modeled as a GP. In this paper, we propose a novel maximum a posteriori inference of Gaussian Cox processes. It leverages the Laplace approximation and change of kernel technique to transform the problem into a new reproducing kernel Hilbert space, where it becomes more tractable computationally. It enables us to obtain both a functional posterior of the latent intensity function and the covariance of the posterior, thus extending existing works that often focus on specific link functions or estimating the posterior mean. Using the result, we propose a BO framework based on the Gaussian Cox process model and further develop a Nystr\"om approximation for efficient computation. Extensive evaluations on various synthetic and real-world datasets demonstrate significant improvement over state-of-the-art inference solutions for Gaussian Cox processes, as well as effective BO with a wide range of acquisition functions designed through the underlying Gaussian Cox process model.

A Bayesian Optimization Framework for Finding Local Optima in Expensive Multi-Modal Functions

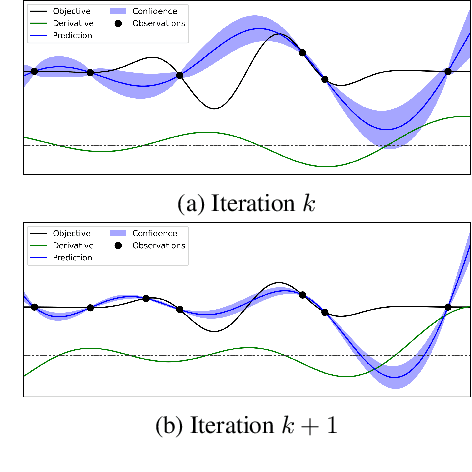
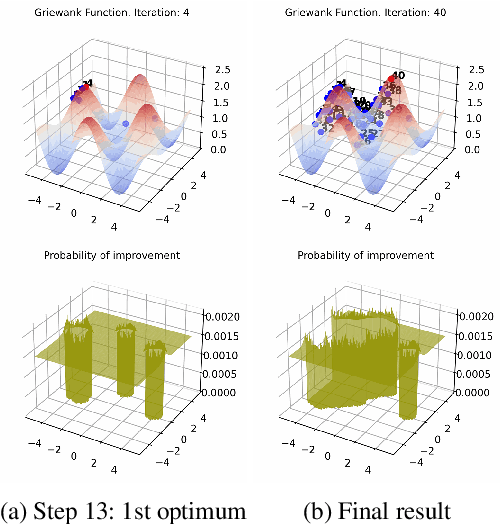
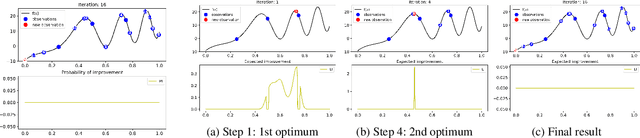
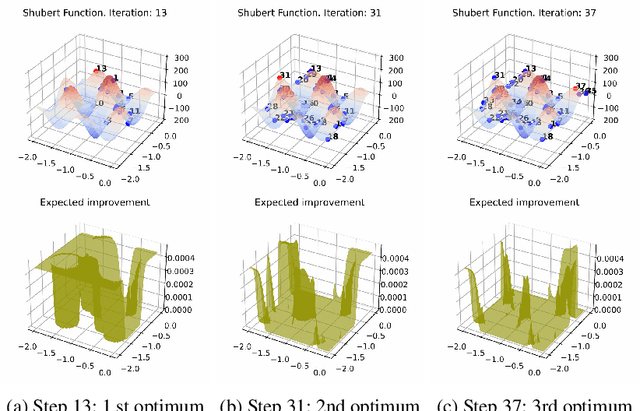
Bayesian optimization (BO) is a popular global optimization scheme for sample-efficient optimization in domains with expensive function evaluations. The existing BO techniques are capable of finding a single global optimum solution. However, finding a set of global and local optimum solutions is crucial in a wide range of real-world problems, as implementing some of the optimal solutions might not be feasible due to various practical restrictions (e.g., resource limitation, physical constraints, etc.). In such domains, if multiple solutions are known, the implementation can be quickly switched to another solution, and the best possible system performance can still be obtained. This paper develops a multi-modal BO framework to effectively find a set of local/global solutions for expensive-to-evaluate multi-modal objective functions. We consider the standard BO setting with Gaussian process regression representing the objective function. We analytically derive the joint distribution of the objective function and its first-order gradients. This joint distribution is used in the body of the BO acquisition functions to search for local optima during the optimization process. We introduce variants of the well-known BO acquisition functions to the multi-modal setting and demonstrate the performance of the proposed framework in locating a set of local optimum solutions using multiple optimization problems.

Inference of Regulatory Networks Through Temporally Sparse Data

A major goal in genomics is to properly capture the complex dynamical behaviors of gene regulatory networks (GRNs). This includes inferring the complex interactions between genes, which can be used for a wide range of genomics analyses, including diagnosis or prognosis of diseases and finding effective treatments for chronic diseases such as cancer. Boolean networks have emerged as a successful class of models for capturing the behavior of GRNs. In most practical settings, inference of GRNs should be achieved through limited and temporally sparse genomics data. A large number of genes in GRNs leads to a large possible topology candidate space, which often cannot be exhaustively searched due to the limitation in computational resources. This paper develops a scalable and efficient topology inference for GRNs using Bayesian optimization and kernel-based methods. Rather than an exhaustive search over possible topologies, the proposed method constructs a Gaussian Process (GP) with a topology-inspired kernel function to account for correlation in the likelihood function. Then, using the posterior distribution of the GP model, the Bayesian optimization efficiently searches for the topology with the highest likelihood value by optimally balancing between exploration and exploitation. The performance of the proposed method is demonstrated through comprehensive numerical experiments using a well-known mammalian cell-cycle network.

Control of Gene Regulatory Networks with Noisy Measurements and Uncertain Inputs

This paper is concerned with the problem of stochastic control of gene regulatory networks (GRNs) observed indirectly through noisy measurements and with uncertainty in the intervention inputs. The partial observability of the gene states and uncertainty in the intervention process are accounted for by modeling GRNs using the partially-observed Boolean dynamical system (POBDS) signal model with noisy gene expression measurements. Obtaining the optimal infinite-horizon control strategy for this problem is not attainable in general, and we apply reinforcement learning and Gaussian process techniques to find a near-optimal solution. The POBDS is first transformed to a directly-observed Markov Decision Process in a continuous belief space, and the Gaussian process is used for modeling the cost function over the belief and intervention spaces. Reinforcement learning then is used to learn the cost function from the available gene expression data. In addition, we employ sparsification, which enables the control of large partially-observed GRNs. The performance of the resulting algorithm is studied through a comprehensive set of numerical experiments using synthetic gene expression data generated from a melanoma gene regulatory network.