FedAuxHMTL: Federated Auxiliary Hard-Parameter Sharing Multi-Task Learning for Network Edge Traffic Classification

Federated Learning (FL) has garnered significant interest recently due to its potential as an effective solution for tackling many challenges in diverse application scenarios, for example, data privacy in network edge traffic classification. Despite its recognized advantages, FL encounters obstacles linked to statistical data heterogeneity and labeled data scarcity during the training of single-task models for machine learning-based traffic classification, leading to hindered learning performance. In response to these challenges, adopting a hard-parameter sharing multi-task learning model with auxiliary tasks proves to be a suitable approach. Such a model has the capability to reduce communication and computation costs, navigate statistical complexities inherent in FL contexts, and overcome labeled data scarcity by leveraging knowledge derived from interconnected auxiliary tasks. This paper introduces a new framework for federated auxiliary hard-parameter sharing multi-task learning, namely, FedAuxHMTL. The introduced framework incorporates model parameter exchanges between edge server and base stations, enabling base stations from distributed areas to participate in the FedAuxHMTL process and enhance the learning performance of the main task-network edge traffic classification. Empirical experiments are conducted to validate and demonstrate the FedAuxHMTL's effectiveness in terms of accuracy, total global loss, communication costs, computing time, and energy consumption compared to its counterparts.

A Bayesian Optimization Framework for Finding Local Optima in Expensive Multi-Modal Functions

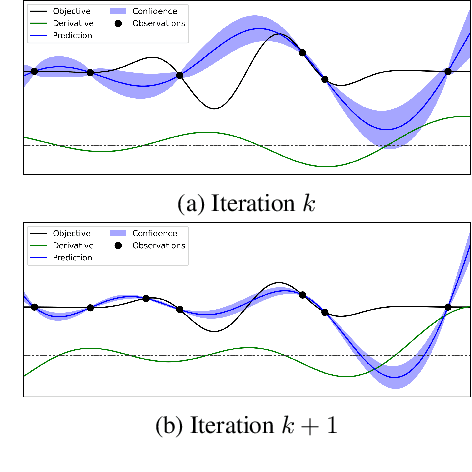
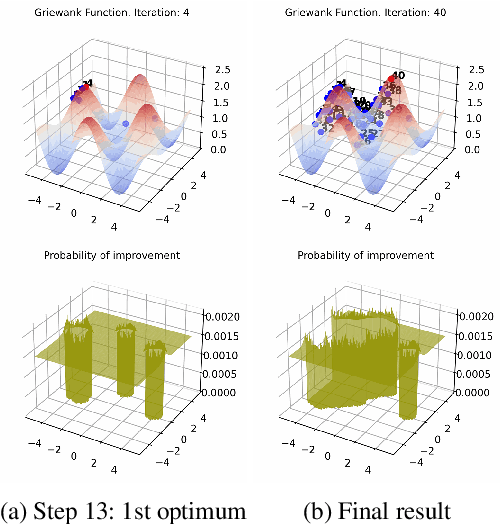
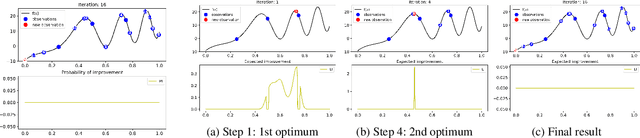
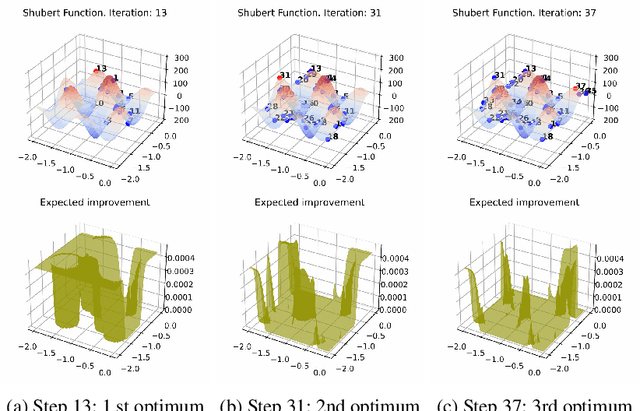
Bayesian optimization (BO) is a popular global optimization scheme for sample-efficient optimization in domains with expensive function evaluations. The existing BO techniques are capable of finding a single global optimum solution. However, finding a set of global and local optimum solutions is crucial in a wide range of real-world problems, as implementing some of the optimal solutions might not be feasible due to various practical restrictions (e.g., resource limitation, physical constraints, etc.). In such domains, if multiple solutions are known, the implementation can be quickly switched to another solution, and the best possible system performance can still be obtained. This paper develops a multi-modal BO framework to effectively find a set of local/global solutions for expensive-to-evaluate multi-modal objective functions. We consider the standard BO setting with Gaussian process regression representing the objective function. We analytically derive the joint distribution of the objective function and its first-order gradients. This joint distribution is used in the body of the BO acquisition functions to search for local optima during the optimization process. We introduce variants of the well-known BO acquisition functions to the multi-modal setting and demonstrate the performance of the proposed framework in locating a set of local optimum solutions using multiple optimization problems.