A Bayesian Optimization Framework for Finding Local Optima in Expensive Multi-Modal Functions

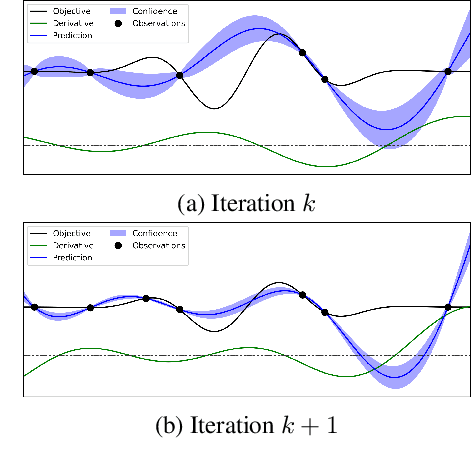
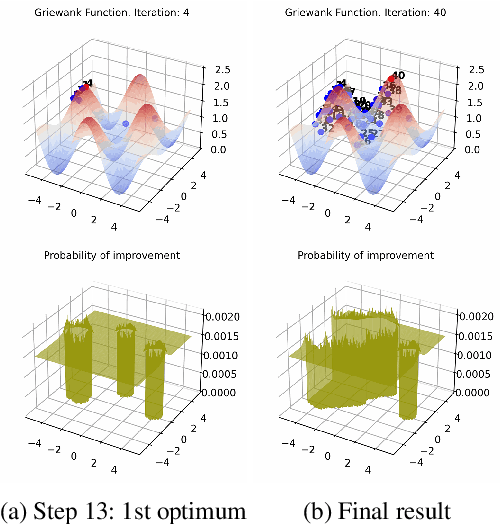
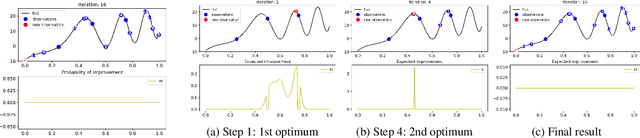
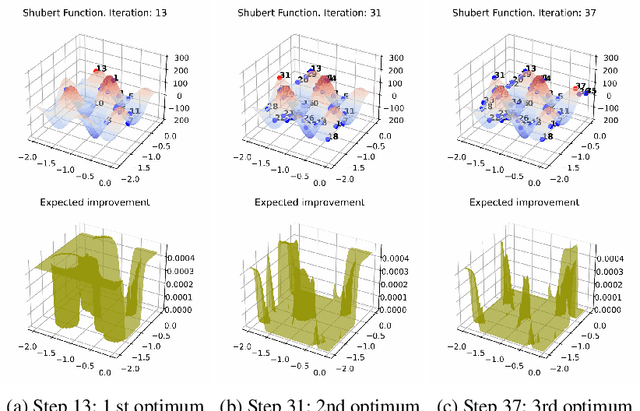
Bayesian optimization (BO) is a popular global optimization scheme for sample-efficient optimization in domains with expensive function evaluations. The existing BO techniques are capable of finding a single global optimum solution. However, finding a set of global and local optimum solutions is crucial in a wide range of real-world problems, as implementing some of the optimal solutions might not be feasible due to various practical restrictions (e.g., resource limitation, physical constraints, etc.). In such domains, if multiple solutions are known, the implementation can be quickly switched to another solution, and the best possible system performance can still be obtained. This paper develops a multi-modal BO framework to effectively find a set of local/global solutions for expensive-to-evaluate multi-modal objective functions. We consider the standard BO setting with Gaussian process regression representing the objective function. We analytically derive the joint distribution of the objective function and its first-order gradients. This joint distribution is used in the body of the BO acquisition functions to search for local optima during the optimization process. We introduce variants of the well-known BO acquisition functions to the multi-modal setting and demonstrate the performance of the proposed framework in locating a set of local optimum solutions using multiple optimization problems.