Inference of Regulatory Networks Through Temporally Sparse Data
Paper and Code
Jul 21, 2022


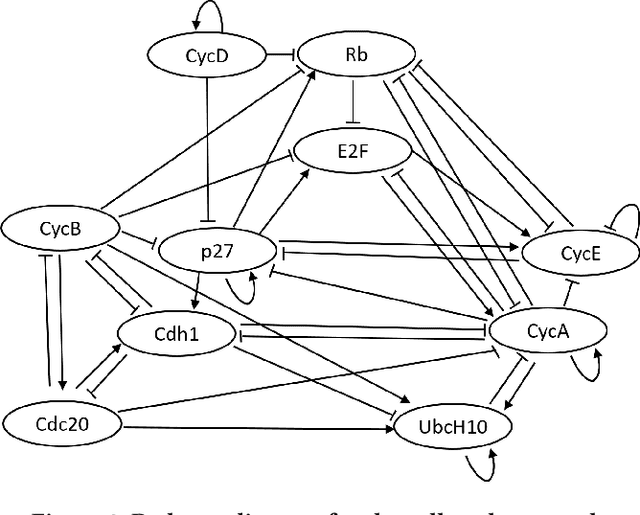
A major goal in genomics is to properly capture the complex dynamical behaviors of gene regulatory networks (GRNs). This includes inferring the complex interactions between genes, which can be used for a wide range of genomics analyses, including diagnosis or prognosis of diseases and finding effective treatments for chronic diseases such as cancer. Boolean networks have emerged as a successful class of models for capturing the behavior of GRNs. In most practical settings, inference of GRNs should be achieved through limited and temporally sparse genomics data. A large number of genes in GRNs leads to a large possible topology candidate space, which often cannot be exhaustively searched due to the limitation in computational resources. This paper develops a scalable and efficient topology inference for GRNs using Bayesian optimization and kernel-based methods. Rather than an exhaustive search over possible topologies, the proposed method constructs a Gaussian Process (GP) with a topology-inspired kernel function to account for correlation in the likelihood function. Then, using the posterior distribution of the GP model, the Bayesian optimization efficiently searches for the topology with the highest likelihood value by optimally balancing between exploration and exploitation. The performance of the proposed method is demonstrated through comprehensive numerical experiments using a well-known mammalian cell-cycle network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge