A Systematic Study of Multi-Agent Deep Reinforcement Learning for Safe and Robust Autonomous Highway Ramp Entry

Vehicles today can drive themselves on highways and driverless robotaxis operate in major cities, with more sophisticated levels of autonomous driving expected to be available and become more common in the future. Yet, technically speaking, so-called "Level 5" (L5) operation, corresponding to full autonomy, has not been achieved. For that to happen, functions such as fully autonomous highway ramp entry must be available, and provide provably safe, and reliably robust behavior to enable full autonomy. We present a systematic study of a highway ramp function that controls the vehicles forward-moving actions to minimize collisions with the stream of highway traffic into which a merging (ego) vehicle enters. We take a game-theoretic multi-agent (MA) approach to this problem and study the use of controllers based on deep reinforcement learning (DRL). The virtual environment of the MA DRL uses self-play with simulated data where merging vehicles safely learn to control longitudinal position during a taper-type merge. The work presented in this paper extends existing work by studying the interaction of more than two vehicles (agents) and does so by systematically expanding the road scene with additional traffic and ego vehicles. While previous work on the two-vehicle setting established that collision-free controllers are theoretically impossible in fully decentralized, non-coordinated environments, we empirically show that controllers learned using our approach are nearly ideal when measured against idealized optimal controllers.

Correlated Equilibria for Approximate Variational Inference in MRFs

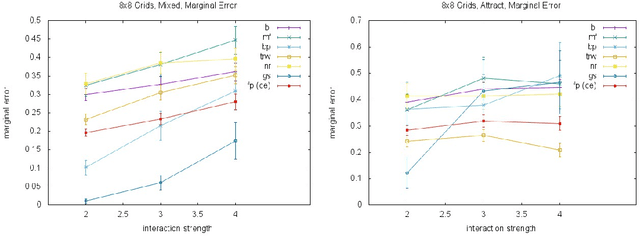
Almost all of the work in graphical models for game theory has mirrored previous work in probabilistic graphical models. Our work considers the opposite direction: Taking advantage of recent advances in equilibrium computation for probabilistic inference. We present formulations of inference problems in Markov random fields (MRFs) as computation of equilibria in a certain class of game-theoretic graphical models. We concretely establishes the precise connection between variational probabilistic inference in MRFs and correlated equilibria. No previous work exploits recent theoretical and empirical results from the literature on algorithmic and computational game theory on the tractable, polynomial-time computation of exact or approximate correlated equilibria in graphical games with arbitrary, loopy graph structure. We discuss how to design new algorithms with equally tractable guarantees for the computation of approximate variational inference in MRFs. Also, inspired by a previously stated game-theoretic view of state-of-the-art tree-reweighed (TRW) message-passing techniques for belief inference as zero-sum game, we propose a different, general-sum potential game to design approximate fictitious-play techniques. We perform synthetic experiments evaluating our proposed approximation algorithms with standard methods and TRW on several classes of classical Ising models (i.e., with binary random variables). We also evaluate the algorithms using Ising models learned from the MNIST dataset. Our experiments show that our global approach is competitive, particularly shinning in a class of Ising models with constant, "highly attractive" edge-weights, in which it is often better than all other alternatives we evaluated. With a notable exception, our more local approach was not as effective. Yet, in fairness, almost all of the alternatives are often no better than a simple baseline: estimate 0.5.

Some Open Problems in Optimal AdaBoost and Decision Stumps

The significance of the study of the theoretical and practical properties of AdaBoost is unquestionable, given its simplicity, wide practical use, and effectiveness on real-world datasets. Here we present a few open problems regarding the behavior of "Optimal AdaBoost," a term coined by Rudin, Daubechies, and Schapire in 2004 to label the simple version of the standard AdaBoost algorithm in which the weak learner that AdaBoost uses always outputs the weak classifier with lowest weighted error among the respective hypothesis class of weak classifiers implicit in the weak learner. We concentrate on the standard, "vanilla" version of Optimal AdaBoost for binary classification that results from using an exponential-loss upper bound on the misclassification training error. We present two types of open problems. One deals with general weak hypotheses. The other deals with the particular case of decision stumps, as often and commonly used in practice. Answers to the open problems can have immediate significant impact to (1) cementing previously established results on asymptotic convergence properties of Optimal AdaBoost, for finite datasets, which in turn can be the start to any convergence-rate analysis; (2) understanding the weak-hypotheses class of effective decision stumps generated from data, which we have empirically observed to be significantly smaller than the typically obtained class, as well as the effect on the weak learner's running time and previously established improved bounds on the generalization performance of Optimal AdaBoost classifiers; and (3) shedding some light on the "self control" that AdaBoost tends to exhibit in practice.

Graphical Potential Games

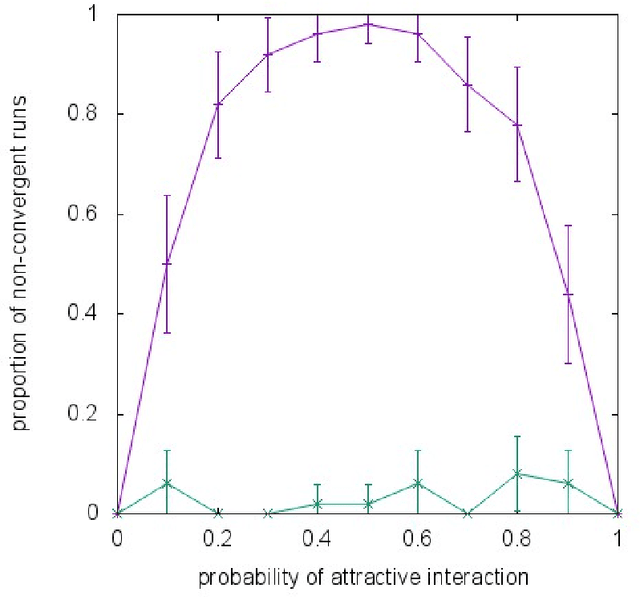
Potential games, originally introduced in the early 1990's by Lloyd Shapley, the 2012 Nobel Laureate in Economics, and his colleague Dov Monderer, are a very important class of models in game theory. They have special properties such as the existence of Nash equilibria in pure strategies. This note introduces graphical versions of potential games. Special cases of graphical potential games have already found applicability in many areas of science and engineering beyond economics, including artificial intelligence, computer vision, and machine learning. They have been effectively applied to the study and solution of important real-world problems such as routing and congestion in networks, distributed resource allocation (e.g., public goods), and relaxation-labeling for image segmentation. Implicit use of graphical potential games goes back at least 40 years. Several classes of games considered standard in the literature, including coordination games, local interaction games, lattice games, congestion games, and party-affiliation games, are instances of graphical potential games. This note provides several characterizations of graphical potential games by leveraging well-known results from the literature on probabilistic graphical models. A major contribution of the work presented here that particularly distinguishes it from previous work is establishing that the convergence of certain type of game-playing rules implies that the agents/players must be embedded in some graphical potential game.

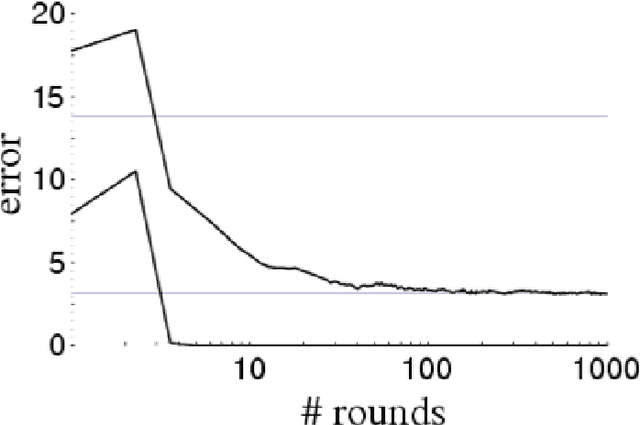
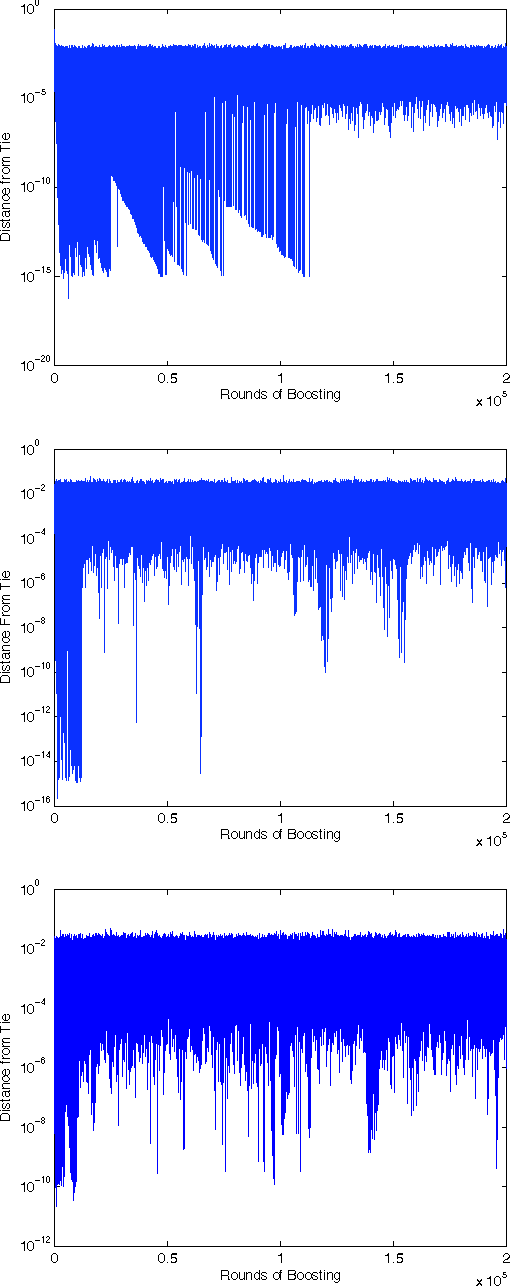
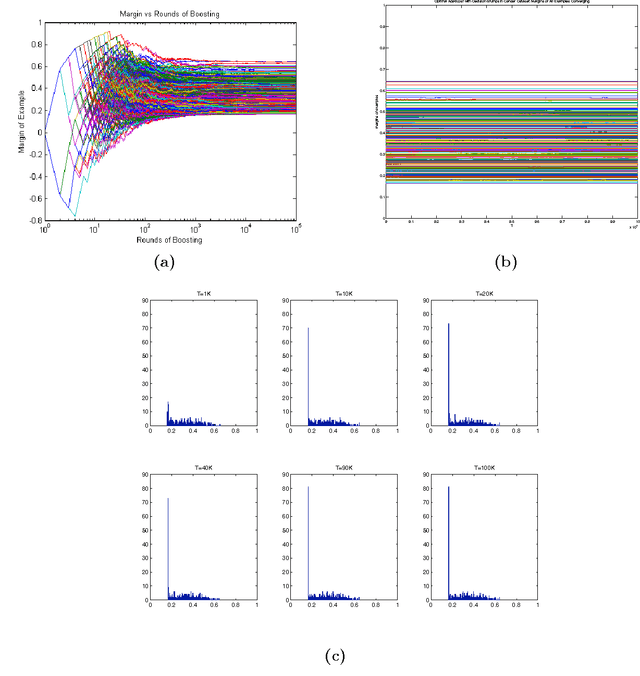
On the Convergence Properties of Optimal AdaBoost

AdaBoost is one of the most popular machine-learning algorithms. It is simple to implement and often found very effective by practitioners, while still being mathematically elegant and theoretically sound. AdaBoost's behavior in practice, and in particular the test-error behavior, has puzzled many eminent researchers for over a decade: It seems to defy our general intuition in machine learning regarding the fundamental trade-off between model complexity and generalization performance. In this paper, we establish the convergence of "Optimal AdaBoost," a term coined by Rudin, Daubechies, and Schapire in 2004. We prove the convergence, with the number of rounds, of the classifier itself, its generalization error, and its resulting margins for fixed data sets, under certain reasonable conditions. More generally, we prove that the time/per-round average of almost any function of the example weights converges. Our approach is to frame AdaBoost as a dynamical system, to provide sufficient conditions for the existence of an invariant measure, and to employ tools from ergodic theory. Unlike previous work, we do not assume AdaBoost cycles; actually, we present empirical evidence against it on real-world datasets. Our main theoretical results hold under a weaker condition. We show sufficient empirical evidence that Optimal AdaBoost always met the condition on every real-world dataset we tried. Our results formally ground future convergence-rate analyses, and may even provide opportunities for slight algorithmic modifications to optimize the generalization ability of AdaBoost classifiers, thus reducing a practitioner's burden of deciding how long to run the algorithm.

On Sparse Discretization for Graphical Games

This short paper concerns discretization schemes for representing and computing approximate Nash equilibria, with emphasis on graphical games, but briefly touching on normal-form and poly-matrix games. The main technical contribution is a representation theorem that informally states that to account for every exact Nash equilibrium using a nearby approximate Nash equilibrium on a grid over mixed strategies, a uniform discretization size linear on the inverse of the approximation quality and natural game-representation parameters suffices. For graphical games, under natural conditions, the discretization is logarithmic in the game-representation size, a substantial improvement over the linear dependency previously required. The paper has five other objectives: (1) given the venue, to highlight the important, but often ignored, role that work on constraint networks in AI has in simplifying the derivation and analysis of algorithms for computing approximate Nash equilibria; (2) to summarize the state-of-the-art on computing approximate Nash equilibria, with emphasis on relevance to graphical games; (3) to help clarify the distinction between sparse-discretization and sparse-support techniques; (4) to illustrate and advocate for the deliberate mathematical simplicity of the formal proof of the representation theorem; and (5) to list and discuss important open problems, emphasizing graphical-game generalizations, which the AI community is most suitable to solve.

Accelerating EM: An Empirical Study

Many applications require that we learn the parameters of a model from data. EM is a method used to learn the parameters of probabilistic models for which the data for some of the variables in the models is either missing or hidden. There are instances in which this method is slow to converge. Therefore, several accelerations have been proposed to improve the method. None of the proposed acceleration methods are theoretically dominant and experimental comparisons are lacking. In this paper, we present the different proposed accelerations and try to compare them experimentally. From the results of the experiments, we argue that some acceleration of EM is always possible, but that which acceleration is superior depends on properties of the problem.

Adaptive Importance Sampling for Estimation in Structured Domains

Sampling is an important tool for estimating large, complex sums and integrals over high dimensional spaces. For instance, important sampling has been used as an alternative to exact methods for inference in belief networks. Ideally, we want to have a sampling distribution that provides optimal-variance estimators. In this paper, we present methods that improve the sampling distribution by systematically adapting it as we obtain information from the samples. We present a stochastic-gradient-descent method for sequentially updating the sampling distribution based on the direct minization of the variance. We also present other stochastic-gradient-descent methods based on the minimizationof typical notions of distance between the current sampling distribution and approximations of the target, optimal distribution. We finally validate and compare the different methods empirically by applying them to the problem of action evaluation in influence diagrams.

Value-Directed Sampling Methods for POMDPs

We consider the problem of approximate belief-state monitoring using particle filtering for the purposes of implementing a policy for a partially-observable Markov decision process (POMDP). While particle filtering has become a widely-used tool in AI for monitoring dynamical systems, rather scant attention has been paid to their use in the context of decision making. Assuming the existence of a value function, we derive error bounds on decision quality associated with filtering using importance sampling. We also describe an adaptive procedure that can be used to dynamically determine the number of samples required to meet specific error bounds. Empirical evidence is offered supporting this technique as a profitable means of directing sampling effort where it is needed to distinguish policies.