Some Open Problems in Optimal AdaBoost and Decision Stumps

The significance of the study of the theoretical and practical properties of AdaBoost is unquestionable, given its simplicity, wide practical use, and effectiveness on real-world datasets. Here we present a few open problems regarding the behavior of "Optimal AdaBoost," a term coined by Rudin, Daubechies, and Schapire in 2004 to label the simple version of the standard AdaBoost algorithm in which the weak learner that AdaBoost uses always outputs the weak classifier with lowest weighted error among the respective hypothesis class of weak classifiers implicit in the weak learner. We concentrate on the standard, "vanilla" version of Optimal AdaBoost for binary classification that results from using an exponential-loss upper bound on the misclassification training error. We present two types of open problems. One deals with general weak hypotheses. The other deals with the particular case of decision stumps, as often and commonly used in practice. Answers to the open problems can have immediate significant impact to (1) cementing previously established results on asymptotic convergence properties of Optimal AdaBoost, for finite datasets, which in turn can be the start to any convergence-rate analysis; (2) understanding the weak-hypotheses class of effective decision stumps generated from data, which we have empirically observed to be significantly smaller than the typically obtained class, as well as the effect on the weak learner's running time and previously established improved bounds on the generalization performance of Optimal AdaBoost classifiers; and (3) shedding some light on the "self control" that AdaBoost tends to exhibit in practice.

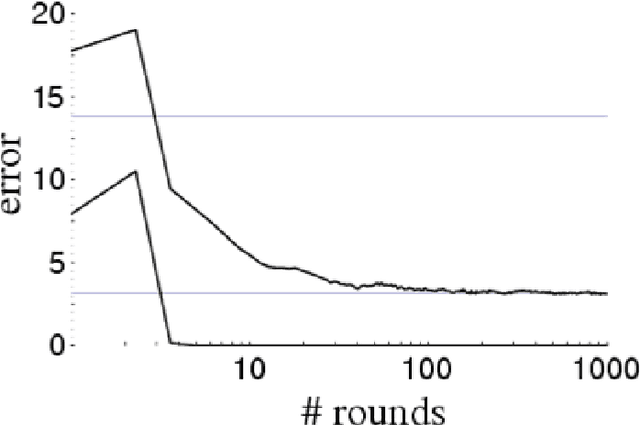
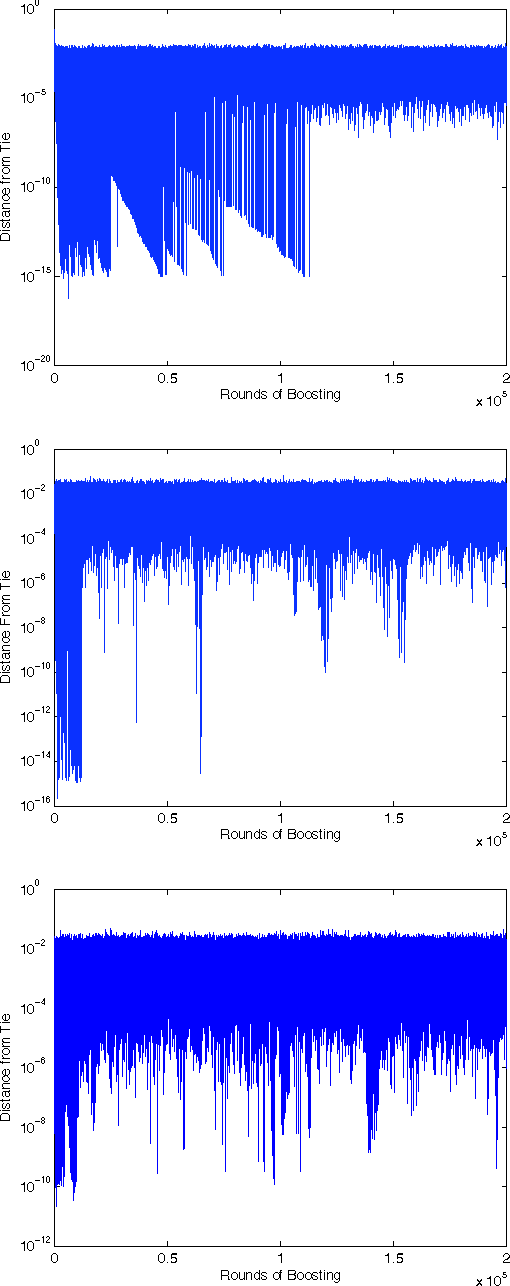
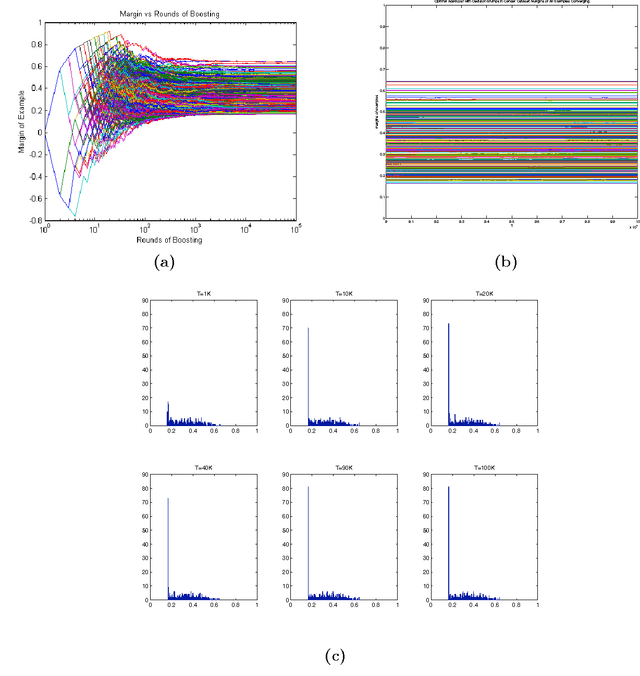
On the Convergence Properties of Optimal AdaBoost

AdaBoost is one of the most popular machine-learning algorithms. It is simple to implement and often found very effective by practitioners, while still being mathematically elegant and theoretically sound. AdaBoost's behavior in practice, and in particular the test-error behavior, has puzzled many eminent researchers for over a decade: It seems to defy our general intuition in machine learning regarding the fundamental trade-off between model complexity and generalization performance. In this paper, we establish the convergence of "Optimal AdaBoost," a term coined by Rudin, Daubechies, and Schapire in 2004. We prove the convergence, with the number of rounds, of the classifier itself, its generalization error, and its resulting margins for fixed data sets, under certain reasonable conditions. More generally, we prove that the time/per-round average of almost any function of the example weights converges. Our approach is to frame AdaBoost as a dynamical system, to provide sufficient conditions for the existence of an invariant measure, and to employ tools from ergodic theory. Unlike previous work, we do not assume AdaBoost cycles; actually, we present empirical evidence against it on real-world datasets. Our main theoretical results hold under a weaker condition. We show sufficient empirical evidence that Optimal AdaBoost always met the condition on every real-world dataset we tried. Our results formally ground future convergence-rate analyses, and may even provide opportunities for slight algorithmic modifications to optimize the generalization ability of AdaBoost classifiers, thus reducing a practitioner's burden of deciding how long to run the algorithm.