On the Convergence Properties of Optimal AdaBoost

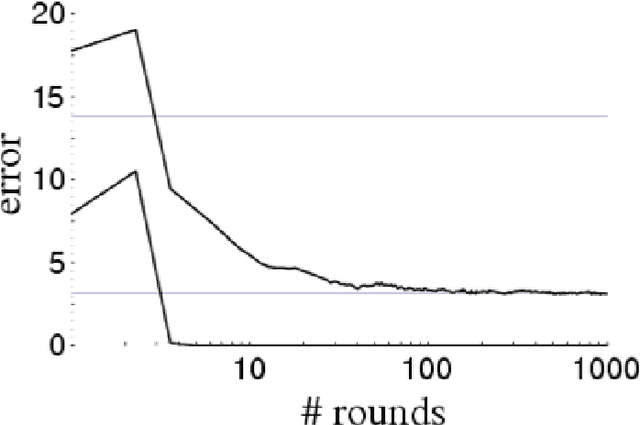
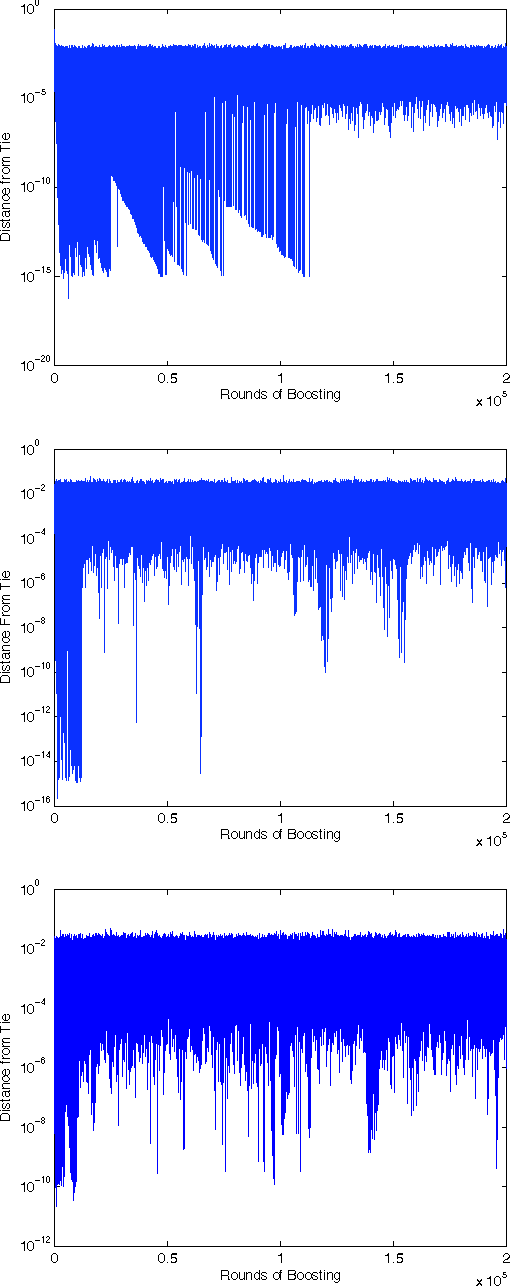
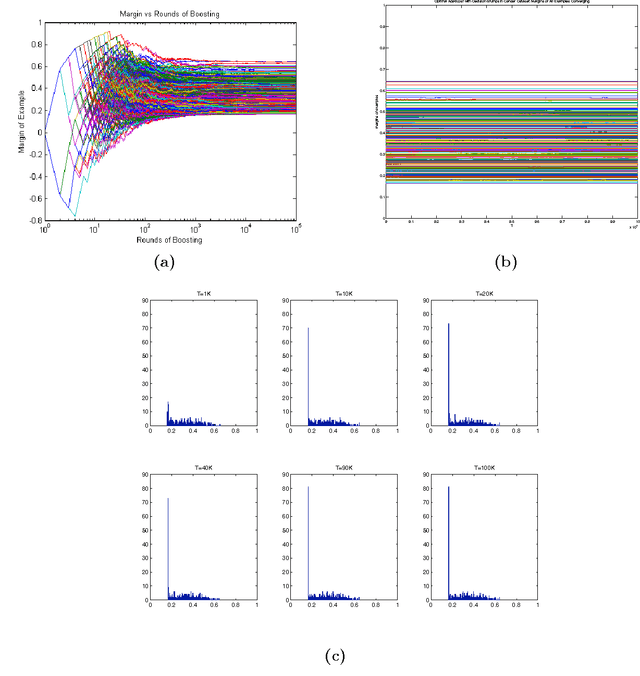
AdaBoost is one of the most popular machine-learning algorithms. It is simple to implement and often found very effective by practitioners, while still being mathematically elegant and theoretically sound. AdaBoost's behavior in practice, and in particular the test-error behavior, has puzzled many eminent researchers for over a decade: It seems to defy our general intuition in machine learning regarding the fundamental trade-off between model complexity and generalization performance. In this paper, we establish the convergence of "Optimal AdaBoost," a term coined by Rudin, Daubechies, and Schapire in 2004. We prove the convergence, with the number of rounds, of the classifier itself, its generalization error, and its resulting margins for fixed data sets, under certain reasonable conditions. More generally, we prove that the time/per-round average of almost any function of the example weights converges. Our approach is to frame AdaBoost as a dynamical system, to provide sufficient conditions for the existence of an invariant measure, and to employ tools from ergodic theory. Unlike previous work, we do not assume AdaBoost cycles; actually, we present empirical evidence against it on real-world datasets. Our main theoretical results hold under a weaker condition. We show sufficient empirical evidence that Optimal AdaBoost always met the condition on every real-world dataset we tried. Our results formally ground future convergence-rate analyses, and may even provide opportunities for slight algorithmic modifications to optimize the generalization ability of AdaBoost classifiers, thus reducing a practitioner's burden of deciding how long to run the algorithm.