ALPHAGMUT: A Rationale-Guided Alpha Shape Graph Neural Network to Evaluate Mutation Effects

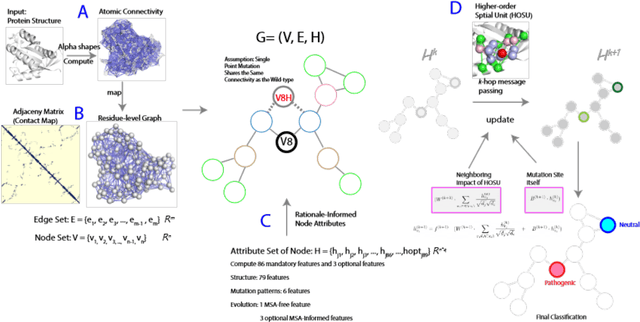
In silico methods evaluating the mutation effects of missense mutations are providing an important approach for understanding mutations in personal genomes and identifying disease-relevant biomarkers. However, existing methods, including deep learning methods, heavily rely on sequence-aware information, and do not fully leverage the potential of available 3D structural information. In addition, these methods may exhibit an inability to predict mutations in domains difficult to formulate sequence-based embeddings. In this study, we introduce a novel rationale-guided graph neural network AlphaGMut to evaluate mutation effects and to distinguish pathogenic mutations from neutral mutations. We compute the alpha shapes of protein structures to obtain atomic-resolution edge connectivities and map them to an accurate residue-level graph representation. We then compute structural-, topological-, biophysical-, and sequence properties of the mutation sites, which are assigned as node attributes in the graph. These node attributes could effectively guide the graph neural network to learn the difference between pathogenic and neutral mutations using k-hop message passing with a short training period. We demonstrate that AlphaGMut outperforms state-of-the-art methods, including DeepMind's AlphaMissense, in many performance metrics. In addition, AlphaGMut has the advantage of performing well in alignment-free settings, which provides broader prediction coverage and better generalization compared to current methods requiring deep sequence-aware information.

Correlated Equilibria for Approximate Variational Inference in MRFs

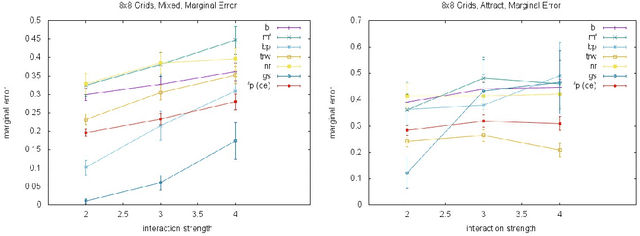
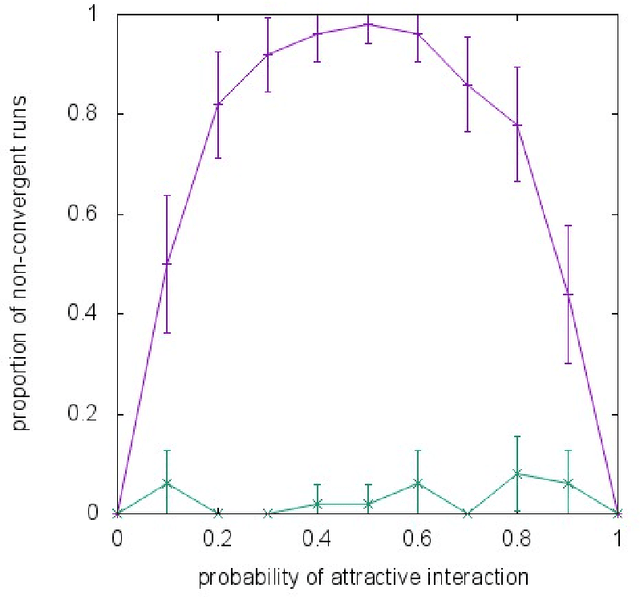
Almost all of the work in graphical models for game theory has mirrored previous work in probabilistic graphical models. Our work considers the opposite direction: Taking advantage of recent advances in equilibrium computation for probabilistic inference. We present formulations of inference problems in Markov random fields (MRFs) as computation of equilibria in a certain class of game-theoretic graphical models. We concretely establishes the precise connection between variational probabilistic inference in MRFs and correlated equilibria. No previous work exploits recent theoretical and empirical results from the literature on algorithmic and computational game theory on the tractable, polynomial-time computation of exact or approximate correlated equilibria in graphical games with arbitrary, loopy graph structure. We discuss how to design new algorithms with equally tractable guarantees for the computation of approximate variational inference in MRFs. Also, inspired by a previously stated game-theoretic view of state-of-the-art tree-reweighed (TRW) message-passing techniques for belief inference as zero-sum game, we propose a different, general-sum potential game to design approximate fictitious-play techniques. We perform synthetic experiments evaluating our proposed approximation algorithms with standard methods and TRW on several classes of classical Ising models (i.e., with binary random variables). We also evaluate the algorithms using Ising models learned from the MNIST dataset. Our experiments show that our global approach is competitive, particularly shinning in a class of Ising models with constant, "highly attractive" edge-weights, in which it is often better than all other alternatives we evaluated. With a notable exception, our more local approach was not as effective. Yet, in fairness, almost all of the alternatives are often no better than a simple baseline: estimate 0.5.