Correlated Equilibria for Approximate Variational Inference in MRFs
Paper and Code
Oct 07, 2017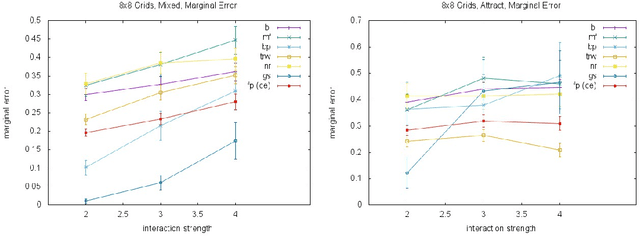

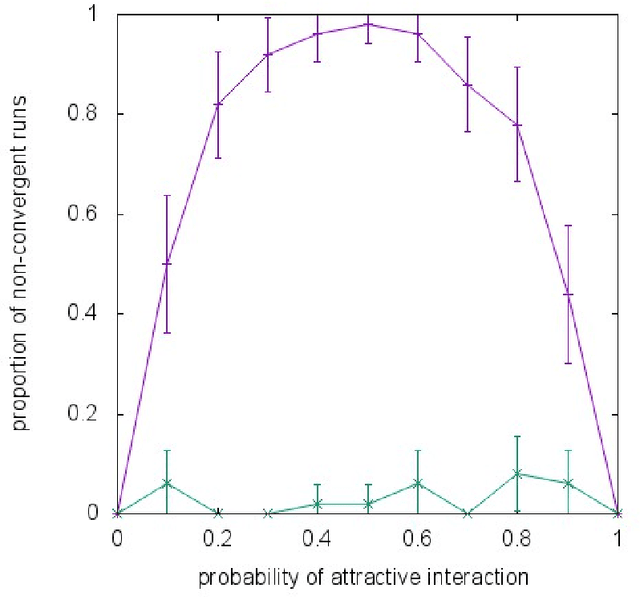
Almost all of the work in graphical models for game theory has mirrored previous work in probabilistic graphical models. Our work considers the opposite direction: Taking advantage of recent advances in equilibrium computation for probabilistic inference. We present formulations of inference problems in Markov random fields (MRFs) as computation of equilibria in a certain class of game-theoretic graphical models. We concretely establishes the precise connection between variational probabilistic inference in MRFs and correlated equilibria. No previous work exploits recent theoretical and empirical results from the literature on algorithmic and computational game theory on the tractable, polynomial-time computation of exact or approximate correlated equilibria in graphical games with arbitrary, loopy graph structure. We discuss how to design new algorithms with equally tractable guarantees for the computation of approximate variational inference in MRFs. Also, inspired by a previously stated game-theoretic view of state-of-the-art tree-reweighed (TRW) message-passing techniques for belief inference as zero-sum game, we propose a different, general-sum potential game to design approximate fictitious-play techniques. We perform synthetic experiments evaluating our proposed approximation algorithms with standard methods and TRW on several classes of classical Ising models (i.e., with binary random variables). We also evaluate the algorithms using Ising models learned from the MNIST dataset. Our experiments show that our global approach is competitive, particularly shinning in a class of Ising models with constant, "highly attractive" edge-weights, in which it is often better than all other alternatives we evaluated. With a notable exception, our more local approach was not as effective. Yet, in fairness, almost all of the alternatives are often no better than a simple baseline: estimate 0.5.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge