Improving Adaptive Moment Optimization via Preconditioner Diagonalization

Modern adaptive optimization methods, such as Adam and its variants, have emerged as the most widely used tools in deep learning over recent years. These algorithms offer automatic mechanisms for dynamically adjusting the update step based on estimates of gradient statistics. Compared to traditional algorithms like Stochastic Gradient Descent, these adaptive methods are typically more robust to model scale and hyperparameter tuning. However, the gradient statistics employed by these methods often do not leverage sufficient gradient covariance information, leading to suboptimal updates in certain directions of the parameter space and potentially slower convergence. In this work, we keep track of such covariance statistics in the form of a structured preconditioner matrix. Unlike other works, our approach does not apply direct approximations to estimate this matrix. We instead implement an invertible transformation that maps the preconditioner matrix into a new space where it becomes approximately diagonal. This enables a diagonal approximation of the preconditioner matrix in the transformed space, offering several computational advantages. Empirical results show that our approach can substantially enhance the convergence speed of modern adaptive optimizers. Notably, for large language models like LLaMA, we can achieve a speedup of 2x compared to the baseline Adam. Additionally, our method can be integrated with memory-efficient optimizers like Adafactor to manage computational overhead.

Cautious Optimizers: Improving Training with One Line of Code

AdamW has been the default optimizer for transformer pretraining. For many years, our community searches for faster and more stable optimizers with only constraint positive outcomes. In this work, we propose a \textbf{single-line modification in Pytorch} to any momentum-based optimizer, which we rename Cautious Optimizer, e.g. C-AdamW and C-Lion. Our theoretical result shows that this modification preserves Adam's Hamiltonian function and it does not break the convergence guarantee under the Lyapunov analysis. In addition, a whole new family of optimizers is revealed by our theoretical insight. Among them, we pick the simplest one for empirical experiments, showing speed-up on Llama and MAE pretraining up to $1.47\times$. Code is available at https://github.com/kyleliang919/C-Optim

Memory-Efficient LLM Training with Online Subspace Descent

Recently, a wide range of memory-efficient LLM training algorithms have gained substantial popularity. These methods leverage the low-rank structure of gradients to project optimizer states into a subspace using projection matrix found by singular value decomposition (SVD). However, convergence of these algorithms is highly dependent on the update rules of their projection matrix. In this work, we provide the \emph{first} convergence guarantee for arbitrary update rules of projection matrix. This guarantee is generally applicable to optimizers that can be analyzed with Hamiltonian Descent, including most common ones, such as LION, Adam. Inspired by our theoretical understanding, we propose Online Subspace Descent, a new family of subspace descent optimizer without SVD. Instead of updating the projection matrix with eigenvectors, Online Subspace Descent updates the projection matrix with online PCA. Online Subspace Descent is flexible and introduces only minimum overhead to training. We show that for the task of pretraining LLaMA models ranging from 60M to 7B parameters on the C4 dataset, Online Subspace Descent achieves lower perplexity and better downstream tasks performance than state-of-the-art low-rank training methods across different settings and narrows the gap with full-rank baselines.

H-Fac: Memory-Efficient Optimization with Factorized Hamiltonian Descent

In this study, we introduce a novel adaptive optimizer, H-Fac, which incorporates a factorized approach to momentum and scaling parameters. Our algorithm demonstrates competitive performances on both ResNets and Vision Transformers, while achieving sublinear memory costs through the use of rank-1 parameterizations for moment estimators. We develop our algorithms based on principles derived from Hamiltonian dynamics, providing robust theoretical underpinnings. These optimization algorithms are designed to be both straightforward and adaptable, facilitating easy implementation in diverse settings.

Communication Efficient Distributed Training with Distributed Lion

The Lion optimizer has been a promising competitor with the AdamW for training large AI models, with advantages on memory, computation, and sample efficiency. In this paper, we introduce Distributed Lion, an innovative adaptation of Lion for distributed training environments. Leveraging the sign operator in Lion, our Distributed Lion only requires communicating binary or lower-precision vectors between workers to the center server, significantly reducing the communication cost. Our theoretical analysis confirms Distributed Lion's convergence properties. Empirical results demonstrate its robustness across a range of tasks, worker counts, and batch sizes, on both vision and language problems. Notably, Distributed Lion attains comparable performance to standard Lion or AdamW optimizers applied on aggregated gradients, but with significantly reduced communication bandwidth. This feature is particularly advantageous for training large models. In addition, we also demonstrate that Distributed Lion presents a more favorable performance-bandwidth balance compared to existing efficient distributed methods such as deep gradient compression and ternary gradients.

Lion Secretly Solves Constrained Optimization: As Lyapunov Predicts

Lion (Evolved Sign Momentum), a new optimizer discovered through program search, has shown promising results in training large AI models. It performs comparably or favorably to AdamW but with greater memory efficiency. As we can expect from the results of a random search program, Lion incorporates elements from several existing algorithms, including signed momentum, decoupled weight decay, Polak, and Nesterov momentum, but does not fit into any existing category of theoretically grounded optimizers. Thus, even though Lion appears to perform well as a general-purpose optimizer for a wide range of tasks, its theoretical basis remains uncertain. This lack of theoretical clarity limits opportunities to further enhance and expand Lion's efficacy. This work aims to demystify Lion. Based on both continuous-time and discrete-time analysis, we demonstrate that Lion is a theoretically novel and principled approach for minimizing a general loss function $f(x)$ while enforcing a bound constraint $\|x\|_\infty \leq 1/\lambda$. Lion achieves this through the incorporation of decoupled weight decay, where $\lambda$ represents the weight decay coefficient. Our analysis is made possible by the development of a new Lyapunov function for the Lion updates. It applies to a broader family of Lion-$\kappa$ algorithms, where the $\text{sign}(\cdot)$ operator in Lion is replaced by the subgradient of a convex function $\kappa$, leading to the solution of a general composite optimization problem of $\min_x f(x) + \kappa^*(x)$. Our findings provide valuable insights into the dynamics of Lion and pave the way for further improvements and extensions of Lion-related algorithms.

An Experimental Study of Semantic Continuity for Deep Learning Models

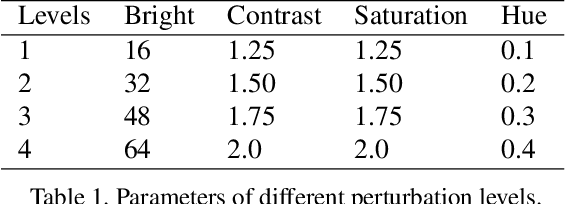
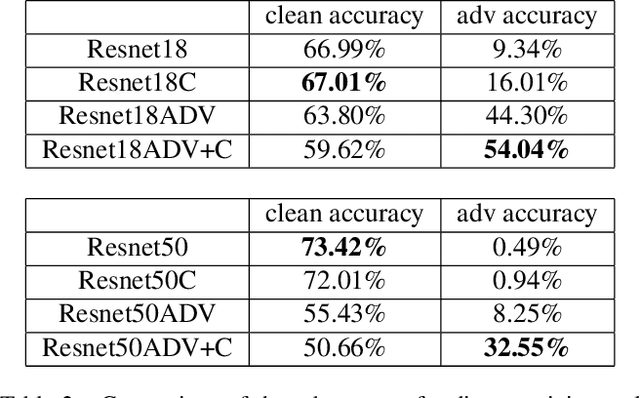
Deep learning models suffer from the problem of semantic discontinuity: small perturbations in the input space tend to cause semantic-level interference to the model output. We argue that the semantic discontinuity results from these inappropriate training targets and contributes to notorious issues such as adversarial robustness, interpretability, etc. We first conduct data analysis to provide evidence of semantic discontinuity in existing deep learning models, and then design a simple semantic continuity constraint which theoretically enables models to obtain smooth gradients and learn semantic-oriented features. Qualitative and quantitative experiments prove that semantically continuous models successfully reduce the use of non-semantic information, which further contributes to the improvement in adversarial robustness, interpretability, model transfer, and machine bias.