Quantifying the Prediction Uncertainty of Machine Learning Models for Individual Data

Machine learning models have exhibited exceptional results in various domains. The most prevalent approach for learning is the empirical risk minimizer (ERM), which adapts the model's weights to reduce the loss on a training set and subsequently leverages these weights to predict the label for new test data. Nonetheless, ERM makes the assumption that the test distribution is similar to the training distribution, which may not always hold in real-world situations. In contrast, the predictive normalized maximum likelihood (pNML) was proposed as a min-max solution for the individual setting where no assumptions are made on the distribution of the tested input. This study investigates pNML's learnability for linear regression and neural networks, and demonstrates that pNML can improve the performance and robustness of these models on various tasks. Moreover, the pNML provides an accurate confidence measure for its output, showcasing state-of-the-art results for out-of-distribution detection, resistance to adversarial attacks, and active learning.

Semi-supervised Adversarial Learning for Complementary Item Recommendation

Complementary item recommendations are a ubiquitous feature of modern e-commerce sites. Such recommendations are highly effective when they are based on collaborative signals like co-purchase statistics. In certain online marketplaces, however, e.g., on online auction sites, constantly new items are added to the catalog. In such cases, complementary item recommendations are often based on item side-information due to a lack of interaction data. In this work, we propose a novel approach that can leverage both item side-information and labeled complementary item pairs to generate effective complementary recommendations for cold items, i.e., for items for which no co-purchase statistics yet exist. Given that complementary items typically have to be of a different category than the seed item, we technically maintain a latent space for each item category. Simultaneously, we learn to project distributed item representations into these category spaces to determine suitable recommendations. The main learning process in our architecture utilizes labeled pairs of complementary items. In addition, we adopt ideas from Cycle Generative Adversarial Networks (CycleGAN) to leverage available item information even in case no labeled data exists for a given item and category. Experiments on three e-commerce datasets show that our method is highly effective.

Beyond Ridge Regression for Distribution-Free Data

In supervised batch learning, the predictive normalized maximum likelihood (pNML) has been proposed as the min-max regret solution for the distribution-free setting, where no distributional assumptions are made on the data. However, the pNML is not defined for a large capacity hypothesis class as over-parameterized linear regression. For a large class, a common approach is to use regularization or a model prior. In the context of online prediction where the min-max solution is the Normalized Maximum Likelihood (NML), it has been suggested to use NML with ``luckiness'': A prior-like function is applied to the hypothesis class, which reduces its effective size. Motivated by the luckiness concept, for linear regression we incorporate a luckiness function that penalizes the hypothesis proportionally to its l2 norm. This leads to the ridge regression solution. The associated pNML with luckiness (LpNML) prediction deviates from the ridge regression empirical risk minimizer (Ridge ERM): When the test data reside in the subspace corresponding to the small eigenvalues of the empirical correlation matrix of the training data, the prediction is shifted toward 0. Our LpNML reduces the Ridge ERM error by up to 20% for the PMLB sets, and is up to 4.9% more robust in the presence of distribution shift compared to recent leading methods for UCI sets.

Single Layer Predictive Normalized Maximum Likelihood for Out-of-Distribution Detection

Detecting out-of-distribution (OOD) samples is vital for developing machine learning based models for critical safety systems. Common approaches for OOD detection assume access to some OOD samples during training which may not be available in a real-life scenario. Instead, we utilize the {\em predictive normalized maximum likelihood} (pNML) learner, in which no assumptions are made on the tested input. We derive an explicit expression of the pNML and its generalization error, denoted as the {\em regret}, for a single layer neural network (NN). We show that this learner generalizes well when (i) the test vector resides in a subspace spanned by the eigenvectors associated with the large eigenvalues of the empirical correlation matrix of the training data, or (ii) the test sample is far from the decision boundary. Furthermore, we describe how to efficiently apply the derived pNML regret to any pretrained deep NN, by employing the explicit pNML for the last layer, followed by the softmax function. Applying the derived regret to deep NN requires neither additional tunable parameters nor extra data. We extensively evaluate our approach on 74 OOD detection benchmarks using DenseNet-100, ResNet-34, and WideResNet-40 models trained with CIFAR-100, CIFAR-10, SVHN, and ImageNet-30 showing a significant improvement of up to 15.6\% over recent leading methods.

Utilizing Adversarial Targeted Attacks to Boost Adversarial Robustness

Adversarial attacks have been shown to be highly effective at degrading the performance of deep neural networks (DNNs). The most prominent defense is adversarial training, a method for learning a robust model. Nevertheless, adversarial training does not make DNNs immune to adversarial perturbations. We propose a novel solution by adopting the recently suggested Predictive Normalized Maximum Likelihood. Specifically, our defense performs adversarial targeted attacks according to different hypotheses, where each hypothesis assumes a specific label for the test sample. Then, by comparing the hypothesis probabilities, we predict the label. Our refinement process corresponds to recent findings of the adversarial subspace properties. We extensively evaluate our approach on 16 adversarial attack benchmarks using ResNet-50, WideResNet-28, and a2-layer ConvNet trained with ImageNet, CIFAR10, and MNIST, showing a significant improvement of up to 5.7%, 3.7%, and 0.6% respectively.

The Predictive Normalized Maximum Likelihood for Over-parameterized Linear Regression with Norm Constraint: Regret and Double Descent

A fundamental tenet of learning theory is that a trade-off exists between the complexity of a prediction rule and its ability to generalize. The double-decent phenomenon shows that modern machine learning models do not obey this paradigm: beyond the interpolation limit, the test error declines as model complexity increases. We investigate over-parameterization in linear regression using the recently proposed predictive normalized maximum likelihood (pNML) learner which is the min-max regret solution for individual data. We derive an upper bound of its regret and show that if the test sample lies mostly in a subspace spanned by the eigenvectors associated with the large eigenvalues of the empirical correlation matrix of the training data, the model generalizes despite its over-parameterized nature. We demonstrate the use of the pNML regret as a point-wise learnability measure on synthetic data and that it can successfully predict the double-decent phenomenon using the UCI dataset.

Learning Rotation Invariant Features for Cryogenic Electron Microscopy Image Reconstruction

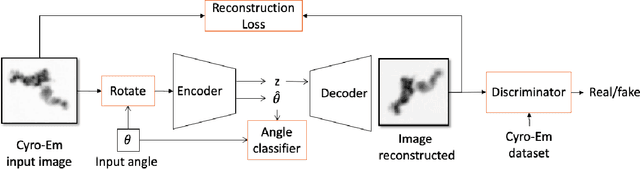
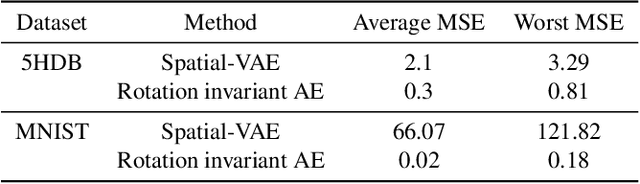
Cryo-Electron Microscopy (Cryo-EM) is a Nobel prize-winning technology for determining the 3D structure of particles at near-atomic resolution. A fundamental step in the recovering of the 3D single-particle structure is to align its 2D projections; thus, the construction of a canonical representation with a fixed rotation angle is required. Most approaches use discrete clustering which fails to capture the continuous nature of image rotation, others suffer from low-quality image reconstruction. We propose a novel method that leverages the recent development in the generative adversarial networks. We introduce an encoder-decoder with a rotation angle classifier. In addition, we utilize a discriminator on the decoder output to minimize the reconstruction error. We demonstrate our approach with the Cryo-EM 5HDB and the rotated MNIST datasets showing substantial improvement over recent methods.

Balancing Specialization, Generalization, and Compression for Detection and Tracking

We propose a method for specializing deep detectors and trackers to restricted settings. Our approach is designed with the following goals in mind: (a) Improving accuracy in restricted domains; (b) preventing overfitting to new domains and forgetting of generalized capabilities; (c) aggressive model compression and acceleration. To this end, we propose a novel loss that balances compression and acceleration of a deep learning model vs. loss of generalization capabilities. We apply our method to the existing tracker and detector models. We report detection results on the VIRAT and CAVIAR data sets. These results show our method to offer unprecedented compression rates along with improved detection. We apply our loss for tracker compression at test time, as it processes each video. Our tests on the OTB2015 benchmark show that applying compression during test time actually improves tracking performance.

A New Look at an Old Problem: A Universal Learning Approach to Linear Regression

Linear regression is a classical paradigm in statistics. A new look at it is provided via the lens of universal learning. In applying universal learning to linear regression the hypotheses class represents the label $y\in {\cal R}$ as a linear combination of the feature vector $x^T\theta$ where $x\in {\cal R}^M$, within a Gaussian error. The Predictive Normalized Maximum Likelihood (pNML) solution for universal learning of individual data can be expressed analytically in this case, as well as its associated learnability measure. Interestingly, the situation where the number of parameters $M$ may even be larger than the number of training samples $N$ can be examined. As expected, in this case learnability cannot be attained in every situation; nevertheless, if the test vector resides mostly in a subspace spanned by the eigenvectors associated with the large eigenvalues of the empirical correlation matrix of the training data, linear regression can generalize despite the fact that it uses an ``over-parametrized'' model. We demonstrate the results with a simulation of fitting a polynomial to data with a possibly large polynomial degree.

Deep pNML: Predictive Normalized Maximum Likelihood for Deep Neural Networks

The Predictive Normalized Maximum Likelihood (pNML) scheme has been recently suggested for universal learning in the individual setting, where both the training and test samples are individual data. The goal of universal learning is to compete with a ``genie'' or reference learner that knows the data values, but is restricted to use a learner from a given model class. The pNML minimizes the associated regret for any possible value of the unknown label. Furthermore, its min-max regret can serve as a pointwise measure of learnability for the specific training and data sample. In this work we examine the pNML and its associated learnability measure for the Deep Neural Network (DNN) model class. As shown, the pNML outperforms the commonly used Empirical Risk Minimization (ERM) approach and provides robustness against adversarial attacks. Together with its learnability measure it can detect out of distribution test examples, be tolerant to noisy labels and serve as a confidence measure for the ERM. Finally, we extend the pNML to a ``twice universal'' solution, that provides universality for model class selection and generates a learner competing with the best one from all model classes.