On the Trainability of Masked Diffusion Language Models via Blockwise Locality

Masked diffusion language models (MDMs) have recently emerged as a promising alternative to standard autoregressive large language models (AR-LLMs), yet their optimization can be substantially less stable. We study blockwise MDMs and compare them with AR-LLMs on three controlled tasks that stress different aspects of structured generation: in-context linear regression, graph path-finding, and Sudoku solving. We find that standard random-masking MDMs fail to reliably learn linear regression, exhibit high variance training dynamics on graph path-finding, while outperforming AR-LLMs on Sudoku. To mitigate these instabilities, we propose two locality aware blockwise models, namely Jigsaw and Scatter, that inject left-to-right inductive bias by enforcing autoregressive locality within blocks while preserving iterative refinement at the block level. Empirically, Jigsaw matches AR-LLM stability on linear regression and remains strong on Sudoku, while Scatter retains diffusion's planning advantage on path-finding. Our results indicate that standard random-masking MDMs, even with blockwise variants, may be a suboptimal instantiation of diffusion LMs for ordered generation, motivating models beyond random masking.

EE-MCP: Self-Evolving MCP-GUI Agents via Automated Environment Generation and Experience Learning

Computer-use agents that combine GUI interaction with structured API calls via the Model Context Protocol (MCP) show promise for automating software tasks. However, existing approaches lack a principled understanding of how agents should balance these two modalities and how to enable iterative self-improvement across diverse applications. We formulate MCP-GUI interplay as a unified hybrid policy learning problem where the agent learns when each modality provides complementary advantages, and show that distillation and experience augmentation target fundamentally different failure modes - requiring application-aware mechanism selection. Built on this formulation, we propose a self-evolving framework with a fully automatic pipeline that orchestrates automatic environment generation and validation, trajectory collection, gap-driven task synthesis, and quality-filtered training - all without manual intervention. A key innovation is our experience bank, which accumulates LLM-learned rules from trajectory comparison, enabling inference-time improvement without fine-tuning. Systematic \textbf{cross-application analysis} across three desktop applications reveals that the optimal strategy depends on MCP-GUI composition: distillation achieves 77.8\% pass rate on MCP-dominant tasks (+17.8pp), while the experience bank excels on GUI-intensive tasks (+10.0pp).

Impact of Connectivity on Laplacian Representations in Reinforcement Learning

Learning compact state representations in Markov Decision Processes (MDPs) has proven crucial for addressing the curse of dimensionality in large-scale reinforcement learning (RL) problems. Existing principled approaches leverage structural priors on the MDP by constructing state representations as linear combinations of the state-graph Laplacian eigenvectors. When the transition graph is unknown or the state space is prohibitively large, the graph spectral features can be estimated directly via sample trajectories. In this work, we prove an upper bound on the approximation error of linear value function approximation under the learned spectral features. We show how this error scales with the algebraic connectivity of the state-graph, grounding the approximation quality in the topological structure of the MDP. We further bound the error introduced by the eigenvector estimation itself, leading to an end-to-end error decomposition across the representation learning pipeline. Additionally, our expression of the Laplacian operator for the RL setting, although equivalent to existing ones, prevents some common misunderstandings, of which we show some examples from the literature. Our results hold for general (non-uniform) policies without any assumptions on the symmetry of the induced transition kernel. We validate our theoretical findings with numerical simulations on gridworld environments.

Logics-STEM: Empowering LLM Reasoning via Failure-Driven Post-Training and Document Knowledge Enhancement

We present Logics-STEM, a state-of-the-art reasoning model fine-tuned on Logics-STEM-SFT-Dataset, a high-quality and diverse dataset at 10M scale that represents one of the largest-scale open-source long chain-of-thought corpora. Logics-STEM targets reasoning tasks in the domains of Science, Technology, Engineering, and Mathematics (STEM), and exhibits exceptional performance on STEM-related benchmarks with an average improvement of 4.68% over the next-best model at 8B scale. We attribute the gains to our data-algorithm co-design engine, where they are jointly optimized to fit a gold-standard distribution behind reasoning. Data-wise, the Logics-STEM-SFT-Dataset is constructed from a meticulously designed data curation engine with 5 stages to ensure the quality, diversity, and scalability, including annotation, deduplication, decontamination, distillation, and stratified sampling. Algorithm-wise, our failure-driven post-training framework leverages targeted knowledge retrieval and data synthesis around model failure regions in the Supervised Fine-tuning (SFT) stage to effectively guide the second-stage SFT or the reinforcement learning (RL) for better fitting the target distribution. The superior empirical performance of Logics-STEM reveals the vast potential of combining large-scale open-source data with carefully designed synthetic data, underscoring the critical role of data-algorithm co-design in enhancing reasoning capabilities through post-training. We make both the Logics-STEM models (8B and 32B) and the Logics-STEM-SFT-Dataset (10M and downsampled 2.2M versions) publicly available to support future research in the open-source community.

Adaptive Multi-view Graph Contrastive Learning via Fractional-order Neural Diffusion Networks

Graph contrastive learning (GCL) learns node and graph representations by contrasting multiple views of the same graph. Existing methods typically rely on fixed, handcrafted views-usually a local and a global perspective, which limits their ability to capture multi-scale structural patterns. We present an augmentation-free, multi-view GCL framework grounded in fractional-order continuous dynamics. By varying the fractional derivative order $α\in (0,1]$, our encoders produce a continuous spectrum of views: small $α$ yields localized features, while large $α$ induces broader, global aggregation. We treat $α$ as a learnable parameter so the model can adapt diffusion scales to the data and automatically discover informative views. This principled approach generates diverse, complementary representations without manual augmentations. Extensive experiments on standard benchmarks demonstrate that our method produces more robust and expressive embeddings and outperforms state-of-the-art GCL baselines.

On the Importance of Task Complexity in Evaluating LLM-Based Multi-Agent Systems

Large language model multi-agent systems (LLM-MAS) offer a promising paradigm for harnessing collective intelligence to achieve more advanced forms of AI behaviour. While recent studies suggest that LLM-MAS can outperform LLM single-agent systems (LLM-SAS) on certain tasks, the lack of systematic experimental designs limits the strength and generality of these conclusions. We argue that a principled understanding of task complexity, such as the degree of sequential reasoning required and the breadth of capabilities involved, is essential for assessing the effectiveness of LLM-MAS in task solving. To this end, we propose a theoretical framework characterising tasks along two dimensions: depth, representing reasoning length, and width, representing capability diversity. We theoretically examine a representative class of LLM-MAS, namely the multi-agent debate system, and empirically evaluate its performance in both discriminative and generative tasks with varying depth and width. Theoretical and empirical results show that the benefit of LLM-MAS over LLM-SAS increases with both task depth and width, and the effect is more pronounced with respect to depth. This clarifies when LLM-MAS are beneficial and provides a principled foundation for designing future LLM-MAS methods and benchmarks.

A Stage-Aware Mixture of Experts Framework for Neurodegenerative Disease Progression Modelling

The long-term progression of neurodegenerative diseases is commonly conceptualized as a spatiotemporal diffusion process that consists of a graph diffusion process across the structural brain connectome and a localized reaction process within brain regions. However, modeling this progression remains challenging due to 1) the scarcity of longitudinal data obtained through irregular and infrequent subject visits and 2) the complex interplay of pathological mechanisms across brain regions and disease stages, where traditional models assume fixed mechanisms throughout disease progression. To address these limitations, we propose a novel stage-aware Mixture of Experts (MoE) framework that explicitly models how different contributing mechanisms dominate at different disease stages through time-dependent expert weighting.Data-wise, we utilize an iterative dual optimization method to properly estimate the temporal position of individual observations, constructing a co hort-level progression trajectory from irregular snapshots. Model-wise, we enhance the spatial component with an inhomogeneous graph neural diffusion model (IGND) that allows diffusivity to vary based on node states and time, providing more flexible representations of brain networks. We also introduce a localized neural reaction module to capture complex dynamics beyond standard processes.The resulting IGND-MoE model dynamically integrates these components across temporal states, offering a principled way to understand how stage-specific pathological mechanisms contribute to progression. The stage-wise weights yield novel clinical insights that align with literature, suggesting that graph-related processes are more influential at early stages, while other unknown physical processes become dominant later on.

Heterogeneous Graph Structure Learning through the Lens of Data-generating Processes

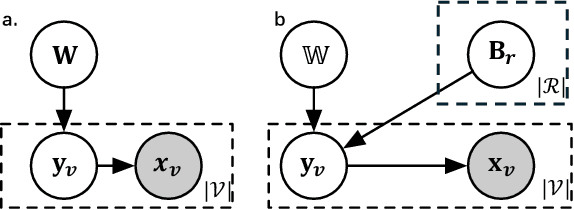
Inferring the graph structure from observed data is a key task in graph machine learning to capture the intrinsic relationship between data entities. While significant advancements have been made in learning the structure of homogeneous graphs, many real-world graphs exhibit heterogeneous patterns where nodes and edges have multiple types. This paper fills this gap by introducing the first approach for heterogeneous graph structure learning (HGSL). To this end, we first propose a novel statistical model for the data-generating process (DGP) of heterogeneous graph data, namely hidden Markov networks for heterogeneous graphs (H2MN). Then we formalize HGSL as a maximum a-posterior estimation problem parameterized by such DGP and derive an alternating optimization method to obtain a solution together with a theoretical justification of the optimization conditions. Finally, we conduct extensive experiments on both synthetic and real-world datasets to demonstrate that our proposed method excels in learning structure on heterogeneous graphs in terms of edge type identification and edge weight recovery.

Effects of Random Edge-Dropping on Over-Squashing in Graph Neural Networks

Message Passing Neural Networks (MPNNs) are a class of Graph Neural Networks (GNNs) that leverage the graph topology to propagate messages across increasingly larger neighborhoods. The message-passing scheme leads to two distinct challenges: over-smoothing and over-squashing. While several algorithms, e.g. DropEdge and its variants -- DropNode, DropAgg and DropGNN -- have successfully addressed the over-smoothing problem, their impact on over-squashing remains largely unexplored. This represents a critical gap in the literature as failure to mitigate over-squashing would make these methods unsuitable for long-range tasks. In this work, we take the first step towards closing this gap by studying the aforementioned algorithms in the context of over-squashing. We present novel theoretical results that characterize the negative effects of DropEdge on sensitivity between distant nodes, suggesting its unsuitability for long-range tasks. Our findings are easily extended to its variants, allowing us to build a comprehensive understanding of how they affect over-squashing. We evaluate these methods using real-world datasets, demonstrating their detrimental effects. Specifically, we show that while DropEdge-variants improve test-time performance in short range tasks, they deteriorate performance in long-range ones. Our theory explains these results as follows: random edge-dropping lowers the effective receptive field of GNNs, which although beneficial for short-range tasks, misaligns the models on long-range ones. This forces the models to overfit to short-range artefacts in the training set, resulting in poor generalization. Our conclusions highlight the need to re-evaluate various methods designed for training deep GNNs, with a renewed focus on modelling long-range interactions.

Hypergraph Node Classification With Graph Neural Networks

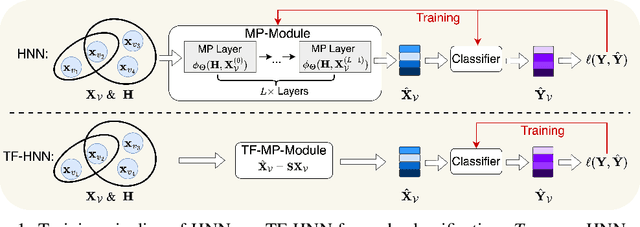
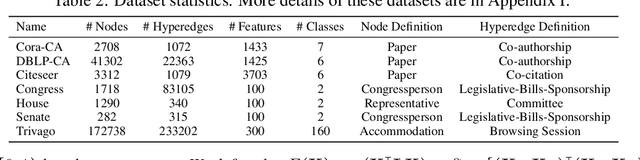
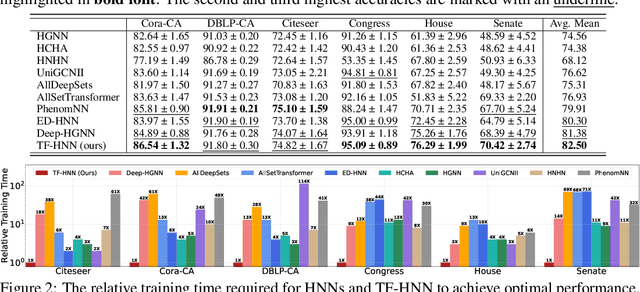
Hypergraphs, with hyperedges connecting more than two nodes, are key for modelling higher-order interactions in real-world data. The success of graph neural networks (GNNs) reveals the capability of neural networks to process data with pairwise interactions. This inspires the usage of neural networks for data with higher-order interactions, thereby leading to the development of hypergraph neural networks (HyperGNNs). GNNs and HyperGNNs are typically considered distinct since they are designed for data on different geometric topologies. However, in this paper, we theoretically demonstrate that, in the context of node classification, most HyperGNNs can be approximated using a GNN with a weighted clique expansion of the hypergraph. This leads to WCE-GNN, a simple and efficient framework comprising a GNN and a weighted clique expansion (WCE), for hypergraph node classification. Experiments on nine real-world hypergraph node classification benchmarks showcase that WCE-GNN demonstrates not only higher classification accuracy compared to state-of-the-art HyperGNNs, but also superior memory and runtime efficiency.