SPRINT: Semi-supervised Prototypical Representation for Few-Shot Class-Incremental Tabular Learning

Real-world systems must continuously adapt to novel concepts from limited data without forgetting previously acquired knowledge. While Few-Shot Class-Incremental Learning (FSCIL) is established in computer vision, its application to tabular domains remains largely unexplored. Unlike images, tabular streams (e.g., logs, sensors) offer abundant unlabeled data, a scarcity of expert annotations and negligible storage costs, features ignored by existing vision-based methods that rely on restrictive buffers. We introduce SPRINT, the first FSCIL framework tailored for tabular distributions. SPRINT introduces a mixed episodic training strategy that leverages confidence-based pseudo-labeling to enrich novel class representations and exploits low storage costs to retain base class history. Extensive evaluation across six diverse benchmarks spanning cybersecurity, healthcare, and ecological domains, demonstrates SPRINT's cross-domain robustness. It achieves a state-of-the-art average accuracy of 77.37% (5-shot), outperforming the strongest incremental baseline by 4.45%.

Online Learning for Multi-Layer Hierarchical Inference under Partial and Policy-Dependent Feedback

Hierarchical inference systems route tasks across multiple computational layers, where each node may either finalize a prediction locally or offload the task to a node in the next layer for further processing. Learning optimal routing policies in such systems is challenging: inference loss is defined recursively across layers, while feedback on prediction error is revealed only at a terminal oracle layer. This induces a partial, policy-dependent feedback structure in which observability probabilities decay with depth, causing importance-weighted estimators to suffer from amplified variance. We study online routing for multi-layer hierarchical inference under long-term resource constraints and terminal-only feedback. We formalize the recursive loss structure and show that naive importance-weighted contextual bandit methods become unstable as feedback probability decays along the hierarchy. To address this, we develop a variance-reduced EXP4-based algorithm integrated with Lyapunov optimization, yielding unbiased loss estimation and stable learning under sparse and policy-dependent feedback. We provide regret guarantees relative to the best fixed routing policy in hindsight and establish near-optimality under stochastic arrivals and resource constraints. Experiments on large-scale multi-task workloads demonstrate improved stability and performance compared to standard importance-weighted approaches.

Optimal Resource Allocation for ML Model Training and Deployment under Concept Drift

We study how to allocate resources for training and deployment of machine learning (ML) models under concept drift and limited budgets. We consider a setting in which a model provider distributes trained models to multiple clients whose devices support local inference but lack the ability to retrain those models, placing the burden of performance maintenance on the provider. We introduce a model-agnostic framework that captures the interaction between resource allocation, concept drift dynamics, and deployment timing. We show that optimal training policies depend critically on the aging properties of concept durations. Under sudden concept changes, we derive optimal training policies subject to budget constraints when concept durations follow distributions with Decreasing Mean Residual Life (DMRL), and show that intuitive heuristics are provably suboptimal under Increasing Mean Residual Life (IMRL). We further study model deployment under communication constraints, prove that the associated optimization problem is quasi-convex under mild conditions, and propose a randomized scheduling strategy that achieves near-optimal client-side performance. These results offer theoretical and algorithmic foundations for cost-efficient ML model management under concept drift, with implications for continual learning, distributed inference, and adaptive ML systems.

Connecting the Dots: Detecting Adversarial Perturbations Using Context Inconsistency

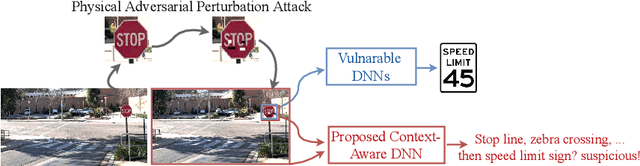
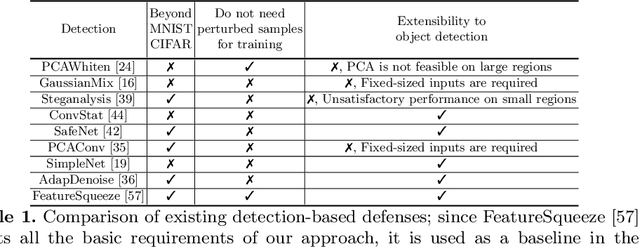
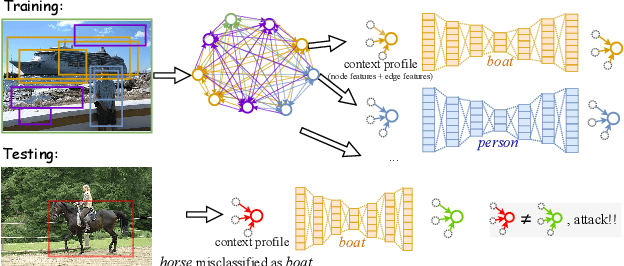
There has been a recent surge in research on adversarial perturbations that defeat Deep Neural Networks (DNNs) in machine vision; most of these perturbation-based attacks target object classifiers. Inspired by the observation that humans are able to recognize objects that appear out of place in a scene or along with other unlikely objects, we augment the DNN with a system that learns context consistency rules during training and checks for the violations of the same during testing. Our approach builds a set of auto-encoders, one for each object class, appropriately trained so as to output a discrepancy between the input and output if an added adversarial perturbation violates context consistency rules. Experiments on PASCAL VOC and MS COCO show that our method effectively detects various adversarial attacks and achieves high ROC-AUC (over 0.95 in most cases); this corresponds to over 20% improvement over a state-of-the-art context-agnostic method.

Geometric Laplacian Eigenmap Embedding

Graph embedding seeks to build a low-dimensional representation of a graph G. This low-dimensional representation is then used for various downstream tasks. One popular approach is Laplacian Eigenmaps, which constructs a graph embedding based on the spectral properties of the Laplacian matrix of G. The intuition behind it, and many other embedding techniques, is that the embedding of a graph must respect node similarity: similar nodes must have embeddings that are close to one another. Here, we dispose of this distance-minimization assumption. Instead, we use the Laplacian matrix to find an embedding with geometric properties instead of spectral ones, by leveraging the so-called simplex geometry of G. We introduce a new approach, Geometric Laplacian Eigenmap Embedding (or GLEE for short), and demonstrate that it outperforms various other techniques (including Laplacian Eigenmaps) in the tasks of graph reconstruction and link prediction.

Robust Coreset Construction for Distributed Machine Learning

Motivated by the need of solving machine learning problems over distributed datasets, we explore the use of coreset to reduce the communication overhead. Coreset is a summary of the original dataset in the form of a small weighted set in the same sample space. Compared to other data summaries, coreset has the advantage that it can be used as a proxy of the original dataset, potentially for different applications. However, existing coreset construction algorithms are each tailor-made for a specific machine learning problem. Thus, to solve different machine learning problems, one has to collect coresets of different types, defeating the purpose of saving communication overhead. We resolve this dilemma by developing coreset construction algorithms based on k-means/median clustering, that give a provably good approximation for a broad range of machine learning problems with sufficiently continuous cost functions. Through evaluations on diverse datasets and machine learning problems, we verify the robust performance of the proposed algorithms.