Higher-order methods for convex-concave min-max optimization and monotone variational inequalities

We provide improved convergence rates for constrained convex-concave min-max problems and monotone variational inequalities with higher-order smoothness. In min-max settings where the $p^{th}$-order derivatives are Lipschitz continuous, we give an algorithm HigherOrderMirrorProx that achieves an iteration complexity of $O(1/T^{\frac{p+1}{2}})$ when given access to an oracle for finding a fixed point of a $p^{th}$-order equation. We give analogous rates for the weak monotone variational inequality problem. For $p>2$, our results improve upon the iteration complexity of the first-order Mirror Prox method of Nemirovski [2004] and the second-order method of Monteiro and Svaiter [2012]. We further instantiate our entire algorithm in the unconstrained $p=2$ case.

Last-iterate convergence rates for min-max optimization

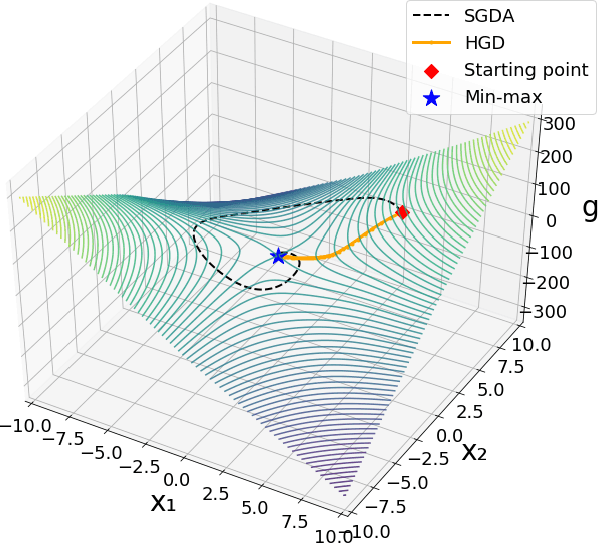
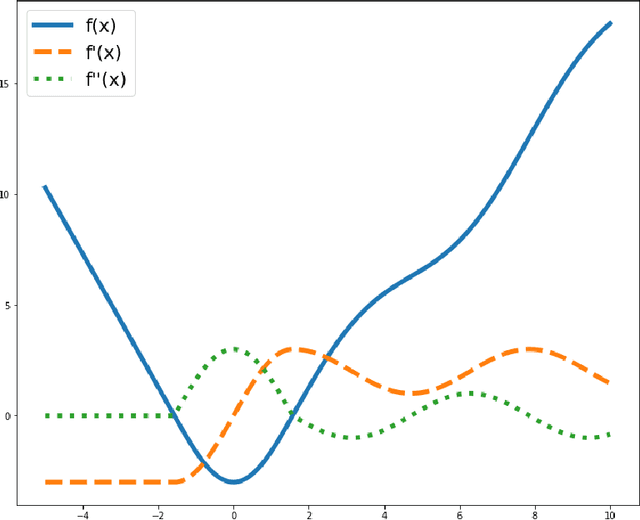
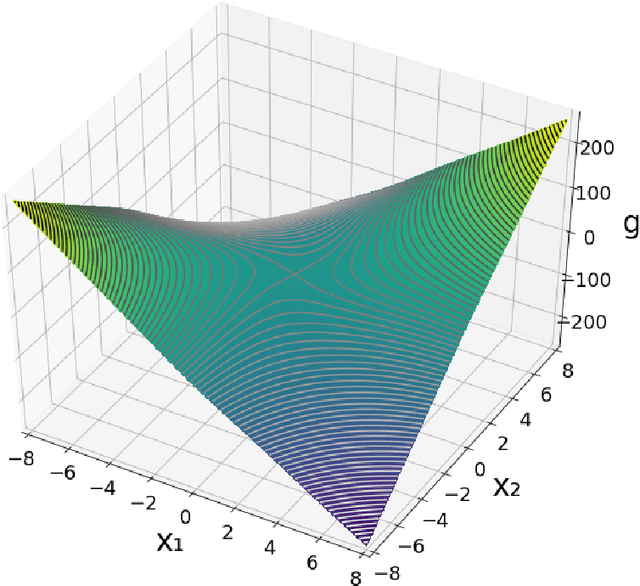
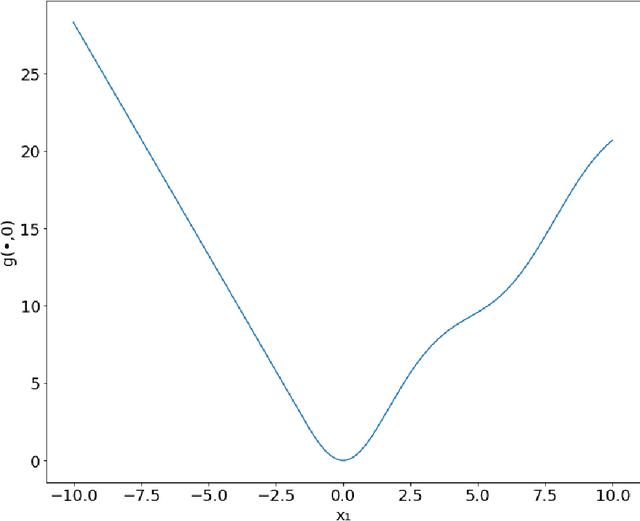
We study the problem of finding min-max solutions for smooth two-input objective functions. While classic results show average-iterate convergence rates for various algorithms, nonconvex applications such as training Generative Adversarial Networks require \emph{last-iterate} convergence guarantees, which are more difficult to prove. It has been an open problem as to whether any algorithm achieves non-asymptotic last-iterate convergence in settings beyond the bilinear and convex-strongly concave settings. In this paper, we study the Hamiltonian Gradient Descent (HGD) algorithm, and we show that HGD exhibits a \emph{linear} convergence rate in a variety of more general settings, including convex-concave settings that are "sufficiently bilinear." We also prove similar convergence rates for the Consensus Optimization (CO) algorithm of [MNG17] for some parameter settings of CO.

Faster Rates for Convex-Concave Games

We consider the use of no-regret algorithms to compute equilibria for particular classes of convex-concave games. While standard regret bounds would lead to convergence rates on the order of $O(T^{-1/2})$, recent work \citep{RS13,SALS15} has established $O(1/T)$ rates by taking advantage of a particular class of optimistic prediction algorithms. In this work we go further, showing that for a particular class of games one achieves a $O(1/T^2)$ rate, and we show how this applies to the Frank-Wolfe method and recovers a similar bound \citep{D15}. We also show that such no-regret techniques can even achieve a linear rate, $O(\exp(-T))$, for equilibrium computation under additional curvature assumptions.

Agnostic Estimation of Mean and Covariance

We consider the problem of estimating the mean and covariance of a distribution from iid samples in $\mathbb{R}^n$, in the presence of an $\eta$ fraction of malicious noise; this is in contrast to much recent work where the noise itself is assumed to be from a distribution of known type. The agnostic problem includes many interesting special cases, e.g., learning the parameters of a single Gaussian (or finding the best-fit Gaussian) when $\eta$ fraction of data is adversarially corrupted, agnostically learning a mixture of Gaussians, agnostic ICA, etc. We present polynomial-time algorithms to estimate the mean and covariance with error guarantees in terms of information-theoretic lower bounds. As a corollary, we also obtain an agnostic algorithm for Singular Value Decomposition.

Label optimal regret bounds for online local learning

We resolve an open question from (Christiano, 2014b) posed in COLT'14 regarding the optimal dependency of the regret achievable for online local learning on the size of the label set. In this framework the algorithm is shown a pair of items at each step, chosen from a set of $n$ items. The learner then predicts a label for each item, from a label set of size $L$ and receives a real valued payoff. This is a natural framework which captures many interesting scenarios such as collaborative filtering, online gambling, and online max cut among others. (Christiano, 2014a) designed an efficient online learning algorithm for this problem achieving a regret of $O(\sqrt{nL^3T})$, where $T$ is the number of rounds. Information theoretically, one can achieve a regret of $O(\sqrt{n \log L T})$. One of the main open questions left in this framework concerns closing the above gap. In this work, we provide a complete answer to the question above via two main results. We show, via a tighter analysis, that the semi-definite programming based algorithm of (Christiano, 2014a), in fact achieves a regret of $O(\sqrt{nLT})$. Second, we show a matching computational lower bound. Namely, we show that a polynomial time algorithm for online local learning with lower regret would imply a polynomial time algorithm for the planted clique problem which is widely believed to be hard. We prove a similar hardness result under a related conjecture concerning planted dense subgraphs that we put forth. Unlike planted clique, the planted dense subgraph problem does not have any known quasi-polynomial time algorithms. Computational lower bounds for online learning are relatively rare, and we hope that the ideas developed in this work will lead to lower bounds for other online learning scenarios as well.