Last-iterate convergence rates for min-max optimization
Paper and Code
Jun 05, 2019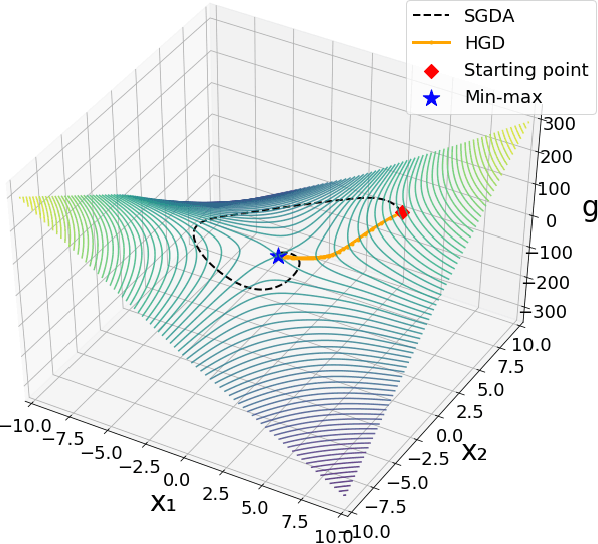
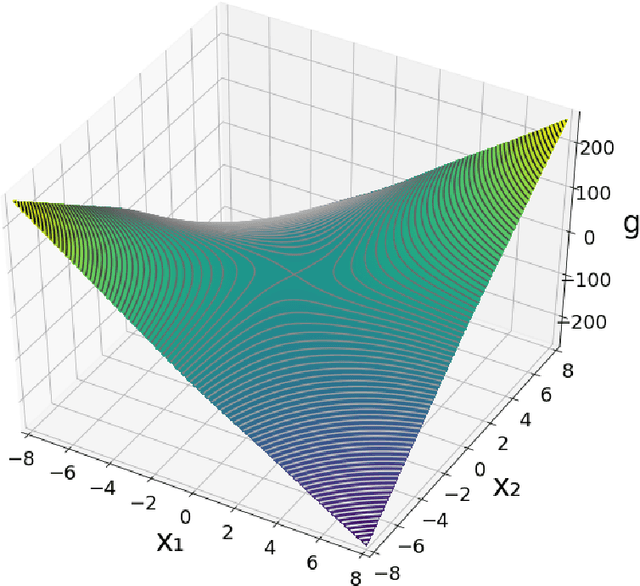
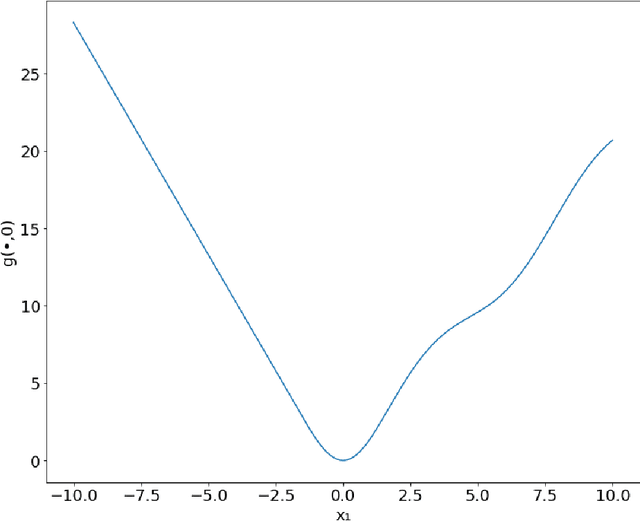
We study the problem of finding min-max solutions for smooth two-input objective functions. While classic results show average-iterate convergence rates for various algorithms, nonconvex applications such as training Generative Adversarial Networks require \emph{last-iterate} convergence guarantees, which are more difficult to prove. It has been an open problem as to whether any algorithm achieves non-asymptotic last-iterate convergence in settings beyond the bilinear and convex-strongly concave settings. In this paper, we study the Hamiltonian Gradient Descent (HGD) algorithm, and we show that HGD exhibits a \emph{linear} convergence rate in a variety of more general settings, including convex-concave settings that are "sufficiently bilinear." We also prove similar convergence rates for the Consensus Optimization (CO) algorithm of [MNG17] for some parameter settings of CO.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge