LLM-SR: Scientific Equation Discovery via Programming with Large Language Models

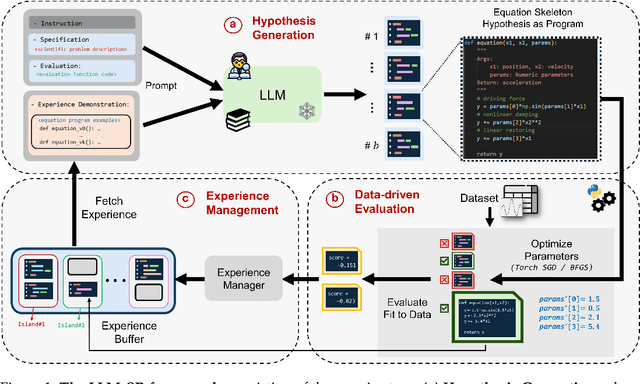
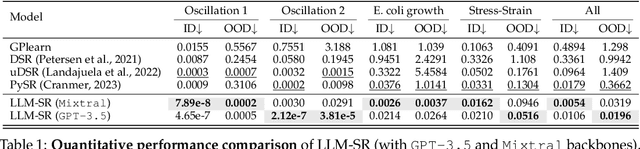
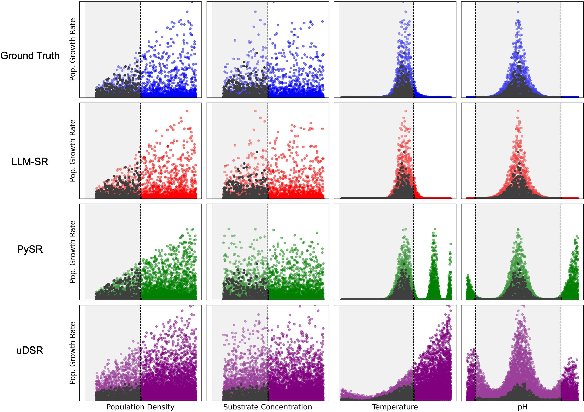
Mathematical equations have been unreasonably effective in describing complex natural phenomena across various scientific disciplines. However, discovering such insightful equations from data presents significant challenges due to the necessity of navigating extremely high-dimensional combinatorial and nonlinear hypothesis spaces. Traditional methods of equation discovery largely focus on extracting equations from data alone, often neglecting the rich domain-specific prior knowledge that scientists typically depend on. To bridge this gap, we introduce LLM-SR, a novel approach that leverages the extensive scientific knowledge and robust code generation capabilities of Large Language Models (LLMs) to discover scientific equations from data in an efficient manner. Specifically, LLM-SR treats equations as programs with mathematical operators and combines LLMs' scientific priors with evolutionary search over equation programs. The LLM iteratively proposes new equation skeletons, drawing from its physical understanding, which are then optimized against data to estimate skeleton parameters. We demonstrate LLM-SR's effectiveness across three diverse scientific domains, where it discovers physically accurate equations that provide significantly better fits to in-domain and out-of-domain data compared to the well-established equation discovery baselines

SNIP: Bridging Mathematical Symbolic and Numeric Realms with Unified Pre-training

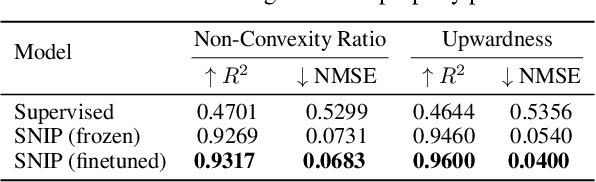
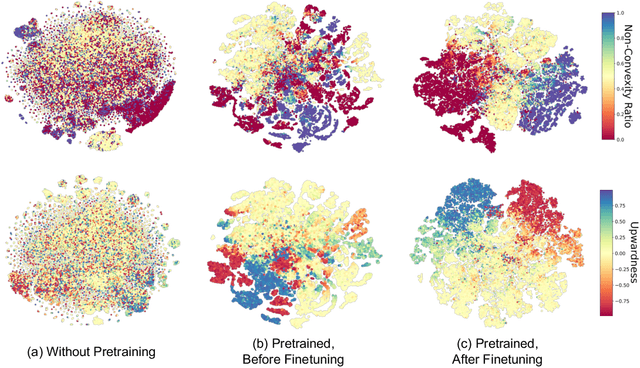
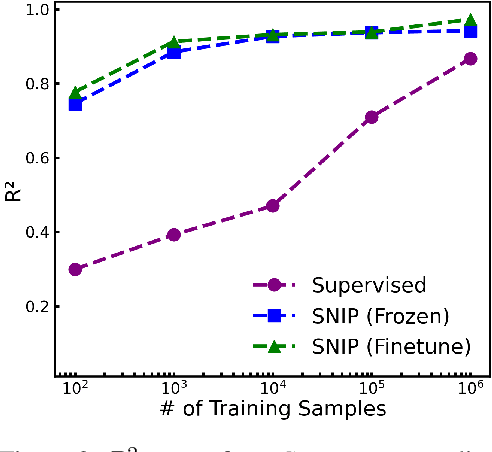
In an era where symbolic mathematical equations are indispensable for modeling complex natural phenomena, scientific inquiry often involves collecting observations and translating them into mathematical expressions. Recently, deep learning has emerged as a powerful tool for extracting insights from data. However, existing models typically specialize in either numeric or symbolic domains, and are usually trained in a supervised manner tailored to specific tasks. This approach neglects the substantial benefits that could arise from a task-agnostic unified understanding between symbolic equations and their numeric counterparts. To bridge the gap, we introduce SNIP, a Symbolic-Numeric Integrated Pre-training, which employs joint contrastive learning between symbolic and numeric domains, enhancing their mutual similarities in the pre-trained embeddings. By performing latent space analysis, we observe that SNIP provides cross-domain insights into the representations, revealing that symbolic supervision enhances the embeddings of numeric data and vice versa. We evaluate SNIP across diverse tasks, including symbolic-to-numeric mathematical property prediction and numeric-to-symbolic equation discovery, commonly known as symbolic regression. Results show that SNIP effectively transfers to various tasks, consistently outperforming fully supervised baselines and competing strongly with established task-specific methods, especially in few-shot learning scenarios where available data is limited.

Transformer-based Planning for Symbolic Regression

Symbolic regression (SR) is a challenging task in machine learning that involves finding a mathematical expression for a function based on its values. Recent advancements in SR have demonstrated the efficacy of pretrained transformer-based models for generating equations as sequences, which benefit from large-scale pretraining on synthetic datasets and offer considerable advantages over GP-based methods in terms of inference time. However, these models focus on supervised pretraining goals borrowed from text generation and ignore equation-specific objectives like accuracy and complexity. To address this, we propose TPSR, a Transformer-based Planning strategy for Symbolic Regression that incorporates Monte Carlo Tree Search into the transformer decoding process. TPSR, as opposed to conventional decoding strategies, allows for the integration of non-differentiable feedback, such as fitting accuracy and complexity, as external sources of knowledge into the equation generation process. Extensive experiments on various datasets show that our approach outperforms state-of-the-art methods, enhancing the model's fitting-complexity trade-off, extrapolation abilities, and robustness to noise. We also demonstrate that the utilization of various caching mechanisms can further enhance the efficiency of TPSR.

Transformer for Partial Differential Equations' Operator Learning

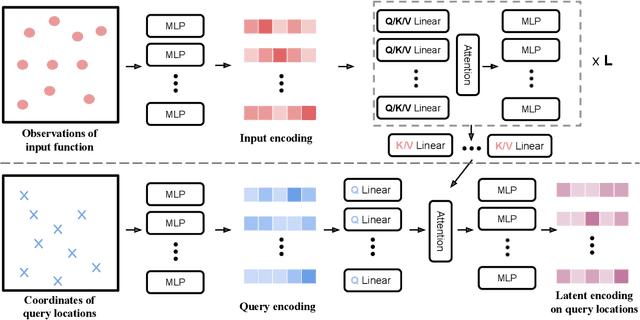
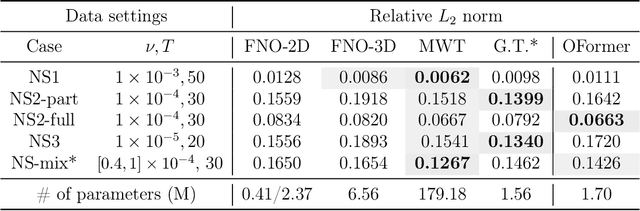
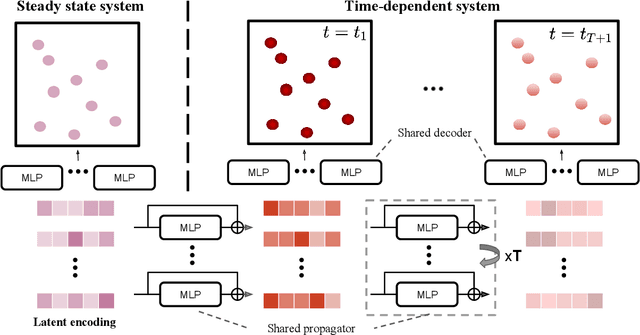
Data-driven learning of partial differential equations' solution operators has recently emerged as a promising paradigm for approximating the underlying solutions. The solution operators are usually parameterized by deep learning models that are built upon problem-specific inductive biases. An example is a convolutional or a graph neural network that exploits the local grid structure where functions' values are sampled. The attention mechanism, on the other hand, provides a flexible way to implicitly exploit the patterns within inputs, and furthermore, relationship between arbitrary query locations and inputs. In this work, we present an attention-based framework for data-driven operator learning, which we term Operator Transformer (OFormer). Our framework is built upon self-attention, cross-attention, and a set of point-wise multilayer perceptrons (MLPs), and thus it makes few assumptions on the sampling pattern of the input function or query locations. We show that the proposed framework is competitive on standard benchmark problems and can flexibly be adapted to randomly sampled input.

MeltpoolNet: Melt pool Characteristic Prediction in Metal Additive Manufacturing Using Machine Learning

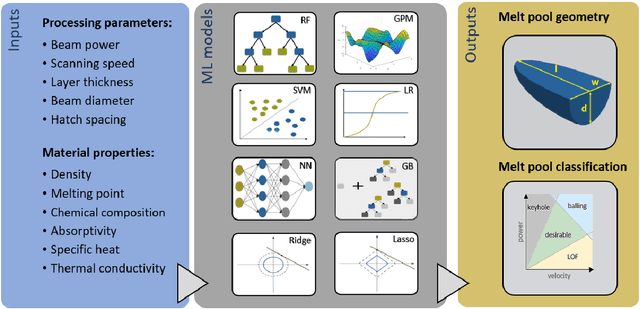
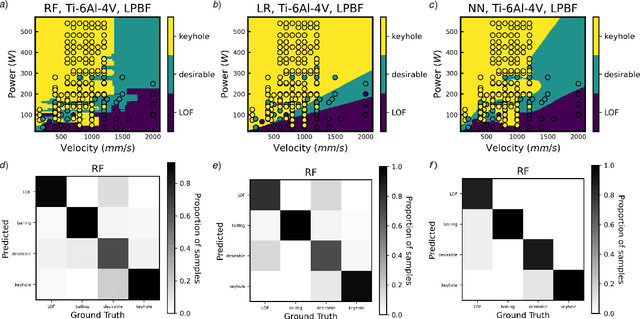
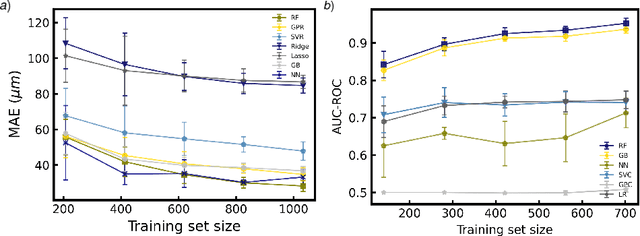
Characterizing meltpool shape and geometry is essential in metal Additive Manufacturing (MAM) to control the printing process and avoid defects. Predicting meltpool flaws based on process parameters and powder material is difficult due to the complex nature of MAM process. Machine learning (ML) techniques can be useful in connecting process parameters to the type of flaws in the meltpool. In this work, we introduced a comprehensive framework for benchmarking ML for melt pool characterization. An extensive experimental dataset has been collected from more than 80 MAM articles containing MAM processing conditions, materials, meltpool dimensions, meltpool modes and flaw types. We introduced physics-aware MAM featurization, versatile ML models, and evaluation metrics to create a comprehensive learning framework for meltpool defect and geometry prediction. This benchmark can serve as a basis for melt pool control and process optimization. In addition, data-driven explicit models have been identified to estimate meltpool geometry from process parameters and material properties which outperform Rosenthal estimation for meltpool geometry while maintaining interpretability.

Graph Neural Networks Accelerated Molecular Dynamics

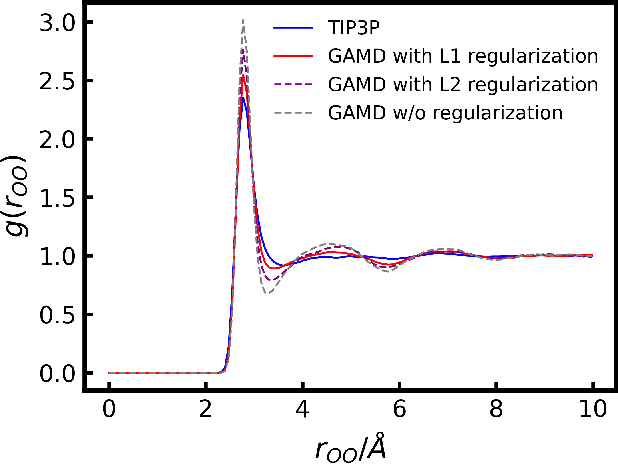
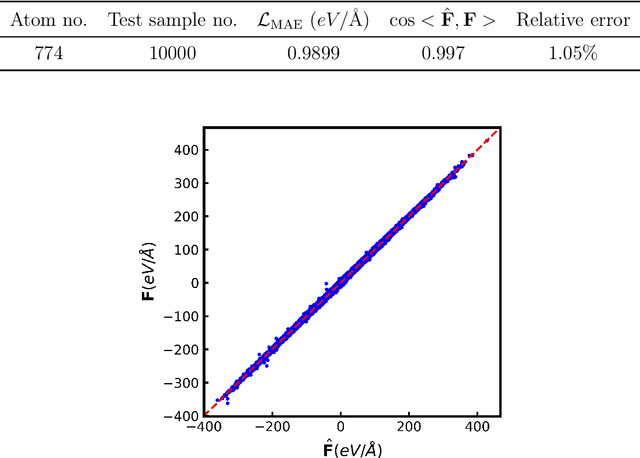
Molecular Dynamics (MD) simulation is a powerful tool for understanding the dynamics and structure of matter. Since the resolution of MD is atomic-scale, achieving long time-scale simulations with femtosecond integration is very expensive. In each MD step, numerous redundant computations are performed which can be learnt and avoided. These redundant computations can be surrogated and modeled by a deep learning model like a Graph Neural Network (GNN). In this work, we developed a GNN Accelerated Molecular Dynamics (GAMD) model that achieves fast and accurate force predictions and generates trajectories consistent with the classical MD simulations. Our results show that GAMD can accurately predict the dynamics of two typical molecular systems, Lennard-Jones (LJ) particles and Water (LJ+Electrostatics). GAMD's learning and inference are agnostic to the scale, where it can scale to much larger systems at test time. We also performed a comprehensive benchmark test comparing our implementation of GAMD to production-level MD softwares, where we showed GAMD is competitive with them on the large-scale simulation.

Graph Convolutional Neural Networks for Body Force Prediction

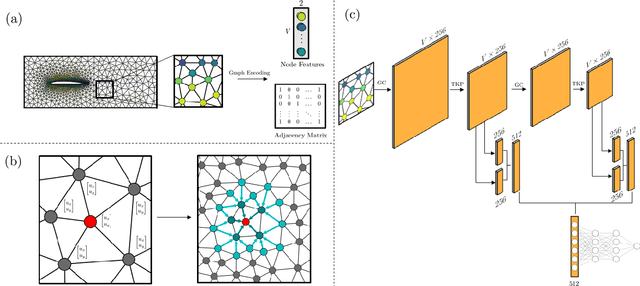
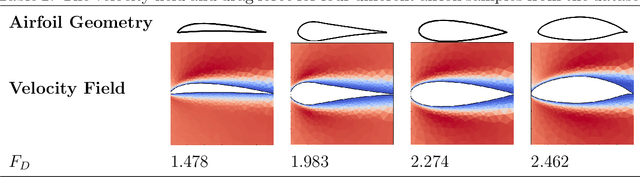
Many scientific and engineering processes produce spatially unstructured data. However, most data-driven models require a feature matrix that enforces both a set number and order of features for each sample. They thus cannot be easily constructed for an unstructured dataset. Therefore, a graph based data-driven model to perform inference on fields defined on an unstructured mesh, using a Graph Convolutional Neural Network (GCNN) is presented. The ability of the method to predict global properties from spatially irregular measurements with high accuracy is demonstrated by predicting the drag force associated with laminar flow around airfoils from scattered velocity measurements. The network can infer from field samples at different resolutions, and is invariant to the order in which the measurements within each sample are presented. The GCNN method, using inductive convolutional layers and adaptive pooling, is able to predict this quantity with a validation $R^{2}$ above 0.98, and a Normalized Mean Squared Error below 0.01, without relying on spatial structure.

Data-driven Identification of 2D Partial Differential Equations using extracted physical features

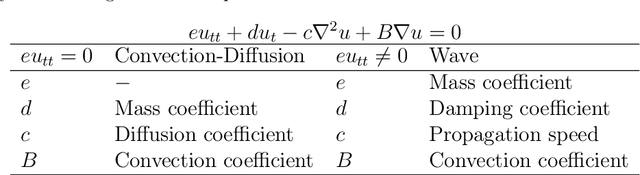
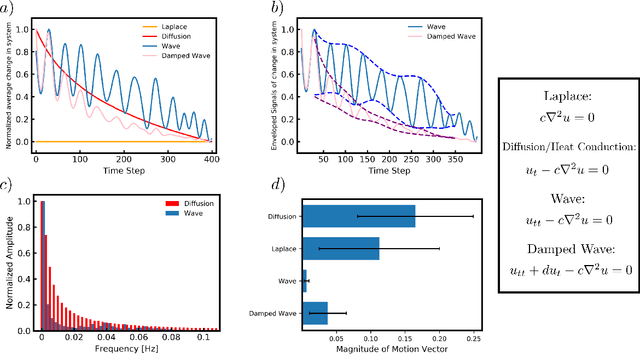
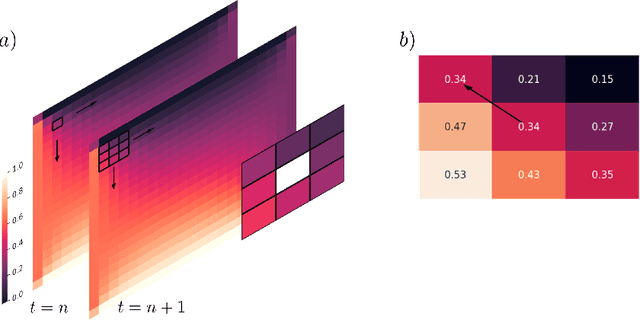
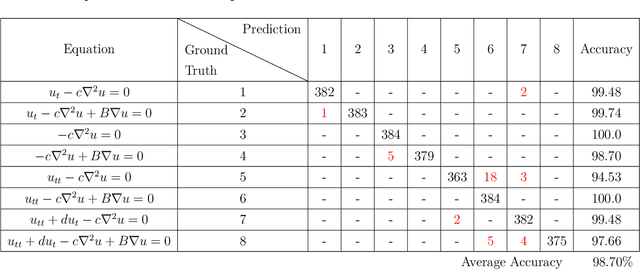
Many scientific phenomena are modeled by Partial Differential Equations (PDEs). The development of data gathering tools along with the advances in machine learning (ML) techniques have raised opportunities for data-driven identification of governing equations from experimentally observed data. We propose an ML method to discover the terms involved in the equation from two-dimensional spatiotemporal data. Robust and useful physical features are extracted from data samples to represent the specific behaviors imposed by each mathematical term in the equation. Compared to the previous models, this idea provides us with the ability to discover 2D equations with time derivatives of different orders, and also to identify new underlying physics on which the model has not been trained. Moreover, the model can work with small sets of low-resolution data while avoiding numerical differentiations. The results indicate robustness of the features extracted based on prior knowledge in comparison to automatically detected features by a Three-dimensional Convolutional Neural Network (3D CNN) given the same amounts of data. Although particular PDEs are studied in this work, the idea of the proposed approach could be extended for reliable identification of various PDEs.