Towards Scientific Discovery with Generative AI: Progress, Opportunities, and Challenges

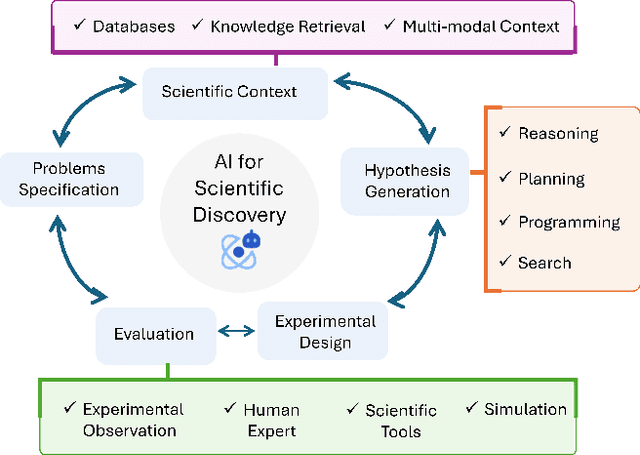
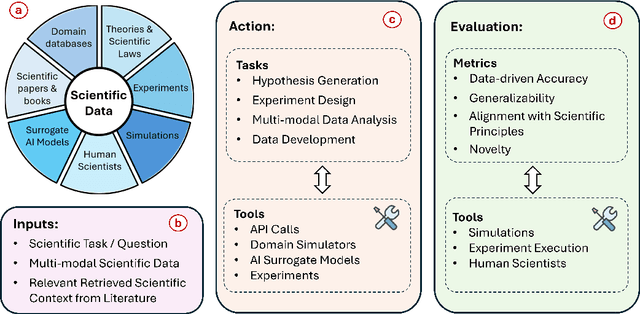
Scientific discovery is a complex cognitive process that has driven human knowledge and technological progress for centuries. While artificial intelligence (AI) has made significant advances in automating aspects of scientific reasoning, simulation, and experimentation, we still lack integrated AI systems capable of performing autonomous long-term scientific research and discovery. This paper examines the current state of AI for scientific discovery, highlighting recent progress in large language models and other AI techniques applied to scientific tasks. We then outline key challenges and promising research directions toward developing more comprehensive AI systems for scientific discovery, including the need for science-focused AI agents, improved benchmarks and evaluation metrics, multimodal scientific representations, and unified frameworks combining reasoning, theorem proving, and data-driven modeling. Addressing these challenges could lead to transformative AI tools to accelerate progress across disciplines towards scientific discovery.

LLM-SR: Scientific Equation Discovery via Programming with Large Language Models

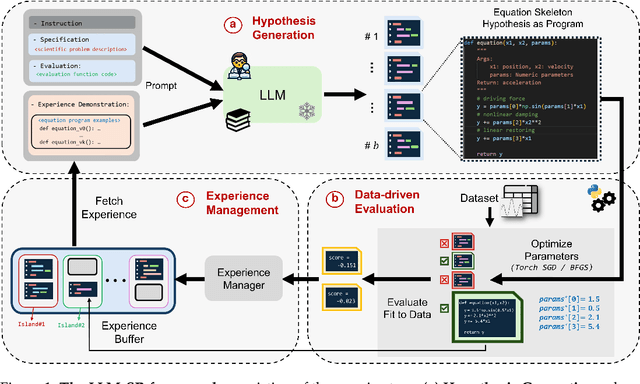
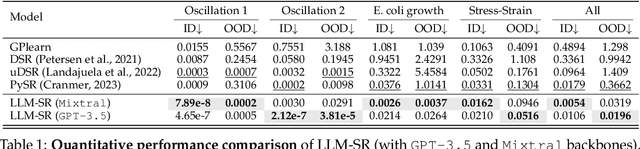
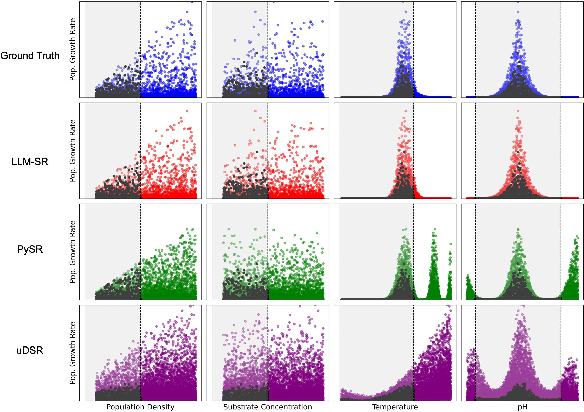
Mathematical equations have been unreasonably effective in describing complex natural phenomena across various scientific disciplines. However, discovering such insightful equations from data presents significant challenges due to the necessity of navigating extremely high-dimensional combinatorial and nonlinear hypothesis spaces. Traditional methods of equation discovery largely focus on extracting equations from data alone, often neglecting the rich domain-specific prior knowledge that scientists typically depend on. To bridge this gap, we introduce LLM-SR, a novel approach that leverages the extensive scientific knowledge and robust code generation capabilities of Large Language Models (LLMs) to discover scientific equations from data in an efficient manner. Specifically, LLM-SR treats equations as programs with mathematical operators and combines LLMs' scientific priors with evolutionary search over equation programs. The LLM iteratively proposes new equation skeletons, drawing from its physical understanding, which are then optimized against data to estimate skeleton parameters. We demonstrate LLM-SR's effectiveness across three diverse scientific domains, where it discovers physically accurate equations that provide significantly better fits to in-domain and out-of-domain data compared to the well-established equation discovery baselines

Graph-based Multi-ODE Neural Networks for Spatio-Temporal Traffic Forecasting

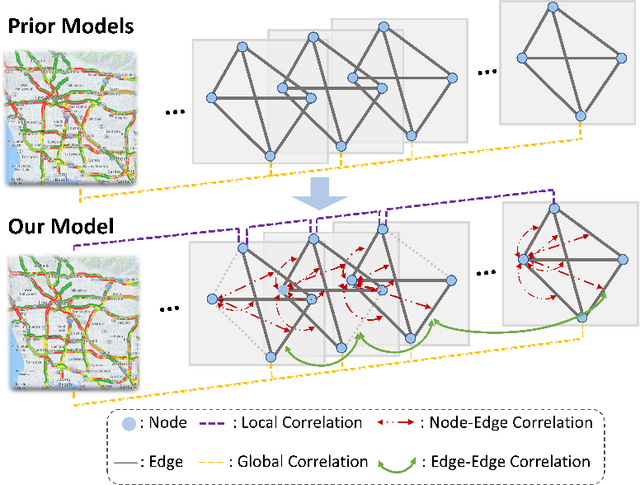
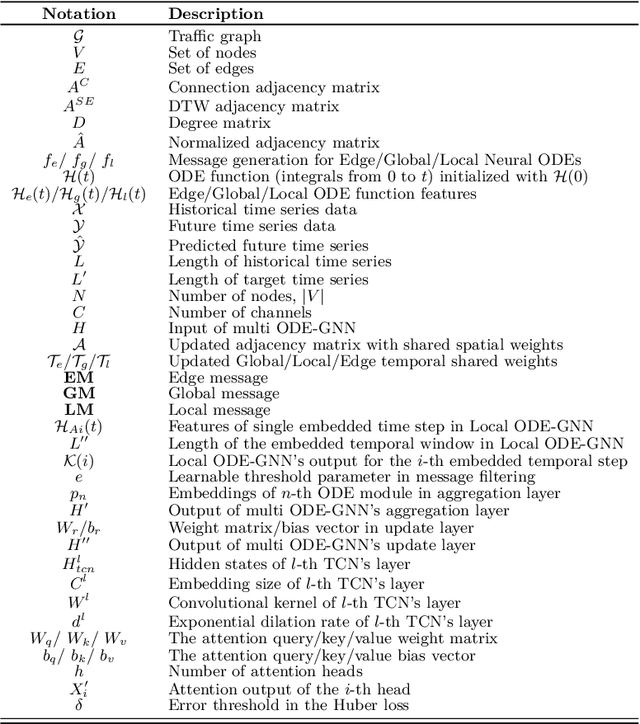
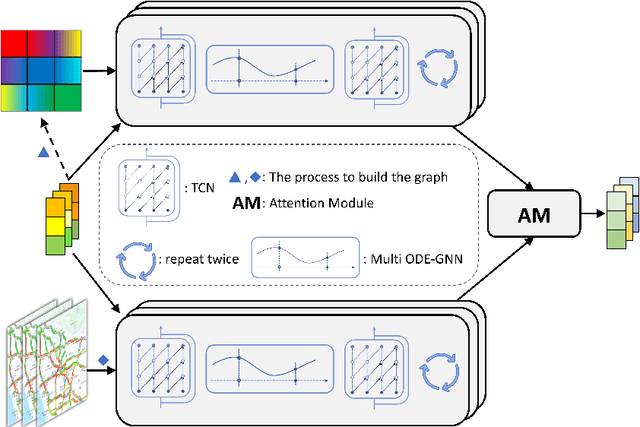
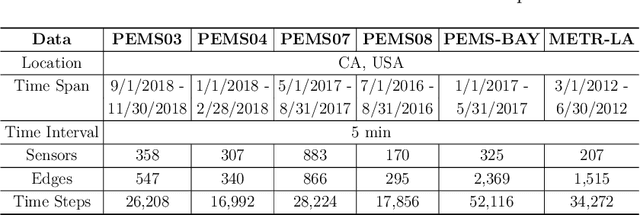
There is a recent surge in the development of spatio-temporal forecasting models in the transportation domain. Long-range traffic forecasting, however, remains a challenging task due to the intricate and extensive spatio-temporal correlations observed in traffic networks. Current works primarily rely on road networks with graph structures and learn representations using graph neural networks (GNNs), but this approach suffers from over-smoothing problem in deep architectures. To tackle this problem, recent methods introduced the combination of GNNs with residual connections or neural ordinary differential equations (ODE). However, current graph ODE models face two key limitations in feature extraction: (1) they lean towards global temporal patterns, overlooking local patterns that are important for unexpected events; and (2) they lack dynamic semantic edges in their architectural design. In this paper, we propose a novel architecture called Graph-based Multi-ODE Neural Networks (GRAM-ODE) which is designed with multiple connective ODE-GNN modules to learn better representations by capturing different views of complex local and global dynamic spatio-temporal dependencies. We also add some techniques like shared weights and divergence constraints into the intermediate layers of distinct ODE-GNN modules to further improve their communication towards the forecasting task. Our extensive set of experiments conducted on six real-world datasets demonstrate the superior performance of GRAM-ODE compared with state-of-the-art baselines as well as the contribution of different components to the overall performance. The code is available at https://github.com/zbliu98/GRAM-ODE

WindowSHAP: An Efficient Framework for Explaining Time-series Classifiers based on Shapley Values

Unpacking and comprehending how deep learning algorithms make decisions has been a persistent challenge for researchers and end-users. Explaining time-series predictive models is useful for clinical applications with high stakes to understand the behavior of prediction models. However, existing approaches to explain such models are frequently unique to architectures and data where the features do not have a time-varying component. In this paper, we introduce WindowSHAP, a model-agnostic framework for explaining time-series classifiers using Shapley values. We intend for WindowSHAP to mitigate the computational complexity of calculating Shapley values for long time-series data as well as improve the quality of explanations. WindowSHAP is based on partitioning a sequence into time windows. Under this framework, we present three distinct algorithms of Stationary, Sliding and Dynamic WindowSHAP, each evaluated against baseline approaches, KernelSHAP and TimeSHAP, using perturbation and sequence analyses metrics. We applied our framework to clinical time-series data from both a specialized clinical domain (Traumatic Brain Injury - TBI) as well as a broad clinical domain (critical care medicine). The experimental results demonstrate that, based on the two quantitative metrics, our framework is superior at explaining clinical time-series classifiers, while also reducing the complexity of computations. We show that for time-series data with 120 time steps (hours), merging 10 adjacent time points can reduce the CPU time of WindowSHAP by 80% compared to KernelSHAP. We also show that our Dynamic WindowSHAP algorithm focuses more on the most important time steps and provides more understandable explanations. As a result, WindowSHAP not only accelerates the calculation of Shapley values for time-series data, but also delivers more understandable explanations with higher quality.