Amirreza Hashemi
Equivariant Spherical CNN for Data Efficient and High-Performance Medical Image Processing
Jul 06, 2023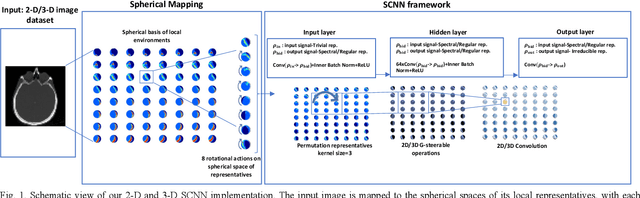
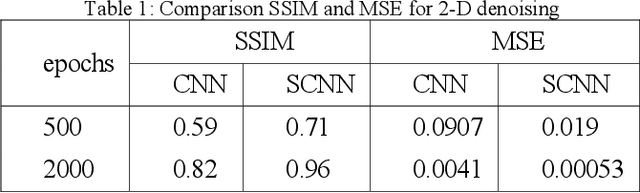
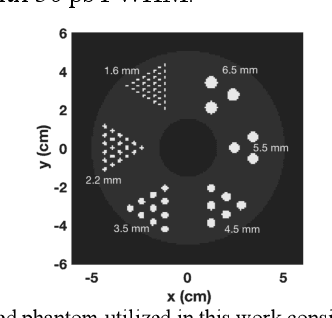
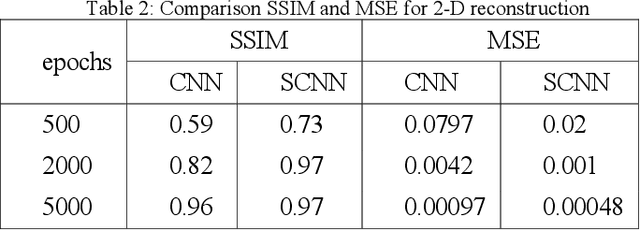
Abstract:This work highlights the significance of equivariant networks as efficient and high-performance approaches for tomography applications. Our study builds upon the limitations of Convolutional Neural Networks (CNNs), which have shown promise in post-processing various medical imaging systems. However, the efficiency of conventional CNNs heavily relies on an undiminished and proper training set. To tackle this issue, in this study, we introduce an equivariant network, aiming to reduce CNN's dependency on specific training sets. We evaluate the efficacy of equivariant CNNs on spherical signals for tomographic medical imaging problems. Our results demonstrate superior quality and computational efficiency of spherical CNNs (SCNNs) in denoising and reconstructing benchmark problems. Furthermore, we propose a novel approach to employ SCNNs as a complement to conventional image reconstruction tools, enhancing the outcomes while reducing reliance on the training set. Across all cases, we observe a significant decrease in computational costs while maintaining the same or higher quality of image processing using SCNNs compared to CNNs. Additionally, we explore the potential of this network for broader tomography applications, particularly those requiring omnidirectional representation.
Graph Convolutional Neural Networks for Body Force Prediction
Dec 03, 2020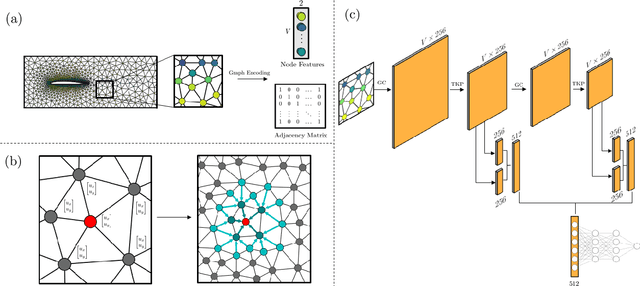


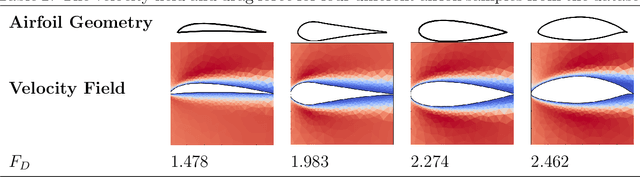
Abstract:Many scientific and engineering processes produce spatially unstructured data. However, most data-driven models require a feature matrix that enforces both a set number and order of features for each sample. They thus cannot be easily constructed for an unstructured dataset. Therefore, a graph based data-driven model to perform inference on fields defined on an unstructured mesh, using a Graph Convolutional Neural Network (GCNN) is presented. The ability of the method to predict global properties from spatially irregular measurements with high accuracy is demonstrated by predicting the drag force associated with laminar flow around airfoils from scattered velocity measurements. The network can infer from field samples at different resolutions, and is invariant to the order in which the measurements within each sample are presented. The GCNN method, using inductive convolutional layers and adaptive pooling, is able to predict this quantity with a validation $R^{2}$ above 0.98, and a Normalized Mean Squared Error below 0.01, without relying on spatial structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge