Segmentation of cracks in 3d images of fiber reinforced concrete using deep learning

Cracks in concrete structures are very common and are an integral part of this heterogeneous material. Characteristics of cracks induced by standardized tests yield valuable information about the tested concrete formulation and its mechanical properties. Observing cracks on the surface of the concrete structure leaves a wealth of structural information unused. Computed tomography enables looking into the sample without interfering or destroying the microstructure. The reconstructed tomographic images are 3d images, consisting of voxels whose gray values represent local X-ray absorption. In order to identify voxels belonging to the crack, so to segment the crack structure in the images, appropriate algorithms need to be developed. Convolutional neural networks are known to solve this type of task very well given enough and consistent training data. We adapted a 3d version of the well-known U-Net and trained it on semi-synthetic 3d images of real concrete samples equipped with simulated crack structures. Here, we explain the general approach. Moreover, we show how to teach the network to detect also real crack systems in 3d images of varying types of real concrete, in particular of fiber reinforced concrete.

Simulation of microstructures and machine learning

Machine learning offers attractive solutions to challenging image processing tasks. Tedious development and parametrization of algorithmic solutions can be replaced by training a convolutional neural network or a random forest with a high potential to generalize. However, machine learning methods rely on huge amounts of representative image data along with a ground truth, usually obtained by manual annotation. Thus, limited availability of training data is a critical bottleneck. We discuss two use cases: optical quality control in industrial production and segmenting crack structures in 3D images of concrete. For optical quality control, all defect types have to be trained but are typically not evenly represented in the training data. Additionally, manual annotation is costly and often inconsistent. It is nearly impossible in the second case: segmentation of crack systems in 3D images of concrete. Synthetic images, generated based on realizations of stochastic geometry models, offer an elegant way out. A wide variety of structure types can be generated. The within structure variation is naturally captured by the stochastic nature of the models and the ground truth is for free. Many new questions arise. In particular, which characteristics of the real image data have to be met to which degree of fidelity.

Cracks in concrete

Finding and properly segmenting cracks in images of concrete is a challenging task. Cracks are thin and rough and being air filled do yield a very weak contrast in 3D images obtained by computed tomography. Enhancing and segmenting dark lower-dimensional structures is already demanding. The heterogeneous concrete matrix and the size of the images further increase the complexity. ML methods have proven to solve difficult segmentation problems when trained on enough and well annotated data. However, so far, there is not much 3D image data of cracks available at all, let alone annotated. Interactive annotation is error-prone as humans can easily tell cats from dogs or roads without from roads with cars but have a hard time deciding whether a thin and dark structure seen in a 2D slice continues in the next one. Training networks by synthetic, simulated images is an elegant way out, bears however its own challenges. In this contribution, we describe how to generate semi-synthetic image data to train CNN like the well known 3D U-Net or random forests for segmenting cracks in 3D images of concrete. The thickness of real cracks varies widely, both, within one crack as well as from crack to crack in the same sample. The segmentation method should therefore be invariant with respect to scale changes. We introduce the so-called RieszNet, designed for exactly this purpose. Finally, we discuss how to generalize the ML crack segmentation methods to other concrete types.

MorphFlow: Estimating Motion in In Situ Tests of Concrete

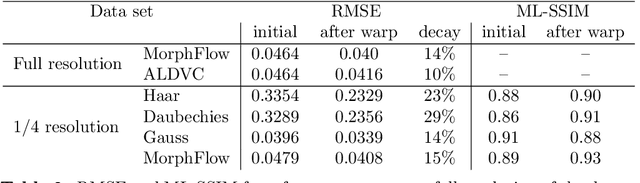
We present a novel algorithm explicitly tailored to estimate motion from time series of 3D images of concrete. Such volumetric images are usually acquired by Computed Tomography and can contain for example in situ tests, or more complex procedures like self-healing. Our algorithm is specifically designed to tackle the challenge of large scale in situ investigations of concrete. That means it cannot only cope with big images, but also with discontinuous displacement fields that often occur in in situ tests of concrete. We show the superior performance of our algorithm, especially regarding plausibility and time efficient processing. Core of the algorithm is a novel multiscale representation based on morphological wavelets. We use two examples for validation: A classical in situ test on refractory concrete and and a three point bending test on normal concrete. We show that for both applications structural changes like crack initiation can be already found at low scales -- a central achievement of our algorithm.

Hybrid quantum transfer learning for crack image classification on NISQ hardware

Quantum computers possess the potential to process data using a remarkably reduced number of qubits compared to conventional bits, as per theoretical foundations. However, recent experiments have indicated that the practical feasibility of retrieving an image from its quantum encoded version is currently limited to very small image sizes. Despite this constraint, variational quantum machine learning algorithms can still be employed in the current noisy intermediate scale quantum (NISQ) era. An example is a hybrid quantum machine learning approach for edge detection. In our study, we present an application of quantum transfer learning for detecting cracks in gray value images. We compare the performance and training time of PennyLane's standard qubits with IBM's qasm\_simulator and real backends, offering insights into their execution efficiency.

Riesz feature representation: scale equivariant scattering network for classification tasks

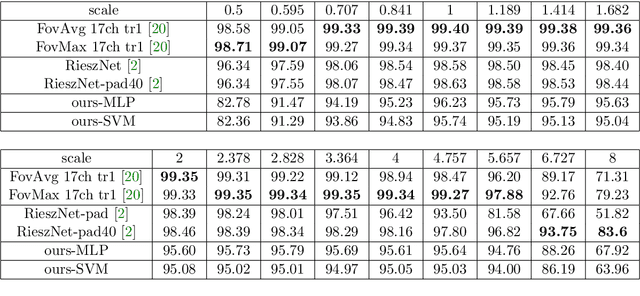
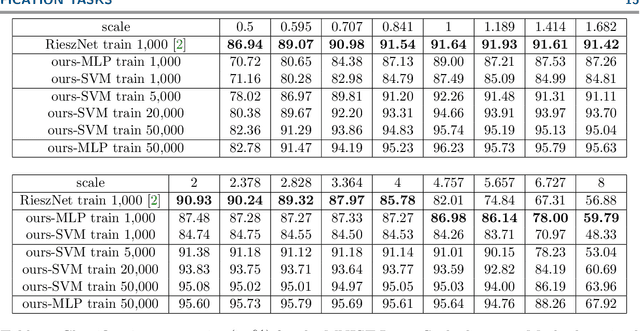
Scattering networks yield powerful and robust hierarchical image descriptors which do not require lengthy training and which work well with very few training data. However, they rely on sampling the scale dimension. Hence, they become sensitive to scale variations and are unable to generalize to unseen scales. In this work, we define an alternative feature representation based on the Riesz transform. We detail and analyze the mathematical foundations behind this representation. In particular, it inherits scale equivariance from the Riesz transform and completely avoids sampling of the scale dimension. Additionally, the number of features in the representation is reduced by a factor four compared to scattering networks. Nevertheless, our representation performs comparably well for texture classification with an interesting addition: scale equivariance. Our method yields superior performance when dealing with scales outside of those covered by the training dataset. The usefulness of the equivariance property is demonstrated on the digit classification task, where accuracy remains stable even for scales four times larger than the one chosen for training. As a second example, we consider classification of textures.

Riesz networks: scale invariant neural networks in a single forward pass

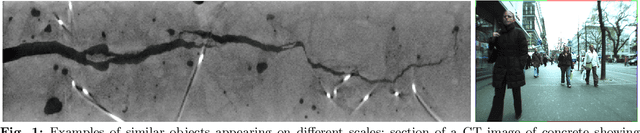
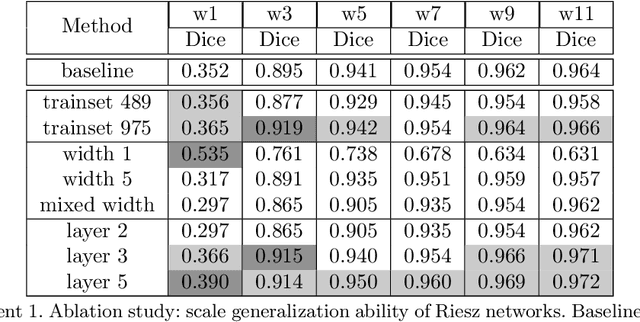
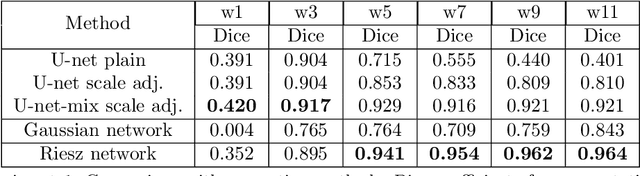
Scale invariance of an algorithm refers to its ability to treat objects equally independently of their size. For neural networks, scale invariance is typically achieved by data augmentation. However, when presented with a scale far outside the range covered by the training set, neural networks may fail to generalize. Here, we introduce the Riesz network, a novel scale invariant neural network. Instead of standard 2d or 3d convolutions for combining spatial information, the Riesz network is based on the Riesz transform which is a scale equivariant operation. As a consequence, this network naturally generalizes to unseen or even arbitrary scales in a single forward pass. As an application example, we consider detecting and segmenting cracks in tomographic images of concrete. In this context, 'scale' refers to the crack thickness which may vary strongly even within the same sample. To prove its scale invariance, the Riesz network is trained on one fixed crack width. We then validate its performance in segmenting simulated and real tomographic images featuring a wide range of crack widths. An additional experiment is carried out on the MNIST Large Scale data set.

Improved Anisotropic Gaussian Filters

Elongated anisotropic Gaussian filters are used for the orientation estimation of fibers. In cases where computed tomography images are noisy, roughly resolved, and of low contrast, they are the method of choice even if being efficient only in virtual 2D slices. However, minor inaccuracies in the anisotropic Gaussian filters can carry over to the orientation estimation. Therefore, we propose a modified algorithm for 2D anisotropic Gaussian filters and show that this improves their precision. Applied to synthetic images of fiber bundles, it is more accurate and robust to noise. Finally, we demonstrate the effectiveness of our approach by applying it to real-world images of sheet molding compounds.

Assessing cloudiness in nonwovens

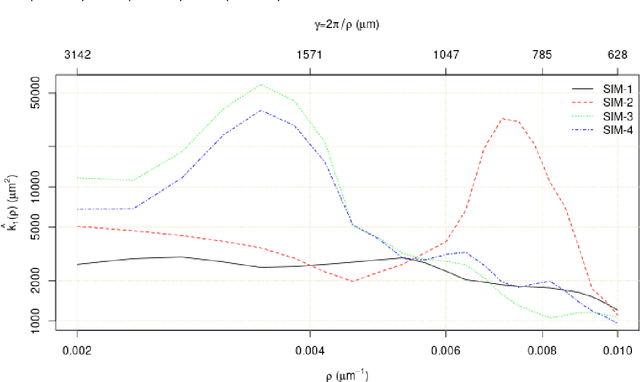
The homogeneity of filter media is important for material selection and quality control, along with the specific weight (nominal grammage) and the distribution of the local weight. Cloudiness or formation is a concept used to describe deviations from homogeneity in filter media. We suggest to derive the cloudiness index from the power spectrum of the relative local areal weight, integrated over a selected frequency range. The power spectrum captures the energy density in a broad spectral range. Moreover, under certain conditions, the structure of a nonwoven is fully characterized by the areal weight, the variance of the local areal weight, and the power spectrum. Consequently, the power spectrum is the parameter that exclusively reflects the cloudiness. Here, we address questions arising from practical application. The most prominent is the choice of the spectral band. It certainly depends on the characteristic "size of the clouds", but is limited by the size and lateral resolution of the images. We show that the cloudiness index based on the power spectrum of the relative local areal weight is theoretically well founded and can be robustly measured from image data. Choosing the spectral band allows to capture the cloudiness either visually perceived or found to be decisive for product properties. It is thus well suited to build a technical standard on it.

A hybrid quantum image edge detector for the NISQ era

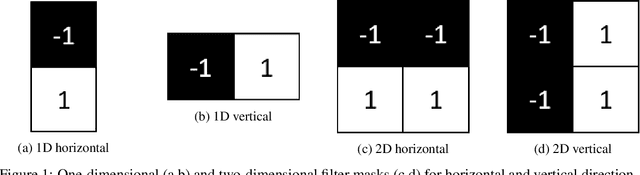
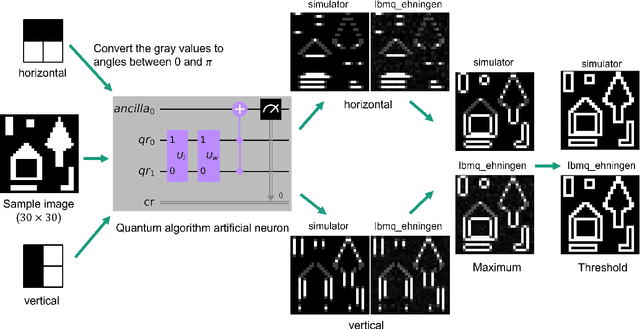
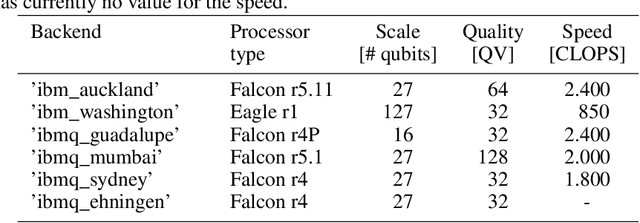
Edges are image locations where the gray value intensity changes suddenly. They are among the most important features to understand and segment an image. Edge detection is a standard task in digital image processing, solved for example using filtering techniques. However, the amount of data to be processed grows rapidly and pushes even supercomputers to their limits. Quantum computing promises exponentially lower memory usage in terms of the number of qubits compared to the number of classical bits. In this paper, we propose a hybrid method for quantum edge detection based on the idea of a quantum artificial neuron. Our method can be practically implemented on quantum computers, especially on those of the current noisy intermediate-scale quantum era. We compare six variants of the method to reduce the number of circuits and thus the time required for the quantum edge detection. Taking advantage of the scalability of our method, we can practically detect edges in images considerably larger than reached before.