Improved Anisotropic Gaussian Filters

Elongated anisotropic Gaussian filters are used for the orientation estimation of fibers. In cases where computed tomography images are noisy, roughly resolved, and of low contrast, they are the method of choice even if being efficient only in virtual 2D slices. However, minor inaccuracies in the anisotropic Gaussian filters can carry over to the orientation estimation. Therefore, we propose a modified algorithm for 2D anisotropic Gaussian filters and show that this improves their precision. Applied to synthetic images of fiber bundles, it is more accurate and robust to noise. Finally, we demonstrate the effectiveness of our approach by applying it to real-world images of sheet molding compounds.

Assessing cloudiness in nonwovens

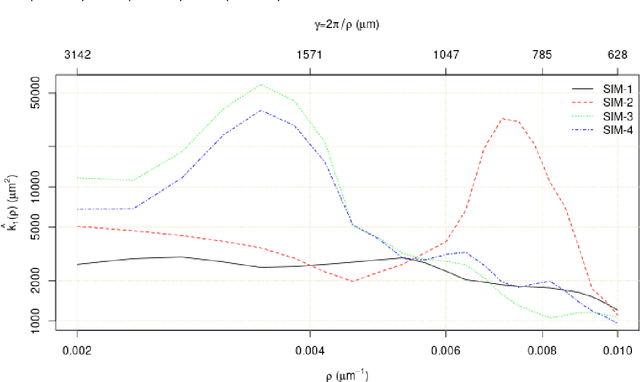
The homogeneity of filter media is important for material selection and quality control, along with the specific weight (nominal grammage) and the distribution of the local weight. Cloudiness or formation is a concept used to describe deviations from homogeneity in filter media. We suggest to derive the cloudiness index from the power spectrum of the relative local areal weight, integrated over a selected frequency range. The power spectrum captures the energy density in a broad spectral range. Moreover, under certain conditions, the structure of a nonwoven is fully characterized by the areal weight, the variance of the local areal weight, and the power spectrum. Consequently, the power spectrum is the parameter that exclusively reflects the cloudiness. Here, we address questions arising from practical application. The most prominent is the choice of the spectral band. It certainly depends on the characteristic "size of the clouds", but is limited by the size and lateral resolution of the images. We show that the cloudiness index based on the power spectrum of the relative local areal weight is theoretically well founded and can be robustly measured from image data. Choosing the spectral band allows to capture the cloudiness either visually perceived or found to be decisive for product properties. It is thus well suited to build a technical standard on it.

An unambiguous cloudiness index for nonwovens

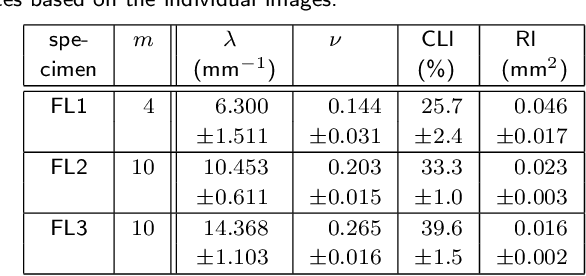
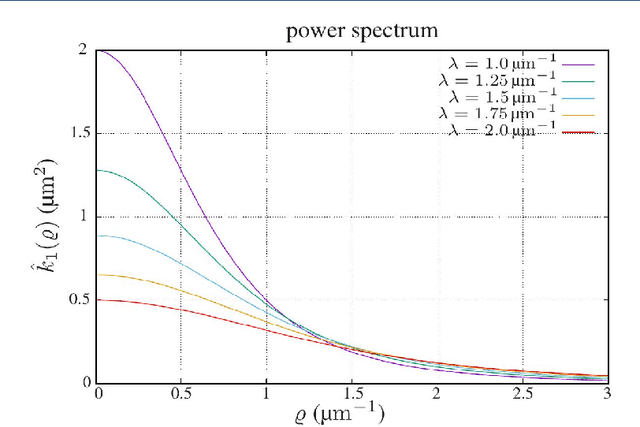
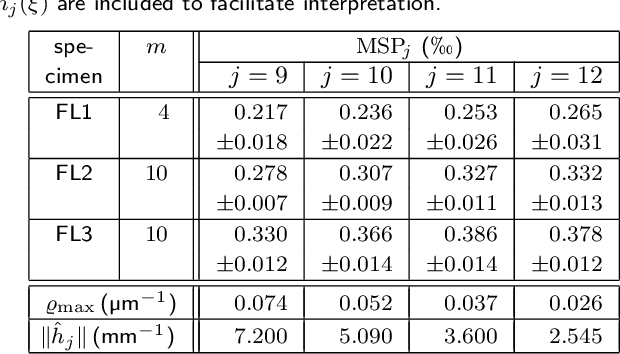
Cloudiness or formation is a concept routinely used in industry to address deviations from homogeneity in nonwovens and papers. Measuring a cloudiness index based on image data is a common task in industrial quality assurance. The two most popular ways of quantifying cloudiness are based on power spectrum or correlation function on the one hand or the Laplacian pyramid on the other hand. Here, we recall the mathematical basis of the first approach comprehensively, derive a cloudiness index, and demonstrate its practical estimation. We prove that the Laplacian pyramid as well as other quantities characterizing cloudiness like the range of interaction and the intensity of small-angle scattering are very closely related to the power spectrum. Finally, we show that the power spectrum is easy to be measured image analytically and carries more information than the alternatives.