Benefiting from Quantum? A Comparative Study of Q-Seg, Quantum-Inspired Techniques, and U-Net for Crack Segmentation

Exploring the potential of quantum hardware for enhancing classical and real-world applications is an ongoing challenge. This study evaluates the performance of quantum and quantum-inspired methods compared to classical models for crack segmentation. Using annotated gray-scale image patches of concrete samples, we benchmark a classical mean Gaussian mixture technique, a quantum-inspired fermion-based method, Q-Seg a quantum annealing-based method, and a U-Net deep learning architecture. Our results indicate that quantum-inspired and quantum methods offer a promising alternative for image segmentation, particularly for complex crack patterns, and could be applied in near-future applications.

Variational Quantum Linear Solver enhanced Quantum Support Vector Machine

Quantum Support Vector Machines (QSVM) play a vital role in using quantum resources for supervised machine learning tasks, such as classification. However, current methods are strongly limited in terms of scalability on Noisy Intermediate Scale Quantum (NISQ) devices. In this work, we propose a novel approach called the Variational Quantum Linear Solver (VQLS) enhanced QSVM. This is built upon our idea of utilizing the variational quantum linear solver to solve system of linear equations of a least squares-SVM on a NISQ device. The implementation of our approach is evaluated by an extensive series of numerical experiments with the Iris dataset, which consists of three distinct iris plant species. Based on this, we explore the practicality and effectiveness of our algorithm by constructing a classifier capable of classification in a feature space ranging from one to seven dimensions. Furthermore, by strategically exploiting both classical and quantum computing for various subroutines of our algorithm, we effectively mitigate practical challenges associated with the implementation. These include significant improvement in the trainability of the variational ansatz and notable reductions in run-time for cost calculations. Based on the numerical experiments, our approach exhibits the capability of identifying a separating hyperplane in an 8-dimensional feature space. Moreover, it consistently demonstrated strong performance across various instances with the same dataset.

Hybrid quantum transfer learning for crack image classification on NISQ hardware

Quantum computers possess the potential to process data using a remarkably reduced number of qubits compared to conventional bits, as per theoretical foundations. However, recent experiments have indicated that the practical feasibility of retrieving an image from its quantum encoded version is currently limited to very small image sizes. Despite this constraint, variational quantum machine learning algorithms can still be employed in the current noisy intermediate scale quantum (NISQ) era. An example is a hybrid quantum machine learning approach for edge detection. In our study, we present an application of quantum transfer learning for detecting cracks in gray value images. We compare the performance and training time of PennyLane's standard qubits with IBM's qasm\_simulator and real backends, offering insights into their execution efficiency.

Improved Anisotropic Gaussian Filters

Elongated anisotropic Gaussian filters are used for the orientation estimation of fibers. In cases where computed tomography images are noisy, roughly resolved, and of low contrast, they are the method of choice even if being efficient only in virtual 2D slices. However, minor inaccuracies in the anisotropic Gaussian filters can carry over to the orientation estimation. Therefore, we propose a modified algorithm for 2D anisotropic Gaussian filters and show that this improves their precision. Applied to synthetic images of fiber bundles, it is more accurate and robust to noise. Finally, we demonstrate the effectiveness of our approach by applying it to real-world images of sheet molding compounds.

Assessing cloudiness in nonwovens

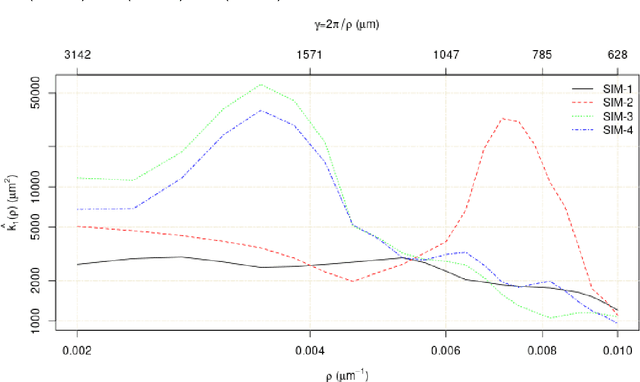
The homogeneity of filter media is important for material selection and quality control, along with the specific weight (nominal grammage) and the distribution of the local weight. Cloudiness or formation is a concept used to describe deviations from homogeneity in filter media. We suggest to derive the cloudiness index from the power spectrum of the relative local areal weight, integrated over a selected frequency range. The power spectrum captures the energy density in a broad spectral range. Moreover, under certain conditions, the structure of a nonwoven is fully characterized by the areal weight, the variance of the local areal weight, and the power spectrum. Consequently, the power spectrum is the parameter that exclusively reflects the cloudiness. Here, we address questions arising from practical application. The most prominent is the choice of the spectral band. It certainly depends on the characteristic "size of the clouds", but is limited by the size and lateral resolution of the images. We show that the cloudiness index based on the power spectrum of the relative local areal weight is theoretically well founded and can be robustly measured from image data. Choosing the spectral band allows to capture the cloudiness either visually perceived or found to be decisive for product properties. It is thus well suited to build a technical standard on it.

A hybrid quantum image edge detector for the NISQ era

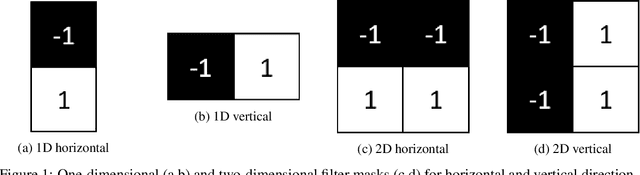
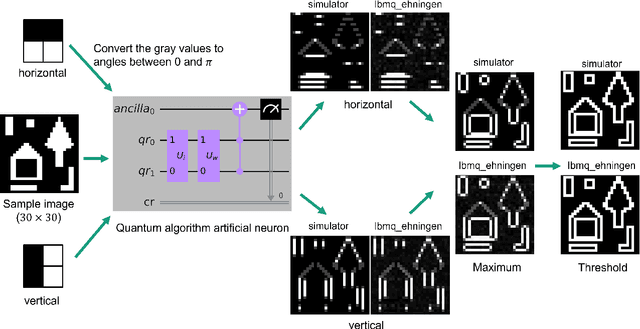
Edges are image locations where the gray value intensity changes suddenly. They are among the most important features to understand and segment an image. Edge detection is a standard task in digital image processing, solved for example using filtering techniques. However, the amount of data to be processed grows rapidly and pushes even supercomputers to their limits. Quantum computing promises exponentially lower memory usage in terms of the number of qubits compared to the number of classical bits. In this paper, we propose a hybrid method for quantum edge detection based on the idea of a quantum artificial neuron. Our method can be practically implemented on quantum computers, especially on those of the current noisy intermediate-scale quantum era. We compare six variants of the method to reduce the number of circuits and thus the time required for the quantum edge detection. Taking advantage of the scalability of our method, we can practically detect edges in images considerably larger than reached before.

An unambiguous cloudiness index for nonwovens

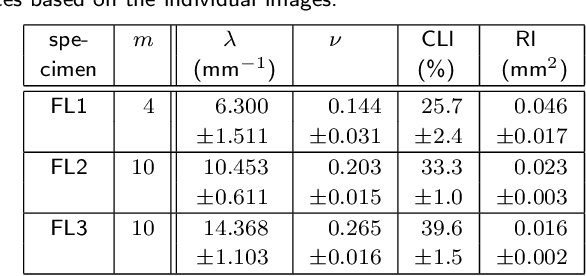
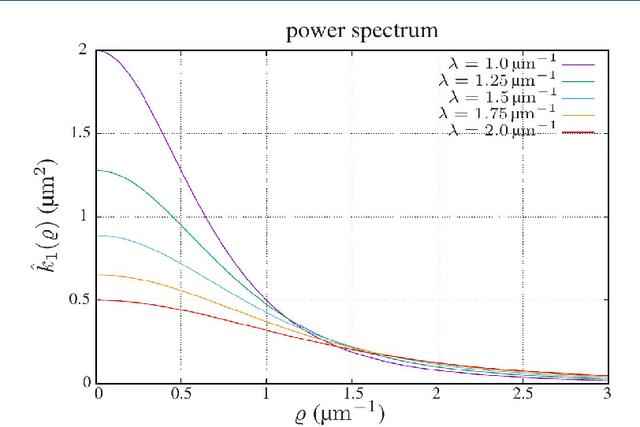
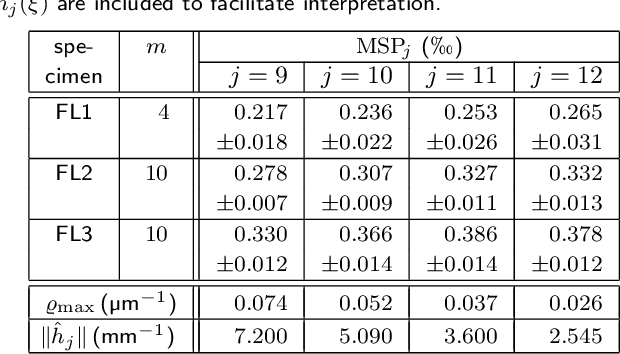
Cloudiness or formation is a concept routinely used in industry to address deviations from homogeneity in nonwovens and papers. Measuring a cloudiness index based on image data is a common task in industrial quality assurance. The two most popular ways of quantifying cloudiness are based on power spectrum or correlation function on the one hand or the Laplacian pyramid on the other hand. Here, we recall the mathematical basis of the first approach comprehensively, derive a cloudiness index, and demonstrate its practical estimation. We prove that the Laplacian pyramid as well as other quantities characterizing cloudiness like the range of interaction and the intensity of small-angle scattering are very closely related to the power spectrum. Finally, we show that the power spectrum is easy to be measured image analytically and carries more information than the alternatives.

Improved FRQI on superconducting processors and its restrictions in the NISQ era

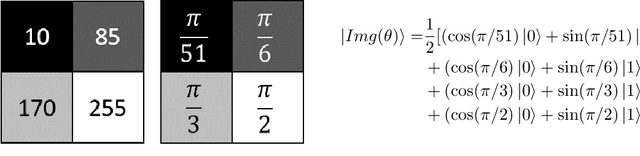
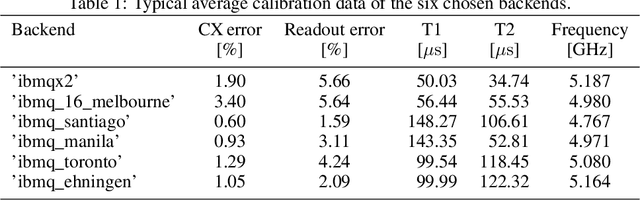
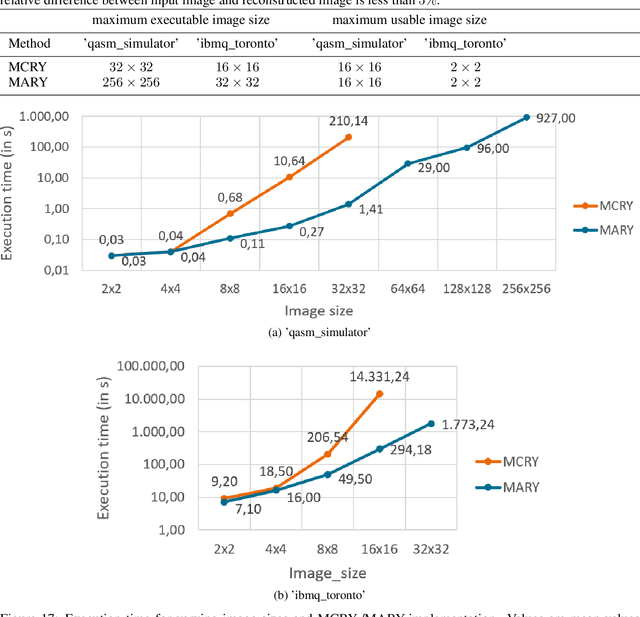
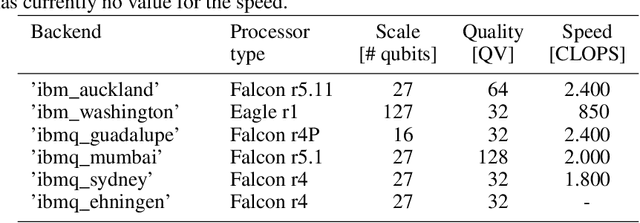
In image processing, the amount of data to be processed grows rapidly, in particular when imaging methods yield images of more than two dimensions or time series of images. Thus, efficient processing is a challenge, as data sizes may push even supercomputers to their limits. Quantum image processing promises to encode images with logarithmically less qubits than classical pixels in the image. In theory, this is a huge progress, but so far not many experiments have been conducted in practice, in particular on real backends. Often, the precise conversion of classical data to quantum states, the exact implementation, and the interpretation of the measurements in the classical context are challenging. We investigate these practical questions in this paper. In particular, we study the feasibility of the Flexible Representation of Quantum Images (FRQI). Furthermore, we check experimentally what is the limit in the current noisy intermediate-scale quantum era, i.e. up to which image size an image can be encoded, both on simulators and on real backends. Finally, we propose a method for simplifying the circuits needed for the FRQI. With our alteration, the number of gates needed, especially of the error-prone controlled-NOT gates, can be reduced. As a consequence, the size of manageable images increases.