Riesz feature representation: scale equivariant scattering network for classification tasks

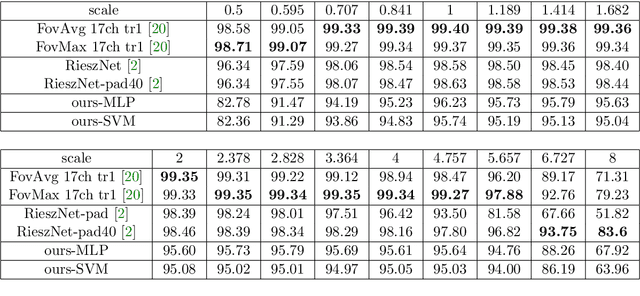
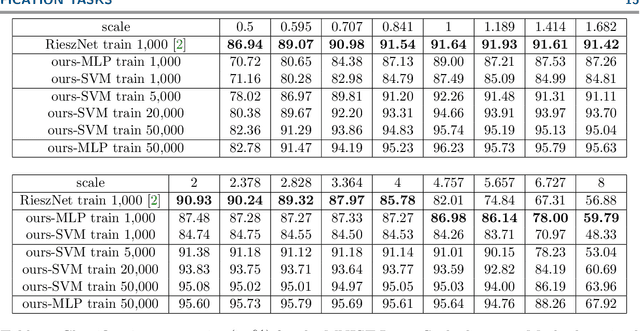
Scattering networks yield powerful and robust hierarchical image descriptors which do not require lengthy training and which work well with very few training data. However, they rely on sampling the scale dimension. Hence, they become sensitive to scale variations and are unable to generalize to unseen scales. In this work, we define an alternative feature representation based on the Riesz transform. We detail and analyze the mathematical foundations behind this representation. In particular, it inherits scale equivariance from the Riesz transform and completely avoids sampling of the scale dimension. Additionally, the number of features in the representation is reduced by a factor four compared to scattering networks. Nevertheless, our representation performs comparably well for texture classification with an interesting addition: scale equivariance. Our method yields superior performance when dealing with scales outside of those covered by the training dataset. The usefulness of the equivariance property is demonstrated on the digit classification task, where accuracy remains stable even for scales four times larger than the one chosen for training. As a second example, we consider classification of textures.

Adapting the Hypersphere Loss Function from Anomaly Detection to Anomaly Segmentation

We propose an incremental improvement to Fully Convolutional Data Description (FCDD), an adaptation of the one-class classification approach from anomaly detection to image anomaly segmentation (a.k.a. anomaly localization). We analyze its original loss function and propose a substitute that better resembles its predecessor, the Hypersphere Classifier (HSC). Both are compared on the MVTec Anomaly Detection Dataset (MVTec-AD) -- training images are flawless objects/textures and the goal is to segment unseen defects -- showing that consistent improvement is achieved by better designing the pixel-wise supervision.

Moving Frame Net: SE-Equivariant Network for Volumes

Equivariance of neural networks to transformations helps to improve their performance and reduce generalization error in computer vision tasks, as they apply to datasets presenting symmetries (e.g. scalings, rotations, translations). The method of moving frames is classical for deriving operators invariant to the action of a Lie group in a manifold.Recently, a rotation and translation equivariant neural network for image data was proposed based on the moving frames approach. In this paper we significantly improve that approach by reducing the computation of moving frames to only one, at the input stage, instead of repeated computations at each layer. The equivariance of the resulting architecture is proved theoretically and we build a rotation and translation equivariant neural network to process volumes, i.e. signals on the 3D space. Our trained model overperforms the benchmarks in the medical volume classification of most of the tested datasets from MedMNIST3D.

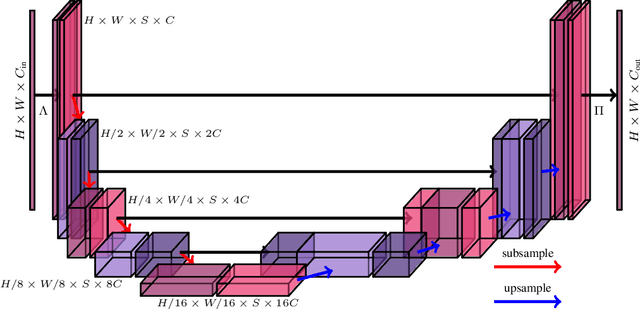
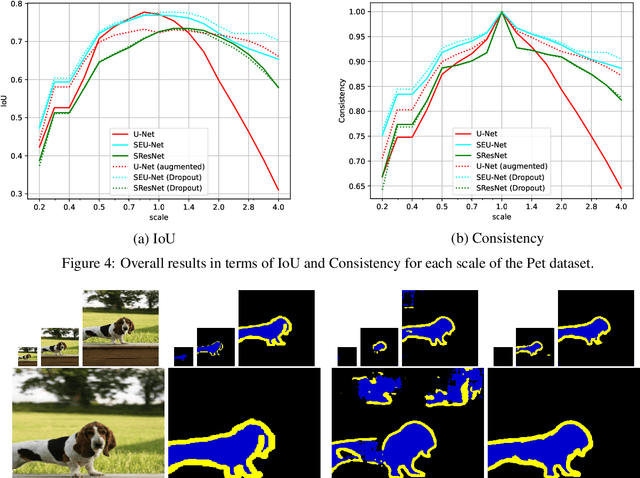
Scale Equivariant U-Net

In neural networks, the property of being equivariant to transformations improves generalization when the corresponding symmetry is present in the data. In particular, scale-equivariant networks are suited to computer vision tasks where the same classes of objects appear at different scales, like in most semantic segmentation tasks. Recently, convolutional layers equivariant to a semigroup of scalings and translations have been proposed. However, the equivariance of subsampling and upsampling has never been explicitly studied even though they are necessary building blocks in some segmentation architectures. The U-Net is a representative example of such architectures, which includes the basic elements used for state-of-the-art semantic segmentation. Therefore, this paper introduces the Scale Equivariant U-Net (SEU-Net), a U-Net that is made approximately equivariant to a semigroup of scales and translations through careful application of subsampling and upsampling layers and the use of aforementioned scale-equivariant layers. Moreover, a scale-dropout is proposed in order to improve generalization to different scales in approximately scale-equivariant architectures. The proposed SEU-Net is trained for semantic segmentation of the Oxford Pet IIIT and the DIC-C2DH-HeLa dataset for cell segmentation. The generalization metric to unseen scales is dramatically improved in comparison to the U-Net, even when the U-Net is trained with scale jittering, and to a scale-equivariant architecture that does not perform upsampling operators inside the equivariant pipeline. The scale-dropout induces better generalization on the scale-equivariant models in the Pet experiment, but not on the cell segmentation experiment.

Morphological adjunctions represented by matrices in max-plus algebra for signal and image processing

In discrete signal and image processing, many dilations and erosions can be written as the max-plus and min-plus product of a matrix on a vector. Previous studies considered operators on symmetrical, unbounded complete lattices, such as Cartesian powers of the completed real line. This paper focuses on adjunctions on closed hypercubes, which are the complete lattices used in practice to represent digital signals and images. We show that this constrains the representing matrices to be doubly-0-astic and we characterise the adjunctions that can be represented by them. A graph interpretation of the defined operators naturally arises from the adjacency relationship encoded by the matrices, as well as a max-plus spectral interpretation.

Fully trainable Gaussian derivative convolutional layer

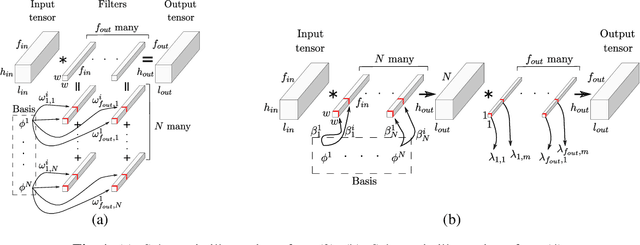
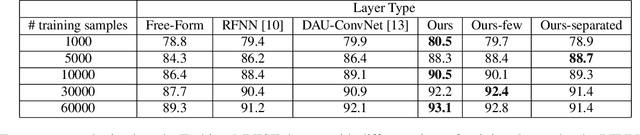
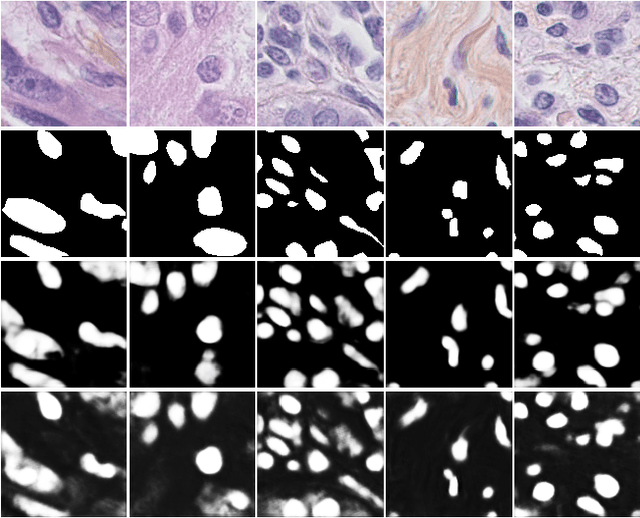
The Gaussian kernel and its derivatives have already been employed for Convolutional Neural Networks in several previous works. Most of these papers proposed to compute filters by linearly combining one or several bases of fixed or slightly trainable Gaussian kernels with or without their derivatives. In this article, we propose a high-level configurable layer based on anisotropic, oriented and shifted Gaussian derivative kernels which generalize notions encountered in previous related works while keeping their main advantage. The results show that the proposed layer has competitive performance compared to previous works and that it can be successfully included in common deep architectures such as VGG16 for image classification and U-net for image segmentation.

Near out-of-distribution detection for low-resolution radar micro-Doppler signatures

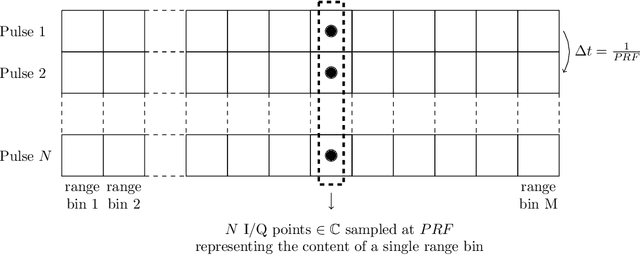
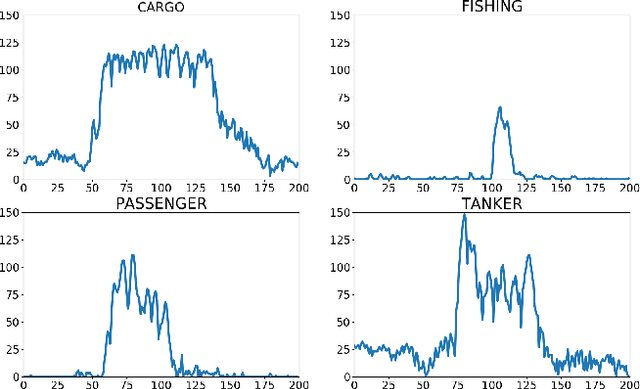
Near out-of-distribution detection (OOD) aims at discriminating semantically similar data points without the supervision required for classification. This paper puts forward an OOD use case for radar targets detection extensible to other kinds of sensors and detection scenarios. We emphasize the relevance of OOD and its specific supervision requirements for the detection of a multimodal, diverse targets class among other similar radar targets and clutter in real-life critical systems. We propose a comparison of deep and non-deep OOD methods on simulated low-resolution pulse radar micro-Doppler signatures, considering both a spectral and a covariance matrix input representation. The covariance representation aims at estimating whether dedicated second-order processing is appropriate to discriminate signatures. The potential contributions of labeled anomalies in training, self-supervised learning, contrastive learning insights and innovative training losses are discussed, and the impact of training set contamination caused by mislabelling is investigated.

Learning Deep Morphological Networks with Neural Architecture Search

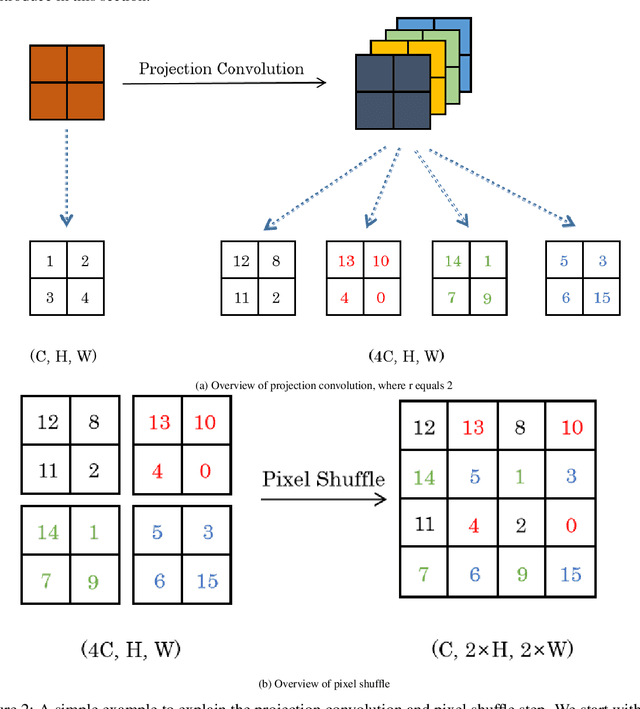
Deep Neural Networks (DNNs) are generated by sequentially performing linear and non-linear processes. Using a combination of linear and non-linear procedures is critical for generating a sufficiently deep feature space. The majority of non-linear operators are derivations of activation functions or pooling functions. Mathematical morphology is a branch of mathematics that provides non-linear operators for a variety of image processing problems. We investigate the utility of integrating these operations in an end-to-end deep learning framework in this paper. DNNs are designed to acquire a realistic representation for a particular job. Morphological operators give topological descriptors that convey salient information about the shapes of objects depicted in images. We propose a method based on meta-learning to incorporate morphological operators into DNNs. The learned architecture demonstrates how our novel morphological operations significantly increase DNN performance on various tasks, including picture classification and edge detection.

From Unsupervised to Semi-supervised Anomaly Detection Methods for HRRP Targets

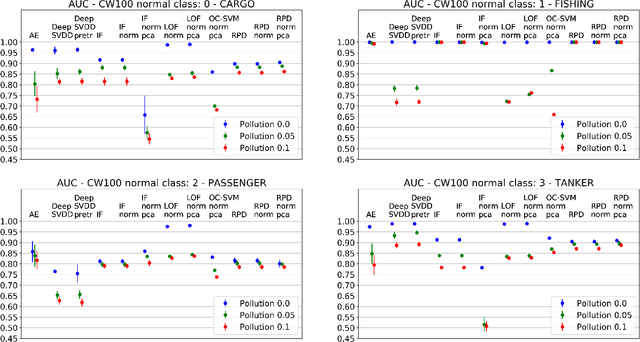
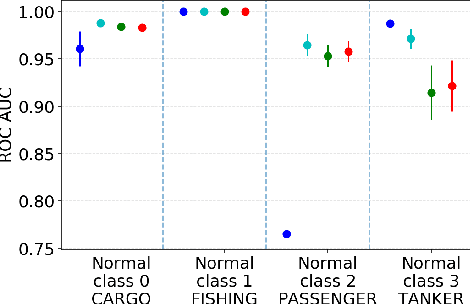
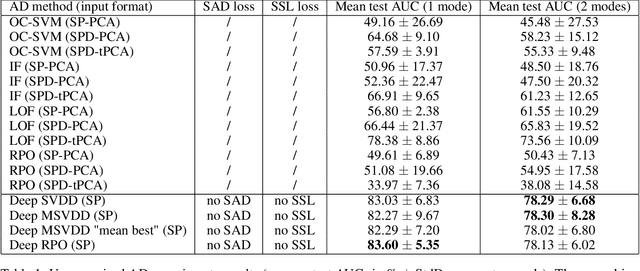
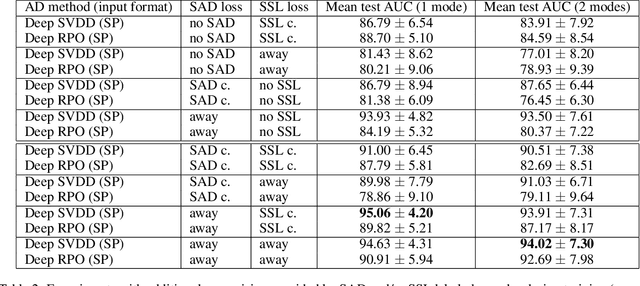
Responding to the challenge of detecting unusual radar targets in a well identified environment, innovative anomaly and novelty detection methods keep emerging in the literature. This work aims at presenting a benchmark gathering common and recently introduced unsupervised anomaly detection (AD) methods, the results being generated using high-resolution range profiles. A semi-supervised AD (SAD) is considered to demonstrate the added value of having a few labeled anomalies to improve performances. Experiments were conducted with and without pollution of the training set with anomalous samples in order to be as close as possible to real operational contexts. The common AD methods composing our baseline will be One-Class Support Vector Machines (OC-SVM), Isolation Forest (IF), Local Outlier Factor (LOF) and a Convolutional Autoencoder (CAE). The more innovative AD methods put forward by this work are Deep Support Vector Data Description (Deep SVDD) and Random Projection Depth (RPD), belonging respectively to deep and shallow AD. The semi-supervised adaptation of Deep SVDD constitutes our SAD method. HRRP data was generated by a coastal surveillance radar, our results thus suggest that AD can contribute to enhance maritime and coastal situation awareness.

Deep Random Projection Outlyingness for Unsupervised Anomaly Detection

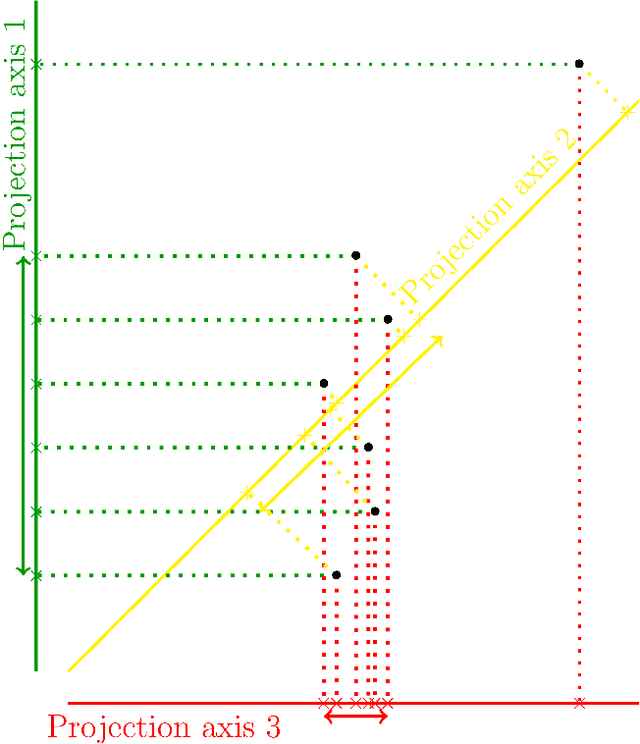
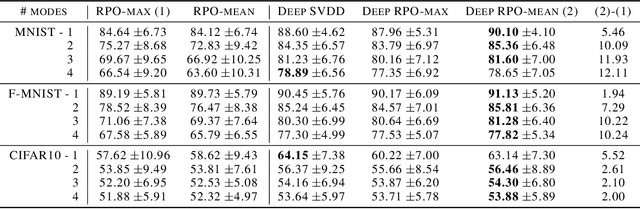
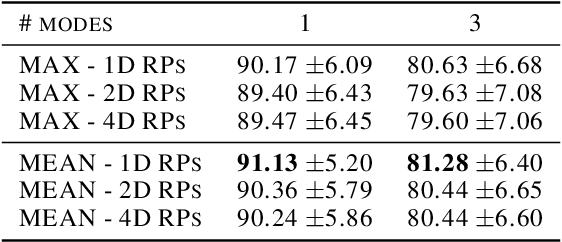
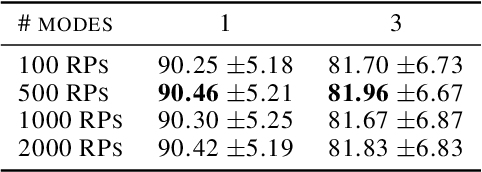
Random projection is a common technique for designing algorithms in a variety of areas, including information retrieval, compressive sensing and measuring of outlyingness. In this work, the original random projection outlyingness measure is modified and associated with a neural network to obtain an unsupervised anomaly detection method able to handle multimodal normality. Theoretical and experimental arguments are presented to justify the choices of the anomaly score estimator, the dimensions of the random projections, and the number of such projections. The contribution of adapted dropouts is investigated, along with the affine stability of the proposed method. The performance of the proposed neural network approach is comparable to a state-of-the-art anomaly detection method. Experiments conducted on the MNIST, Fashion-MNIST and CIFAR-10 datasets show the relevance of the proposed approach, and suggest a possible extension to a semi-supervised setup.