Moving Frame Net: SE-Equivariant Network for Volumes

Equivariance of neural networks to transformations helps to improve their performance and reduce generalization error in computer vision tasks, as they apply to datasets presenting symmetries (e.g. scalings, rotations, translations). The method of moving frames is classical for deriving operators invariant to the action of a Lie group in a manifold.Recently, a rotation and translation equivariant neural network for image data was proposed based on the moving frames approach. In this paper we significantly improve that approach by reducing the computation of moving frames to only one, at the input stage, instead of repeated computations at each layer. The equivariance of the resulting architecture is proved theoretically and we build a rotation and translation equivariant neural network to process volumes, i.e. signals on the 3D space. Our trained model overperforms the benchmarks in the medical volume classification of most of the tested datasets from MedMNIST3D.

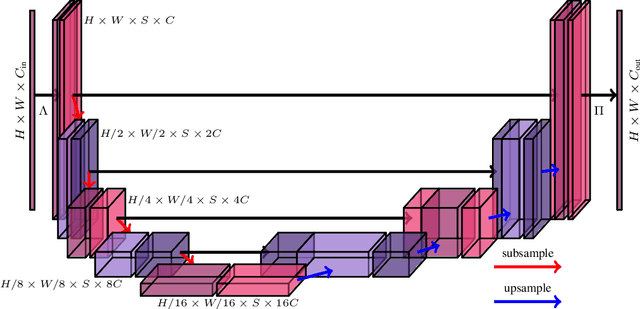
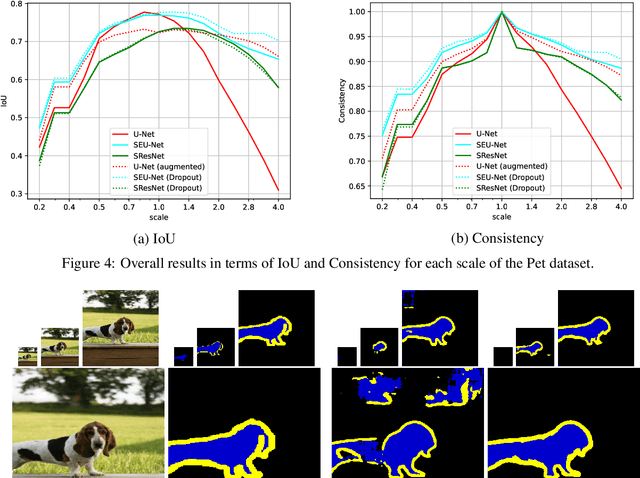
Scale Equivariant U-Net

In neural networks, the property of being equivariant to transformations improves generalization when the corresponding symmetry is present in the data. In particular, scale-equivariant networks are suited to computer vision tasks where the same classes of objects appear at different scales, like in most semantic segmentation tasks. Recently, convolutional layers equivariant to a semigroup of scalings and translations have been proposed. However, the equivariance of subsampling and upsampling has never been explicitly studied even though they are necessary building blocks in some segmentation architectures. The U-Net is a representative example of such architectures, which includes the basic elements used for state-of-the-art semantic segmentation. Therefore, this paper introduces the Scale Equivariant U-Net (SEU-Net), a U-Net that is made approximately equivariant to a semigroup of scales and translations through careful application of subsampling and upsampling layers and the use of aforementioned scale-equivariant layers. Moreover, a scale-dropout is proposed in order to improve generalization to different scales in approximately scale-equivariant architectures. The proposed SEU-Net is trained for semantic segmentation of the Oxford Pet IIIT and the DIC-C2DH-HeLa dataset for cell segmentation. The generalization metric to unseen scales is dramatically improved in comparison to the U-Net, even when the U-Net is trained with scale jittering, and to a scale-equivariant architecture that does not perform upsampling operators inside the equivariant pipeline. The scale-dropout induces better generalization on the scale-equivariant models in the Pet experiment, but not on the cell segmentation experiment.

Morphological adjunctions represented by matrices in max-plus algebra for signal and image processing

In discrete signal and image processing, many dilations and erosions can be written as the max-plus and min-plus product of a matrix on a vector. Previous studies considered operators on symmetrical, unbounded complete lattices, such as Cartesian powers of the completed real line. This paper focuses on adjunctions on closed hypercubes, which are the complete lattices used in practice to represent digital signals and images. We show that this constrains the representing matrices to be doubly-0-astic and we characterise the adjunctions that can be represented by them. A graph interpretation of the defined operators naturally arises from the adjacency relationship encoded by the matrices, as well as a max-plus spectral interpretation.

Differential invariants for SE(2)-equivariant networks

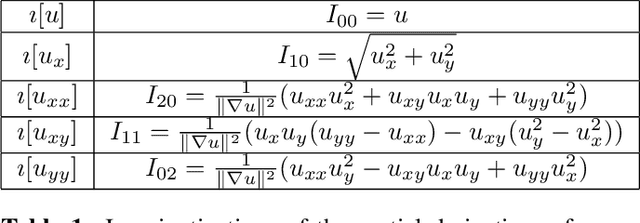
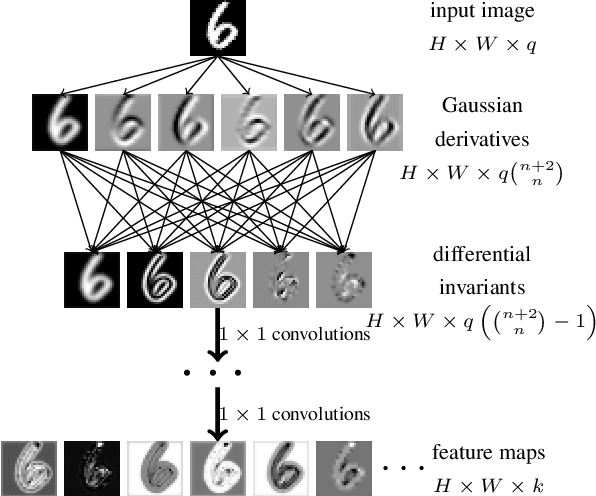
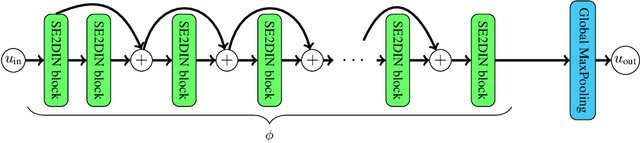
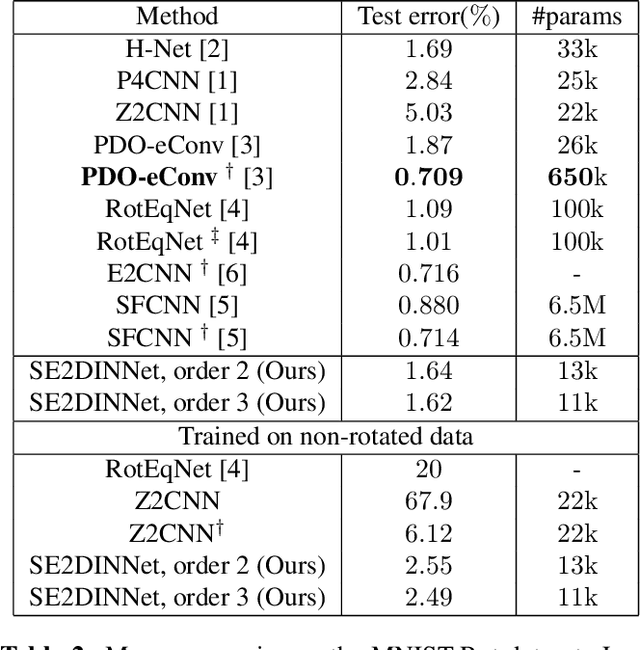
Symmetry is present in many tasks in computer vision, where the same class of objects can appear transformed, e.g. rotated due to different camera orientations, or scaled due to perspective. The knowledge of such symmetries in data coupled with equivariance of neural networks can improve their generalization to new samples. Differential invariants are equivariant operators computed from the partial derivatives of a function. In this paper we use differential invariants to define equivariant operators that form the layers of an equivariant neural network. Specifically, we derive invariants of the Special Euclidean Group SE(2), composed of rotations and translations, and apply them to construct a SE(2)-equivariant network, called SE(2) Differential Invariants Network (SE2DINNet). The network is subsequently tested in classification tasks which require a degree of equivariance or invariance to rotations. The results compare positively with the state-of-the-art, even though the proposed SE2DINNet has far less parameters than the compared models.

Scale Equivariant Neural Networks with Morphological Scale-Spaces

The translation equivariance of convolutions can make convolutional neural networks translation equivariant or invariant. Equivariance to other transformations (e.g. rotations, affine transformations, scalings) may also be desirable as soon as we know a priori that transformed versions of the same objects appear in the data. The semigroup cross-correlation, which is a linear operator equivariant to semigroup actions, was recently proposed and applied in conjunction with the Gaussian scale-space to create architectures which are equivariant to discrete scalings. In this paper, a generalization using a broad class of liftings, including morphological scale-spaces, is proposed. The architectures obtained from different scale-spaces are tested and compared in supervised classification and semantic segmentation tasks where objects in test images appear at different scales compared to training images. In both classification and segmentation tasks, the scale-equivariant architectures improve dramatically the generalization to unseen scales compared to a convolutional baseline. Besides, in our experiments morphological scale-spaces outperformed the Gaussian scale-space in geometrical tasks.

Max-plus Operators Applied to Filter Selection and Model Pruning in Neural Networks

Following recent advances in morphological neural networks, we propose to study in more depth how Max-plus operators can be exploited to define morphological units and how they behave when incorporated in layers of conventional neural networks. Besides showing that they can be easily implemented with modern machine learning frameworks , we confirm and extend the observation that a Max-plus layer can be used to select important filters and reduce redundancy in its previous layer, without incurring performance loss. Experimental results demonstrate that the filter selection strategy enabled by a Max-plus is highly efficient and robust, through which we successfully performed model pruning on different neural network architectures. We also point out that there is a close connection between Maxout networks and our pruned Max-plus networks by comparing their respective characteristics. The code for reproducing our experiments is available online.

Part-based approximations for morphological operators using asymmetric auto-encoders

This paper addresses the issue of building a part-based representation of a dataset of images. More precisely, we look for a non-negative, sparse decomposition of the images on a reduced set of atoms, in order to unveil a morphological and interpretable structure of the data. Additionally, we want this decomposition to be computed online for any new sample that is not part of the initial dataset. Therefore, our solution relies on a sparse, non-negative auto-encoder where the encoder is deep (for accuracy) and the decoder shallow (for interpretability). This method compares favorably to the state-of-the-art online methods on two datasets (MNIST and Fashion MNIST), according to classical metrics and to a new one we introduce, based on the invariance of the representation to morphological dilation.

Psychophysics, Gestalts and Games

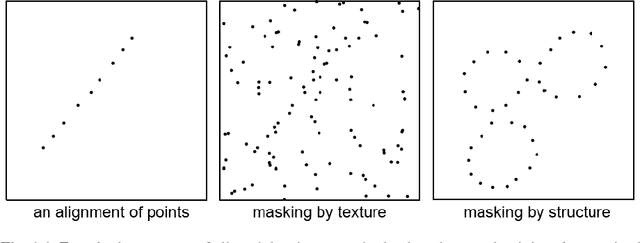
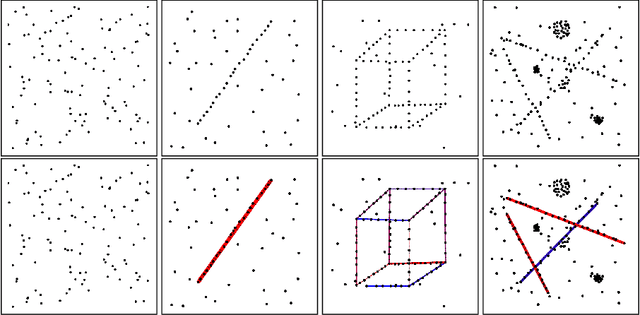
Many psychophysical studies are dedicated to the evaluation of the human gestalt detection on dot or Gabor patterns, and to model its dependence on the pattern and background parameters. Nevertheless, even for these constrained percepts, psychophysics have not yet reached the challenging prediction stage, where human detection would be quantitatively predicted by a (generic) model. On the other hand, Computer Vision has attempted at defining automatic detection thresholds. This chapter sketches a procedure to confront these two methodologies inspired in gestaltism. Using a computational quantitative version of the non-accidentalness principle, we raise the possibility that the psychophysical and the (older) gestaltist setups, both applicable on dot or Gabor patterns, find a useful complement in a Turing test. In our perceptual Turing test, human performance is compared by the scientist to the detection result given by a computer. This confrontation permits to revive the abandoned method of gestaltic games. We sketch the elaboration of such a game, where the subjects of the experiment are confronted to an alignment detection algorithm, and are invited to draw examples that will fool it. We show that in that way a more precise definition of the alignment gestalt and of its computational formulation seems to emerge. Detection algorithms might also be relevant to more classic psychophysical setups, where they can again play the role of a Turing test. To a visual experiment where subjects were invited to detect alignments in Gabor patterns, we associated a single function measuring the alignment detectability in the form of a number of false alarms (NFA). The first results indicate that the values of the NFA, as a function of all simulation parameters, are highly correlated to the human detection. This fact, that we intend to support by further experiments , might end up confirming that human alignment detection is the result of a single mechanism.