Moving Frame Net: SE-Equivariant Network for Volumes

Equivariance of neural networks to transformations helps to improve their performance and reduce generalization error in computer vision tasks, as they apply to datasets presenting symmetries (e.g. scalings, rotations, translations). The method of moving frames is classical for deriving operators invariant to the action of a Lie group in a manifold.Recently, a rotation and translation equivariant neural network for image data was proposed based on the moving frames approach. In this paper we significantly improve that approach by reducing the computation of moving frames to only one, at the input stage, instead of repeated computations at each layer. The equivariance of the resulting architecture is proved theoretically and we build a rotation and translation equivariant neural network to process volumes, i.e. signals on the 3D space. Our trained model overperforms the benchmarks in the medical volume classification of most of the tested datasets from MedMNIST3D.

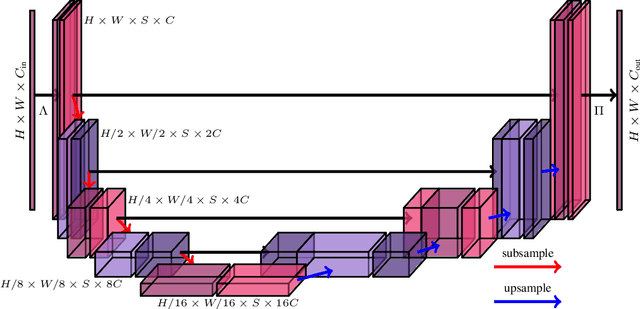
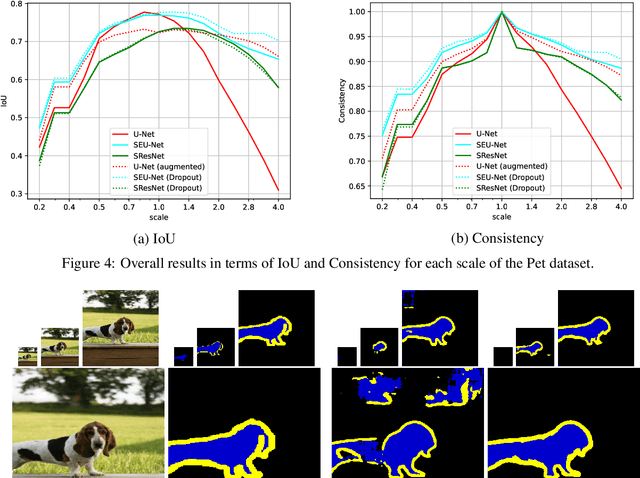
Scale Equivariant U-Net

In neural networks, the property of being equivariant to transformations improves generalization when the corresponding symmetry is present in the data. In particular, scale-equivariant networks are suited to computer vision tasks where the same classes of objects appear at different scales, like in most semantic segmentation tasks. Recently, convolutional layers equivariant to a semigroup of scalings and translations have been proposed. However, the equivariance of subsampling and upsampling has never been explicitly studied even though they are necessary building blocks in some segmentation architectures. The U-Net is a representative example of such architectures, which includes the basic elements used for state-of-the-art semantic segmentation. Therefore, this paper introduces the Scale Equivariant U-Net (SEU-Net), a U-Net that is made approximately equivariant to a semigroup of scales and translations through careful application of subsampling and upsampling layers and the use of aforementioned scale-equivariant layers. Moreover, a scale-dropout is proposed in order to improve generalization to different scales in approximately scale-equivariant architectures. The proposed SEU-Net is trained for semantic segmentation of the Oxford Pet IIIT and the DIC-C2DH-HeLa dataset for cell segmentation. The generalization metric to unseen scales is dramatically improved in comparison to the U-Net, even when the U-Net is trained with scale jittering, and to a scale-equivariant architecture that does not perform upsampling operators inside the equivariant pipeline. The scale-dropout induces better generalization on the scale-equivariant models in the Pet experiment, but not on the cell segmentation experiment.

Differential invariants for SE(2)-equivariant networks

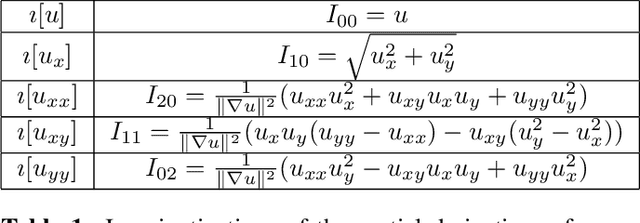
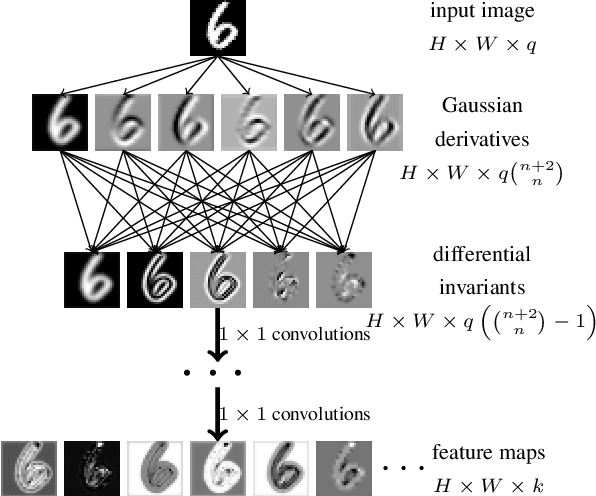
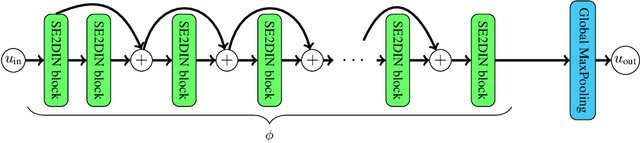
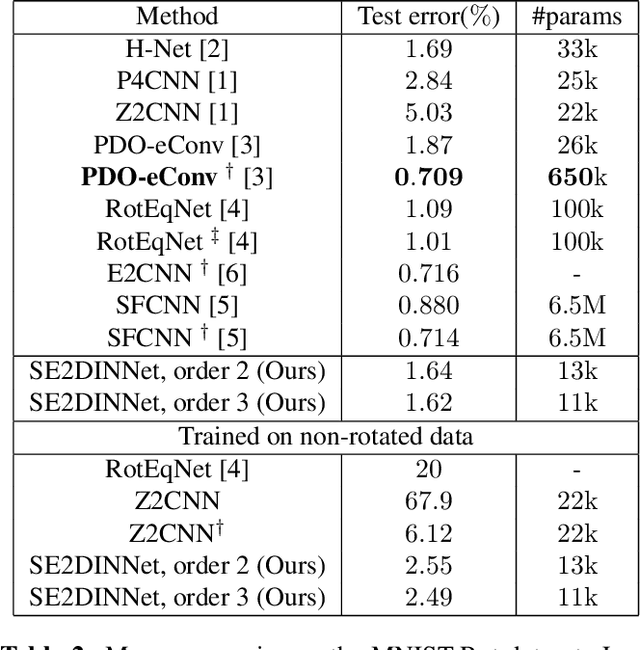
Symmetry is present in many tasks in computer vision, where the same class of objects can appear transformed, e.g. rotated due to different camera orientations, or scaled due to perspective. The knowledge of such symmetries in data coupled with equivariance of neural networks can improve their generalization to new samples. Differential invariants are equivariant operators computed from the partial derivatives of a function. In this paper we use differential invariants to define equivariant operators that form the layers of an equivariant neural network. Specifically, we derive invariants of the Special Euclidean Group SE(2), composed of rotations and translations, and apply them to construct a SE(2)-equivariant network, called SE(2) Differential Invariants Network (SE2DINNet). The network is subsequently tested in classification tasks which require a degree of equivariance or invariance to rotations. The results compare positively with the state-of-the-art, even though the proposed SE2DINNet has far less parameters than the compared models.

Scale Equivariant Neural Networks with Morphological Scale-Spaces

The translation equivariance of convolutions can make convolutional neural networks translation equivariant or invariant. Equivariance to other transformations (e.g. rotations, affine transformations, scalings) may also be desirable as soon as we know a priori that transformed versions of the same objects appear in the data. The semigroup cross-correlation, which is a linear operator equivariant to semigroup actions, was recently proposed and applied in conjunction with the Gaussian scale-space to create architectures which are equivariant to discrete scalings. In this paper, a generalization using a broad class of liftings, including morphological scale-spaces, is proposed. The architectures obtained from different scale-spaces are tested and compared in supervised classification and semantic segmentation tasks where objects in test images appear at different scales compared to training images. In both classification and segmentation tasks, the scale-equivariant architectures improve dramatically the generalization to unseen scales compared to a convolutional baseline. Besides, in our experiments morphological scale-spaces outperformed the Gaussian scale-space in geometrical tasks.