MorphoActivation: Generalizing ReLU activation function by mathematical morphology

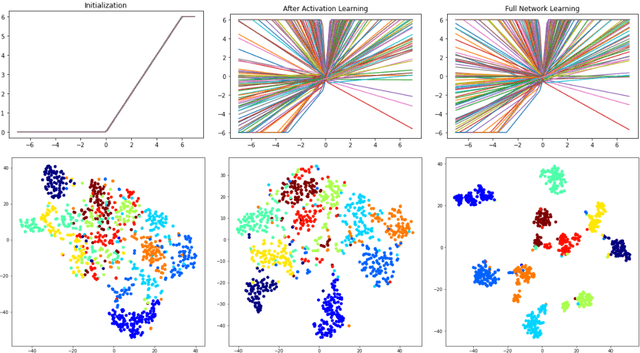
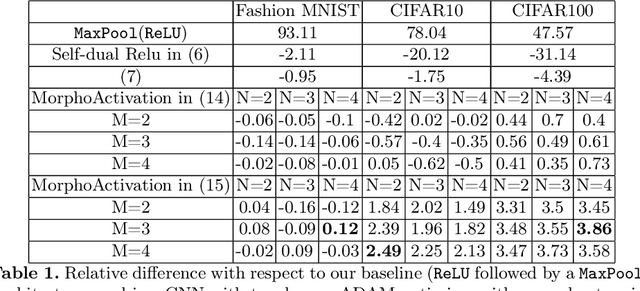
This paper analyses both nonlinear activation functions and spatial max-pooling for Deep Convolutional Neural Networks (DCNNs) by means of the algebraic basis of mathematical morphology. Additionally, a general family of activation functions is proposed by considering both max-pooling and nonlinear operators in the context of morphological representations. Experimental section validates the goodness of our approach on classical benchmarks for supervised learning by DCNN.

Differential invariants for SE(2)-equivariant networks

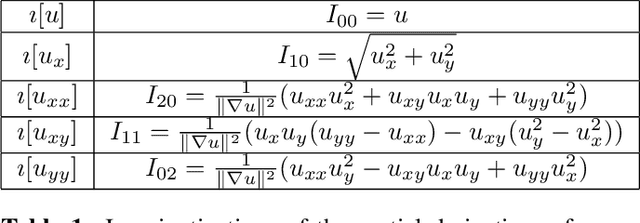
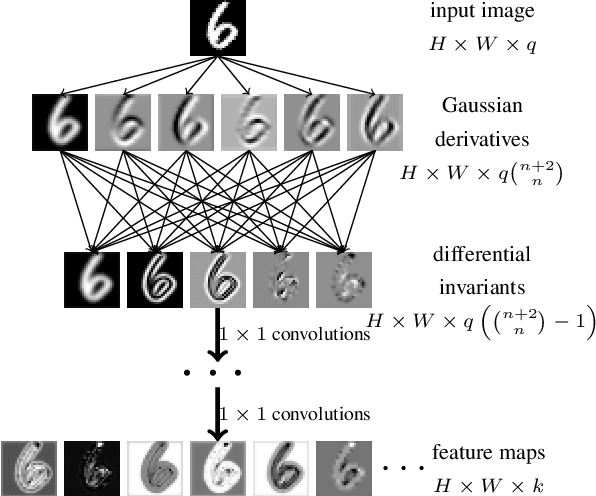
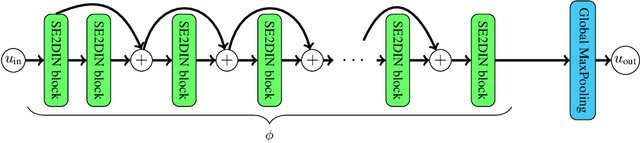
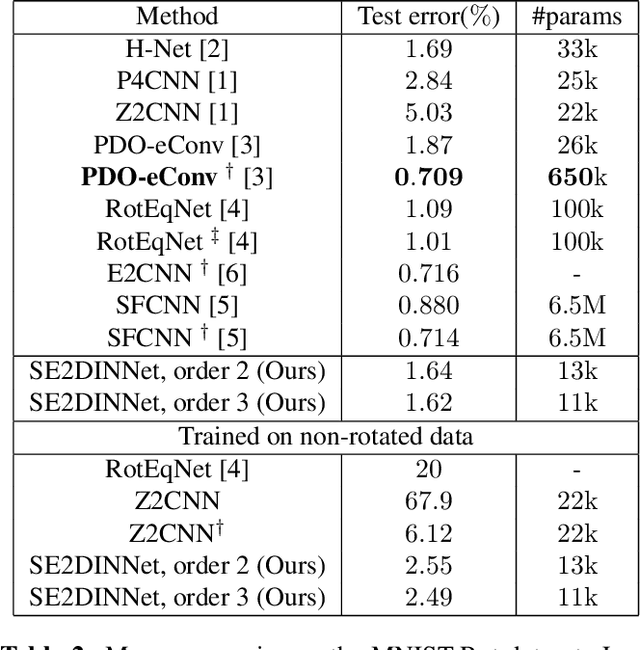
Symmetry is present in many tasks in computer vision, where the same class of objects can appear transformed, e.g. rotated due to different camera orientations, or scaled due to perspective. The knowledge of such symmetries in data coupled with equivariance of neural networks can improve their generalization to new samples. Differential invariants are equivariant operators computed from the partial derivatives of a function. In this paper we use differential invariants to define equivariant operators that form the layers of an equivariant neural network. Specifically, we derive invariants of the Special Euclidean Group SE(2), composed of rotations and translations, and apply them to construct a SE(2)-equivariant network, called SE(2) Differential Invariants Network (SE2DINNet). The network is subsequently tested in classification tasks which require a degree of equivariance or invariance to rotations. The results compare positively with the state-of-the-art, even though the proposed SE2DINNet has far less parameters than the compared models.

A Learning Framework for Morphological Operators using Counter-Harmonic Mean

We present a novel framework for learning morphological operators using counter-harmonic mean. It combines concepts from morphology and convolutional neural networks. A thorough experimental validation analyzes basic morphological operators dilation and erosion, opening and closing, as well as the much more complex top-hat transform, for which we report a real-world application from the steel industry. Using online learning and stochastic gradient descent, our system learns both the structuring element and the composition of operators. It scales well to large datasets and online settings.