Simulation of microstructures and machine learning

Machine learning offers attractive solutions to challenging image processing tasks. Tedious development and parametrization of algorithmic solutions can be replaced by training a convolutional neural network or a random forest with a high potential to generalize. However, machine learning methods rely on huge amounts of representative image data along with a ground truth, usually obtained by manual annotation. Thus, limited availability of training data is a critical bottleneck. We discuss two use cases: optical quality control in industrial production and segmenting crack structures in 3D images of concrete. For optical quality control, all defect types have to be trained but are typically not evenly represented in the training data. Additionally, manual annotation is costly and often inconsistent. It is nearly impossible in the second case: segmentation of crack systems in 3D images of concrete. Synthetic images, generated based on realizations of stochastic geometry models, offer an elegant way out. A wide variety of structure types can be generated. The within structure variation is naturally captured by the stochastic nature of the models and the ground truth is for free. Many new questions arise. In particular, which characteristics of the real image data have to be met to which degree of fidelity.

Cracks in concrete

Finding and properly segmenting cracks in images of concrete is a challenging task. Cracks are thin and rough and being air filled do yield a very weak contrast in 3D images obtained by computed tomography. Enhancing and segmenting dark lower-dimensional structures is already demanding. The heterogeneous concrete matrix and the size of the images further increase the complexity. ML methods have proven to solve difficult segmentation problems when trained on enough and well annotated data. However, so far, there is not much 3D image data of cracks available at all, let alone annotated. Interactive annotation is error-prone as humans can easily tell cats from dogs or roads without from roads with cars but have a hard time deciding whether a thin and dark structure seen in a 2D slice continues in the next one. Training networks by synthetic, simulated images is an elegant way out, bears however its own challenges. In this contribution, we describe how to generate semi-synthetic image data to train CNN like the well known 3D U-Net or random forests for segmenting cracks in 3D images of concrete. The thickness of real cracks varies widely, both, within one crack as well as from crack to crack in the same sample. The segmentation method should therefore be invariant with respect to scale changes. We introduce the so-called RieszNet, designed for exactly this purpose. Finally, we discuss how to generalize the ML crack segmentation methods to other concrete types.

Towards Generalized Entropic Sparsification for Convolutional Neural Networks

Convolutional neural networks (CNNs) are reported to be overparametrized. The search for optimal (minimal) and sufficient architecture is an NP-hard problem as the hyperparameter space for possible network configurations is vast. Here, we introduce a layer-by-layer data-driven pruning method based on the mathematical idea aiming at a computationally-scalable entropic relaxation of the pruning problem. The sparse subnetwork is found from the pre-trained (full) CNN using the network entropy minimization as a sparsity constraint. This allows deploying a numerically scalable algorithm with a sublinear scaling cost. The method is validated on several benchmarks (architectures): (i) MNIST (LeNet) with sparsity 55%-84% and loss in accuracy 0.1%-0.5%, and (ii) CIFAR-10 (VGG-16, ResNet18) with sparsity 73-89% and loss in accuracy 0.1%-0.5%.

Riesz feature representation: scale equivariant scattering network for classification tasks

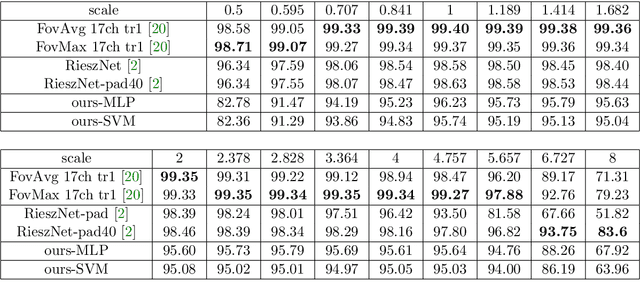
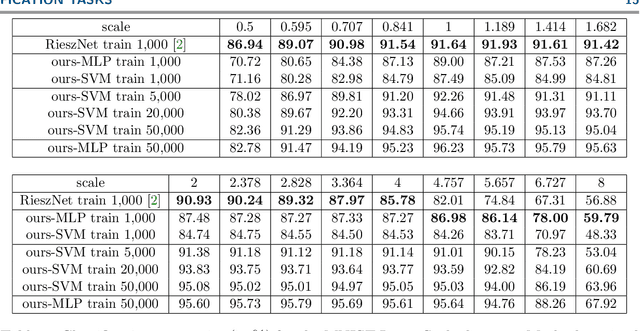
Scattering networks yield powerful and robust hierarchical image descriptors which do not require lengthy training and which work well with very few training data. However, they rely on sampling the scale dimension. Hence, they become sensitive to scale variations and are unable to generalize to unseen scales. In this work, we define an alternative feature representation based on the Riesz transform. We detail and analyze the mathematical foundations behind this representation. In particular, it inherits scale equivariance from the Riesz transform and completely avoids sampling of the scale dimension. Additionally, the number of features in the representation is reduced by a factor four compared to scattering networks. Nevertheless, our representation performs comparably well for texture classification with an interesting addition: scale equivariance. Our method yields superior performance when dealing with scales outside of those covered by the training dataset. The usefulness of the equivariance property is demonstrated on the digit classification task, where accuracy remains stable even for scales four times larger than the one chosen for training. As a second example, we consider classification of textures.

Riesz networks: scale invariant neural networks in a single forward pass

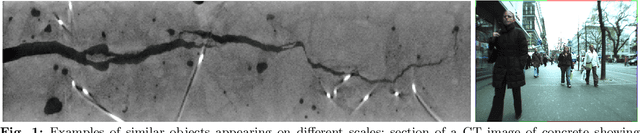
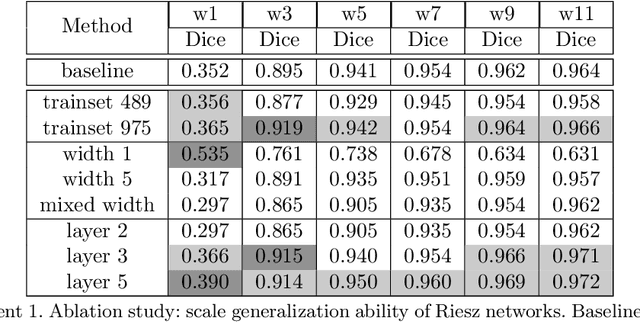
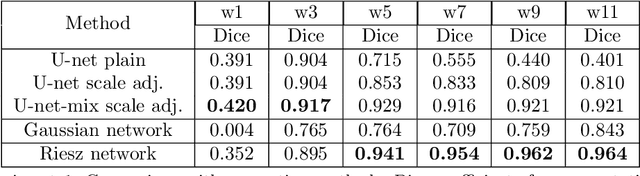
Scale invariance of an algorithm refers to its ability to treat objects equally independently of their size. For neural networks, scale invariance is typically achieved by data augmentation. However, when presented with a scale far outside the range covered by the training set, neural networks may fail to generalize. Here, we introduce the Riesz network, a novel scale invariant neural network. Instead of standard 2d or 3d convolutions for combining spatial information, the Riesz network is based on the Riesz transform which is a scale equivariant operation. As a consequence, this network naturally generalizes to unseen or even arbitrary scales in a single forward pass. As an application example, we consider detecting and segmenting cracks in tomographic images of concrete. In this context, 'scale' refers to the crack thickness which may vary strongly even within the same sample. To prove its scale invariance, the Riesz network is trained on one fixed crack width. We then validate its performance in segmenting simulated and real tomographic images featuring a wide range of crack widths. An additional experiment is carried out on the MNIST Large Scale data set.

Methods for segmenting cracks in 3d images of concrete: A comparison based on semi-synthetic images

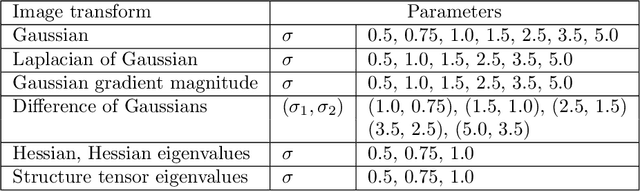
Concrete is the standard construction material for buildings, bridges, and roads. As safety plays a central role in the design, monitoring, and maintenance of such constructions, it is important to understand the cracking behavior of concrete. Computed tomography captures the microstructure of building materials and allows to study crack initiation and propagation. Manual segmentation of crack surfaces in large 3d images is not feasible. In this paper, automatic crack segmentation methods for 3d images are reviewed and compared. Classical image processing methods (edge detection filters, template matching, minimal path and region growing algorithms) and learning methods (convolutional neural networks, random forests) are considered and tested on semi-synthetic 3d images. Their performance strongly depends on parameter selection which should be adapted to the grayvalue distribution of the images and the geometric properties of the concrete. In general, the learning methods perform best, in particular for thin cracks and low grayvalue contrast.