Hilbert curves for efficient exploratory landscape analysis neighbourhood sampling

Landscape analysis aims to characterise optimisation problems based on their objective (or fitness) function landscape properties. The problem search space is typically sampled, and various landscape features are estimated based on the samples. One particularly salient set of features is information content, which requires the samples to be sequences of neighbouring solutions, such that the local relationships between consecutive sample points are preserved. Generating such spatially correlated samples that also provide good search space coverage is challenging. It is therefore common to first obtain an unordered sample with good search space coverage, and then apply an ordering algorithm such as the nearest neighbour to minimise the distance between consecutive points in the sample. However, the nearest neighbour algorithm becomes computationally prohibitive in higher dimensions, thus there is a need for more efficient alternatives. In this study, Hilbert space-filling curves are proposed as a method to efficiently obtain high-quality ordered samples. Hilbert curves are a special case of fractal curves, and guarantee uniform coverage of a bounded search space while providing a spatially correlated sample. We study the effectiveness of Hilbert curves as samplers, and discover that they are capable of extracting salient features at a fraction of the computational cost compared to Latin hypercube sampling with post-factum ordering. Further, we investigate the use of Hilbert curves as an ordering strategy, and find that they order the sample significantly faster than the nearest neighbour ordering, without sacrificing the saliency of the extracted features.

Hybridised Loss Functions for Improved Neural Network Generalisation

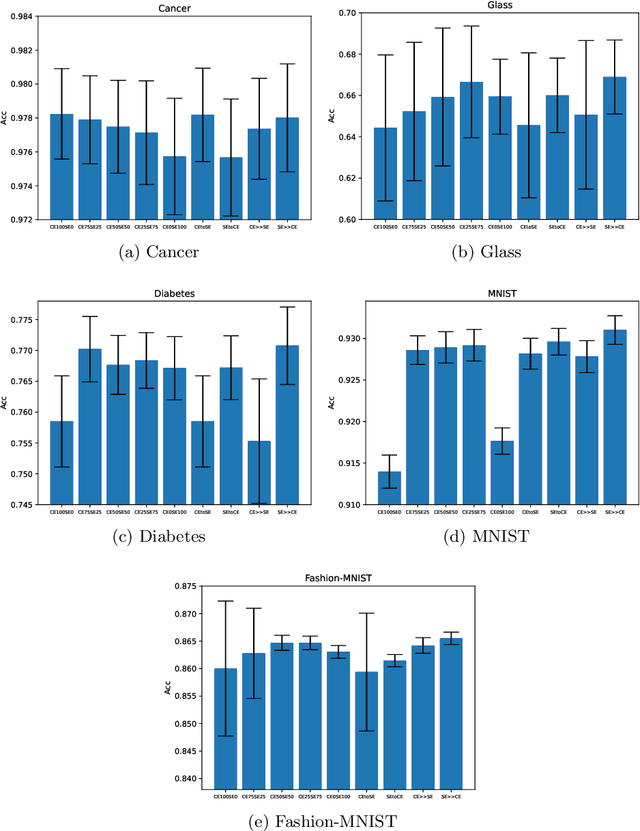
Loss functions play an important role in the training of artificial neural networks (ANNs), and can affect the generalisation ability of the ANN model, among other properties. Specifically, it has been shown that the cross entropy and sum squared error loss functions result in different training dynamics, and exhibit different properties that are complementary to one another. It has previously been suggested that a hybrid of the entropy and sum squared error loss functions could combine the advantages of the two functions, while limiting their disadvantages. The effectiveness of such hybrid loss functions is investigated in this study. It is shown that hybridisation of the two loss functions improves the generalisation ability of the ANNs on all problems considered. The hybrid loss function that starts training with the sum squared error loss function and later switches to the cross entropy error loss function is shown to either perform the best on average, or to not be significantly different than the best loss function tested for all problems considered. This study shows that the minima discovered by the sum squared error loss function can be further exploited by switching to cross entropy error loss function. It can thus be concluded that hybridisation of the two loss functions could lead to better performance in ANNs.

A Scalable Continuous Unbounded Optimisation Benchmark Suite from Neural Network Regression

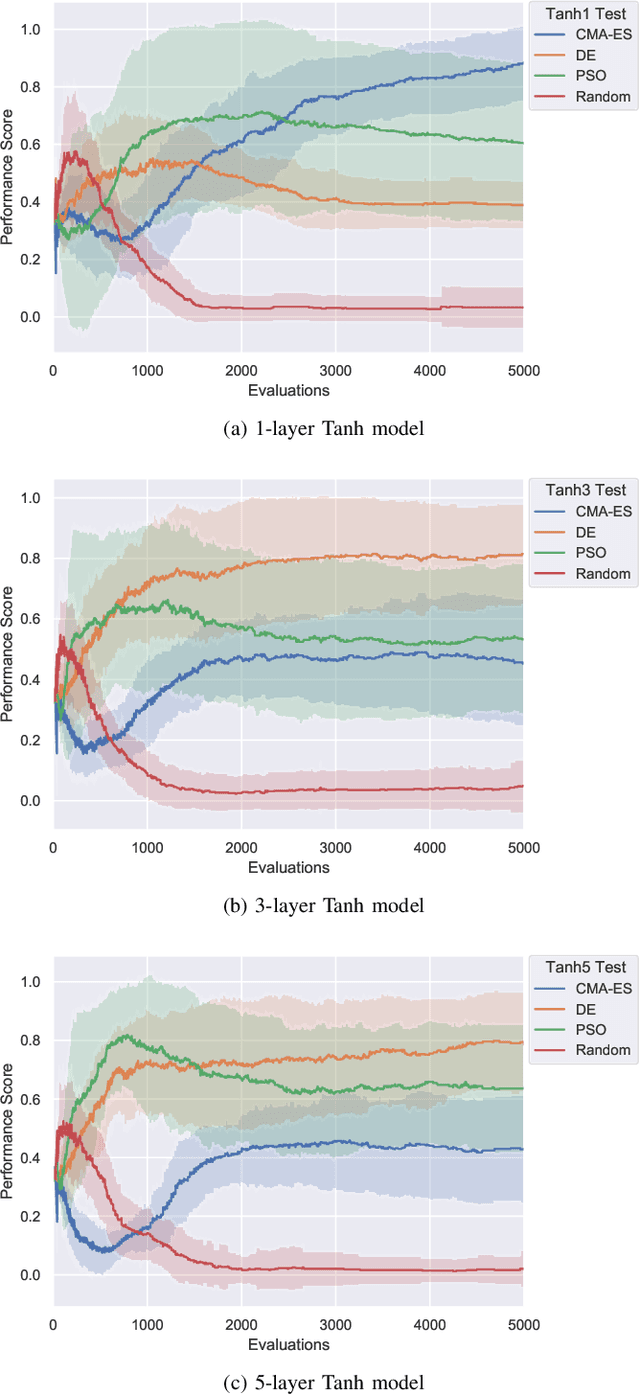
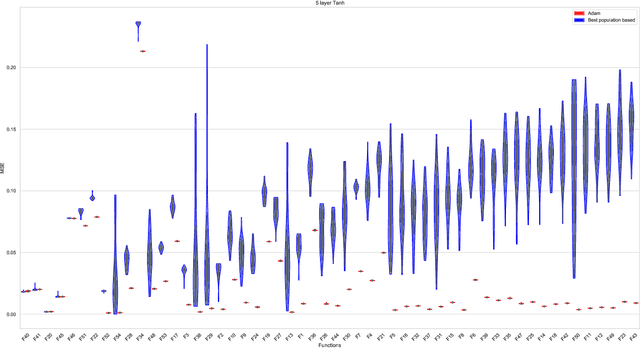
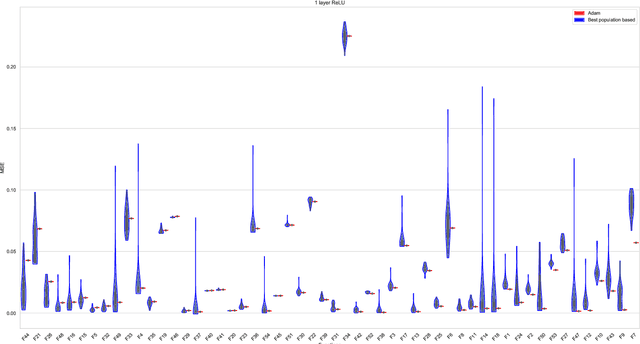
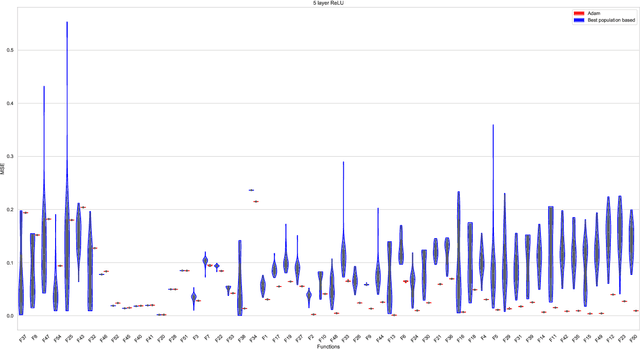
For the design of optimisation algorithms that perform well in general, it is necessary to experiment with and benchmark on a range of problems with diverse characteristics. The training of neural networks is an optimisation task that has gained prominence with the recent successes of deep learning. Although evolutionary algorithms have been used for training neural networks, gradient descent variants are by far the most common choice with their trusted good performance on large-scale machine learning tasks. With this paper we contribute CORNN (Continuous Optimisation of Regression tasks using Neural Networks), a large suite that can easily be used to benchmark the performance of any continuous black-box algorithm on neural network training problems. By employing different base regression functions and neural network architectures, problem instances with different dimensions and levels of difficulty can be created. We demonstrate the use of the CORNN Suite by comparing the performance of three evolutionary and swarm-based algorithms on a set of over 300 problem instances. With the exception of random search, we provide evidence of performance complementarity between the algorithms. As a baseline, results are also provided to contrast the performance of the best population-based algorithm against a gradient-based approach (Adam). The suite is shared as a public web repository to facilitate easy integration with existing benchmarking platforms.

A survey of benchmarking frameworks for reinforcement learning

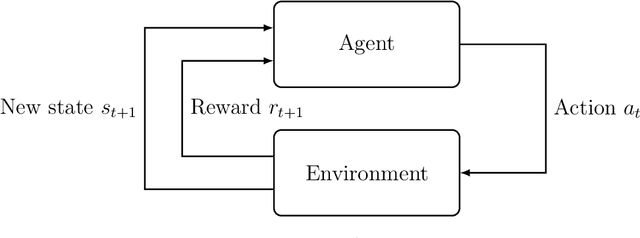
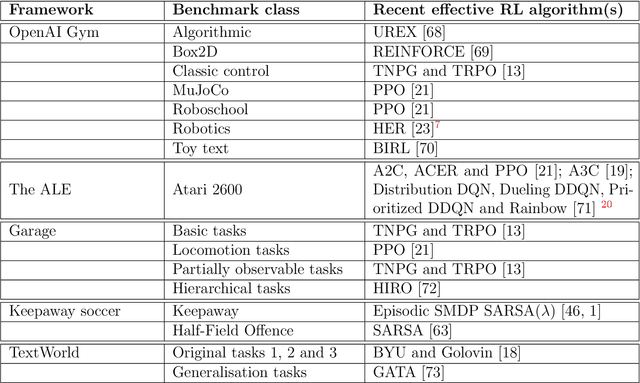
Reinforcement learning has recently experienced increased prominence in the machine learning community. There are many approaches to solving reinforcement learning problems with new techniques developed constantly. When solving problems using reinforcement learning, there are various difficult challenges to overcome. To ensure progress in the field, benchmarks are important for testing new algorithms and comparing with other approaches. The reproducibility of results for fair comparison is therefore vital in ensuring that improvements are accurately judged. This paper provides an overview of different contributions to reinforcement learning benchmarking and discusses how they can assist researchers to address the challenges facing reinforcement learning. The contributions discussed are the most used and recent in the literature. The paper discusses the contributions in terms of implementation, tasks and provided algorithm implementations with benchmarks. The survey aims to bring attention to the wide range of reinforcement learning benchmarking tasks available and to encourage research to take place in a standardised manner. Additionally, this survey acts as an overview for researchers not familiar with the different tasks that can be used to develop and test new reinforcement learning algorithms.

Benchmarking in Optimization: Best Practice and Open Issues

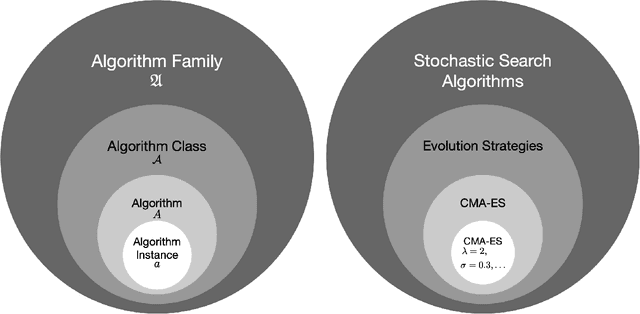
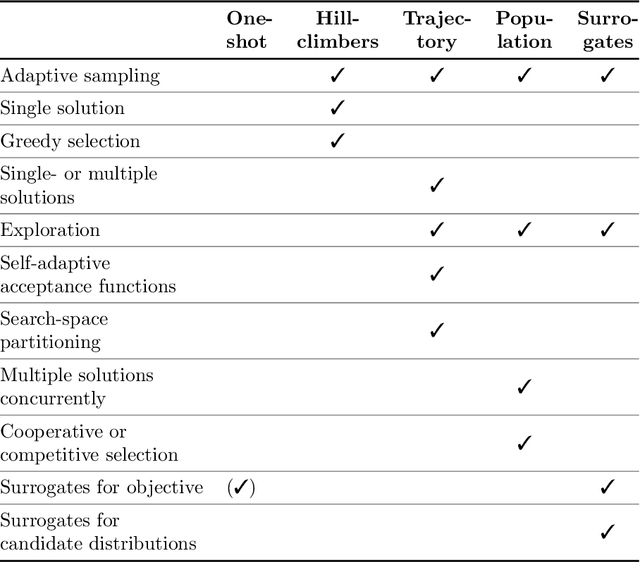
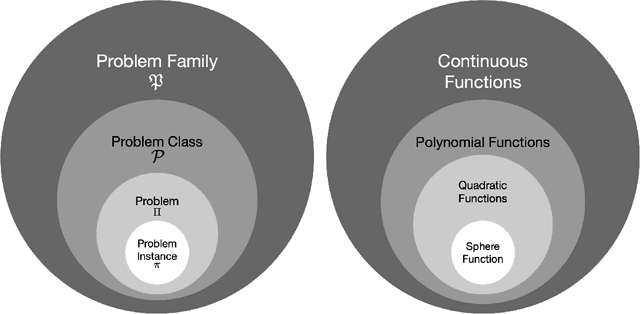
This survey compiles ideas and recommendations from more than a dozen researchers with different backgrounds and from different institutes around the world. Promoting best practice in benchmarking is its main goal. The article discusses eight essential topics in benchmarking: clearly stated goals, well-specified problems, suitable algorithms, adequate performance measures, thoughtful analysis, effective and efficient designs, comprehensible presentations, and guaranteed reproducibility. The final goal is to provide well-accepted guidelines (rules) that might be useful for authors and reviewers. As benchmarking in optimization is an active and evolving field of research this manuscript is meant to co-evolve over time by means of periodic updates.