Belinda Stapelberg
A survey of benchmarking frameworks for reinforcement learning
Nov 27, 2020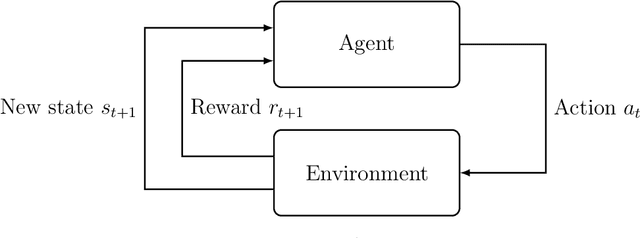
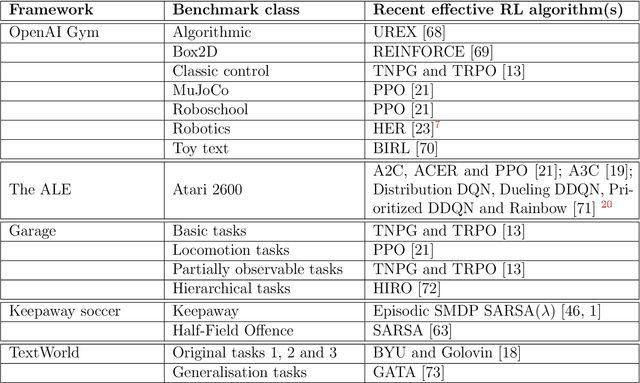
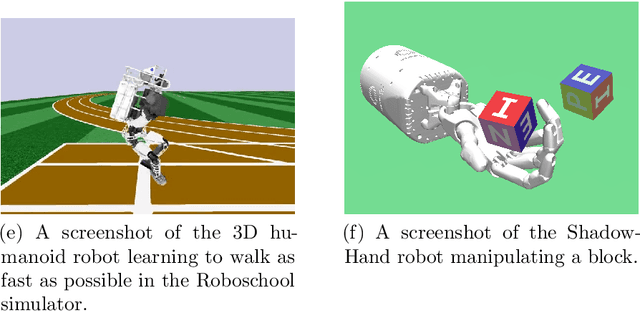
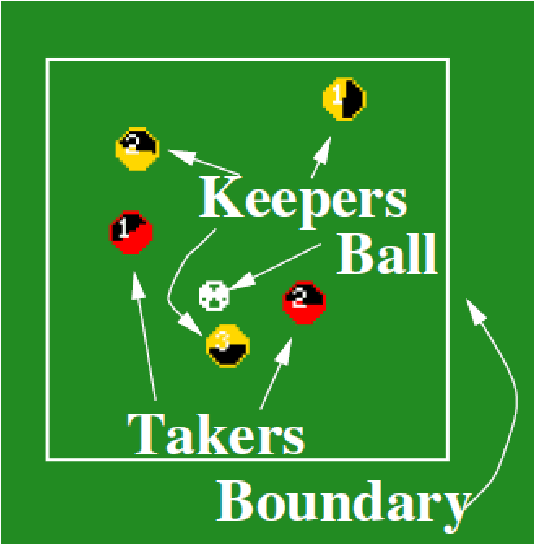
Abstract:Reinforcement learning has recently experienced increased prominence in the machine learning community. There are many approaches to solving reinforcement learning problems with new techniques developed constantly. When solving problems using reinforcement learning, there are various difficult challenges to overcome. To ensure progress in the field, benchmarks are important for testing new algorithms and comparing with other approaches. The reproducibility of results for fair comparison is therefore vital in ensuring that improvements are accurately judged. This paper provides an overview of different contributions to reinforcement learning benchmarking and discusses how they can assist researchers to address the challenges facing reinforcement learning. The contributions discussed are the most used and recent in the literature. The paper discusses the contributions in terms of implementation, tasks and provided algorithm implementations with benchmarks. The survey aims to bring attention to the wide range of reinforcement learning benchmarking tasks available and to encourage research to take place in a standardised manner. Additionally, this survey acts as an overview for researchers not familiar with the different tasks that can be used to develop and test new reinforcement learning algorithms.
Particle Swarm Optimization: Stability Analysis using N-Informers under Arbitrary Coefficient Distributions
Apr 01, 2020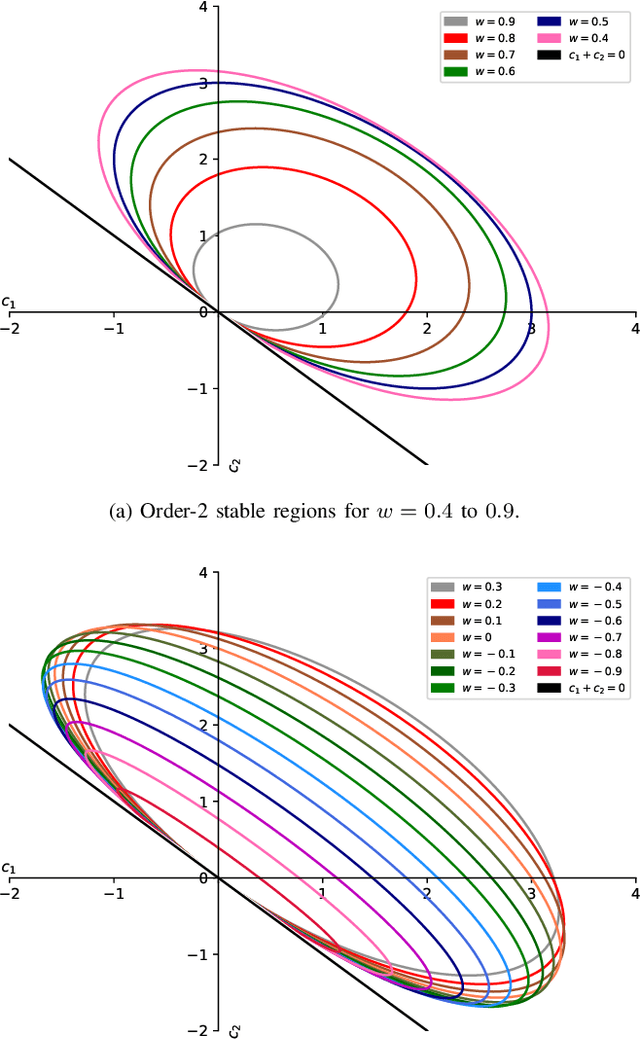
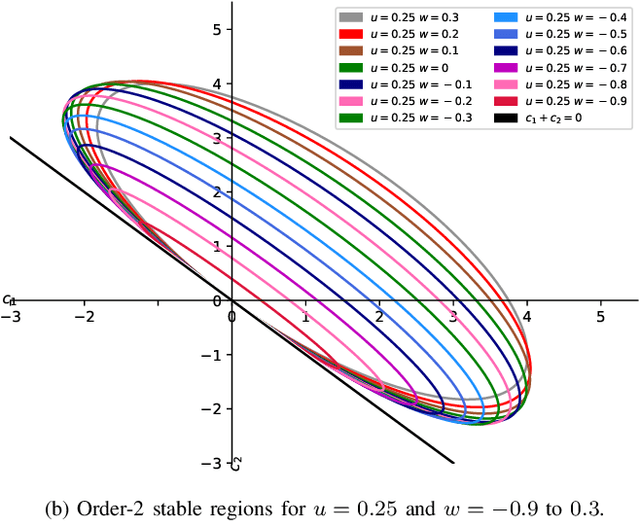
Abstract:This paper derives, under minimal modelling assumptions, a simple to use theorem for obtaining both order-$1$ and order-$2$ stability criteria for a common class of particle swarm optimization (PSO) variants. Specifically, PSO variants that can be rewritten as a finite sum of stochastically weighted difference vectors between a particle's position and swarm informers are covered by the theorem. Additionally, the use of the derived theorem allows a PSO practitioner to obtain stability criteria that contains no artificial restriction on the relationship between control coefficients. Almost all previous PSO stability results have provided stability criteria under the restriction that the social and cognitive control coefficients are equal; such restrictions are not present when using the derived theorem. Using the derived theorem, as demonstration of its ease of use, stability criteria are derived without the imposed restriction on the relation between the control coefficients for three popular PSO variants.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge