Particle Swarm Optimization: Stability Analysis using N-Informers under Arbitrary Coefficient Distributions
Paper and Code
Apr 01, 2020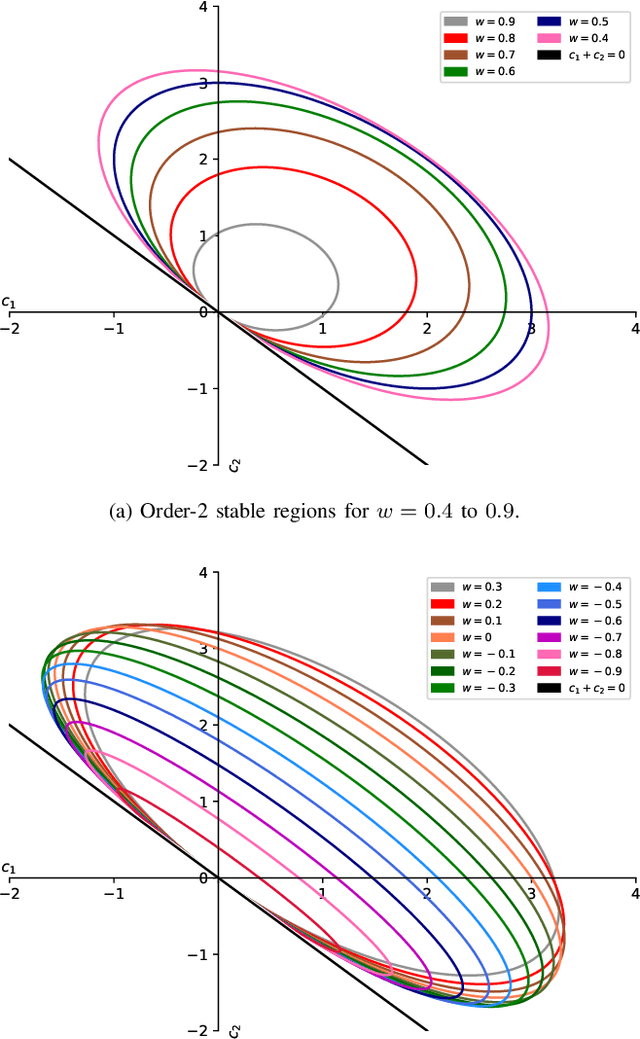
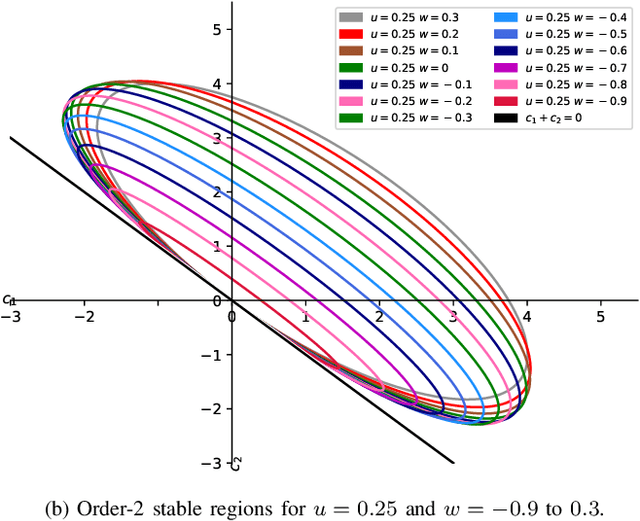
This paper derives, under minimal modelling assumptions, a simple to use theorem for obtaining both order-$1$ and order-$2$ stability criteria for a common class of particle swarm optimization (PSO) variants. Specifically, PSO variants that can be rewritten as a finite sum of stochastically weighted difference vectors between a particle's position and swarm informers are covered by the theorem. Additionally, the use of the derived theorem allows a PSO practitioner to obtain stability criteria that contains no artificial restriction on the relationship between control coefficients. Almost all previous PSO stability results have provided stability criteria under the restriction that the social and cognitive control coefficients are equal; such restrictions are not present when using the derived theorem. Using the derived theorem, as demonstration of its ease of use, stability criteria are derived without the imposed restriction on the relation between the control coefficients for three popular PSO variants.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge