Hilbert curves for efficient exploratory landscape analysis neighbourhood sampling

Landscape analysis aims to characterise optimisation problems based on their objective (or fitness) function landscape properties. The problem search space is typically sampled, and various landscape features are estimated based on the samples. One particularly salient set of features is information content, which requires the samples to be sequences of neighbouring solutions, such that the local relationships between consecutive sample points are preserved. Generating such spatially correlated samples that also provide good search space coverage is challenging. It is therefore common to first obtain an unordered sample with good search space coverage, and then apply an ordering algorithm such as the nearest neighbour to minimise the distance between consecutive points in the sample. However, the nearest neighbour algorithm becomes computationally prohibitive in higher dimensions, thus there is a need for more efficient alternatives. In this study, Hilbert space-filling curves are proposed as a method to efficiently obtain high-quality ordered samples. Hilbert curves are a special case of fractal curves, and guarantee uniform coverage of a bounded search space while providing a spatially correlated sample. We study the effectiveness of Hilbert curves as samplers, and discover that they are capable of extracting salient features at a fraction of the computational cost compared to Latin hypercube sampling with post-factum ordering. Further, we investigate the use of Hilbert curves as an ordering strategy, and find that they order the sample significantly faster than the nearest neighbour ordering, without sacrificing the saliency of the extracted features.

Denoising Diffusion Post-Processing for Low-Light Image Enhancement

Low-light image enhancement (LLIE) techniques attempt to increase the visibility of images captured in low-light scenarios. However, as a result of enhancement, a variety of image degradations such as noise and color bias are revealed. Furthermore, each particular LLIE approach may introduce a different form of flaw within its enhanced results. To combat these image degradations, post-processing denoisers have widely been used, which often yield oversmoothed results lacking detail. We propose using a diffusion model as a post-processing approach, and we introduce Low-light Post-processing Diffusion Model (LPDM) in order to model the conditional distribution between under-exposed and normally-exposed images. We apply LPDM in a manner which avoids the computationally expensive generative reverse process of typical diffusion models, and post-process images in one pass through LPDM. Extensive experiments demonstrate that our approach outperforms competing post-processing denoisers by increasing the perceptual quality of enhanced low-light images on a variety of challenging low-light datasets. Source code is available at https://github.com/savvaki/LPDM.

Hybridised Loss Functions for Improved Neural Network Generalisation

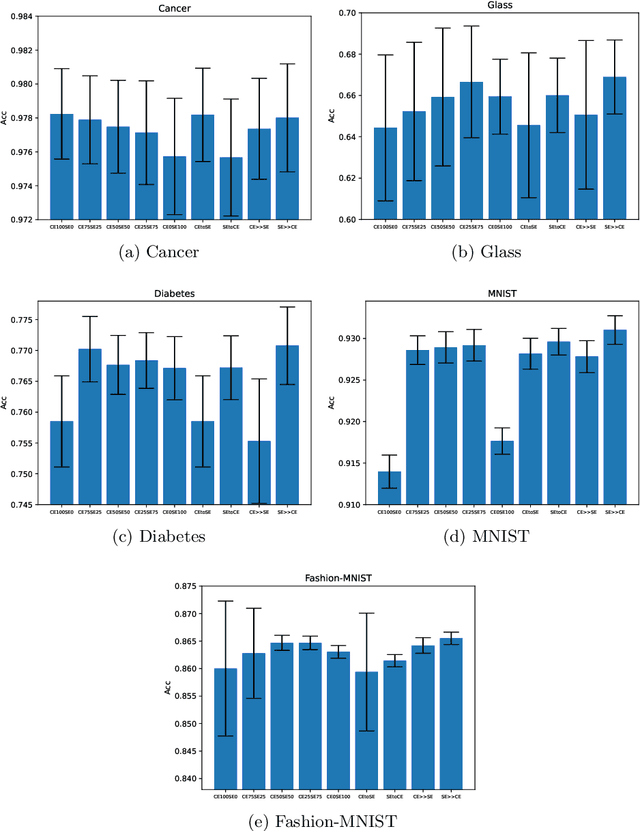
Loss functions play an important role in the training of artificial neural networks (ANNs), and can affect the generalisation ability of the ANN model, among other properties. Specifically, it has been shown that the cross entropy and sum squared error loss functions result in different training dynamics, and exhibit different properties that are complementary to one another. It has previously been suggested that a hybrid of the entropy and sum squared error loss functions could combine the advantages of the two functions, while limiting their disadvantages. The effectiveness of such hybrid loss functions is investigated in this study. It is shown that hybridisation of the two loss functions improves the generalisation ability of the ANNs on all problems considered. The hybrid loss function that starts training with the sum squared error loss function and later switches to the cross entropy error loss function is shown to either perform the best on average, or to not be significantly different than the best loss function tested for all problems considered. This study shows that the minima discovered by the sum squared error loss function can be further exploited by switching to cross entropy error loss function. It can thus be concluded that hybridisation of the two loss functions could lead to better performance in ANNs.