Hybridised Loss Functions for Improved Neural Network Generalisation
Paper and Code
Apr 26, 2022
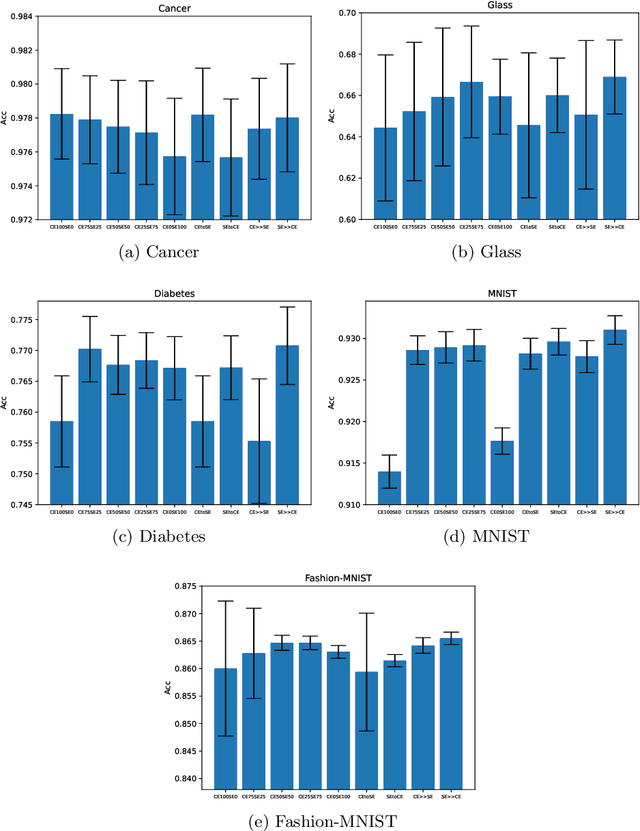


Loss functions play an important role in the training of artificial neural networks (ANNs), and can affect the generalisation ability of the ANN model, among other properties. Specifically, it has been shown that the cross entropy and sum squared error loss functions result in different training dynamics, and exhibit different properties that are complementary to one another. It has previously been suggested that a hybrid of the entropy and sum squared error loss functions could combine the advantages of the two functions, while limiting their disadvantages. The effectiveness of such hybrid loss functions is investigated in this study. It is shown that hybridisation of the two loss functions improves the generalisation ability of the ANNs on all problems considered. The hybrid loss function that starts training with the sum squared error loss function and later switches to the cross entropy error loss function is shown to either perform the best on average, or to not be significantly different than the best loss function tested for all problems considered. This study shows that the minima discovered by the sum squared error loss function can be further exploited by switching to cross entropy error loss function. It can thus be concluded that hybridisation of the two loss functions could lead to better performance in ANNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge