Learn Dynamic-Aware State Embedding for Transfer Learning

Transfer reinforcement learning aims to improve the sample efficiency of solving unseen new tasks by leveraging experiences obtained from previous tasks. We consider the setting where all tasks (MDPs) share the same environment dynamic except reward function. In this setting, the MDP dynamic is a good knowledge to transfer, which can be inferred by uniformly random policy. However, trajectories generated by uniform random policy are not useful for policy improvement, which impairs the sample efficiency severely. Instead, we observe that the binary MDP dynamic can be inferred from trajectories of any policy which avoids the need of uniform random policy. As the binary MDP dynamic contains the state structure shared over all tasks we believe it is suitable to transfer. Built on this observation, we introduce a method to infer the binary MDP dynamic on-line and at the same time utilize it to guide state embedding learning, which is then transferred to new tasks. We keep state embedding learning and policy learning separately. As a result, the learned state embedding is task and policy agnostic which makes it ideal for transfer learning. In addition, to facilitate the exploration over the state space, we propose a novel intrinsic reward based on the inferred binary MDP dynamic. Our method can be used out-of-box in combination with model-free RL algorithms. We show two instances on the basis of \algo{DQN} and \algo{A2C}. Empirical results of intensive experiments show the advantage of our proposed method in various transfer learning tasks.

Differentiable Linear Bandit Algorithm

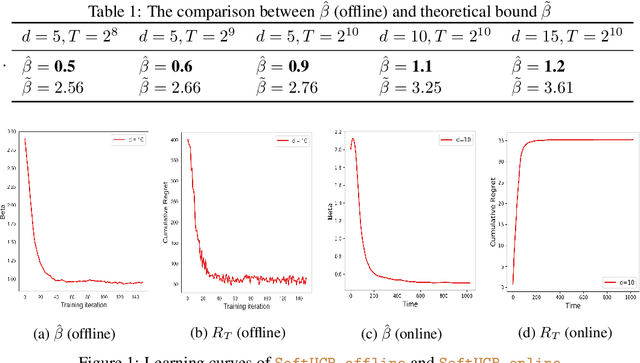
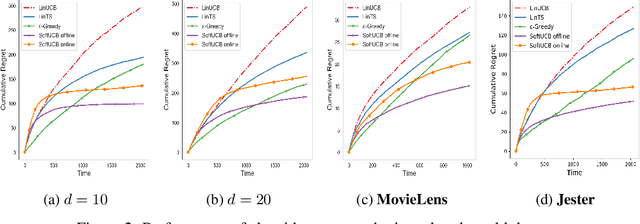
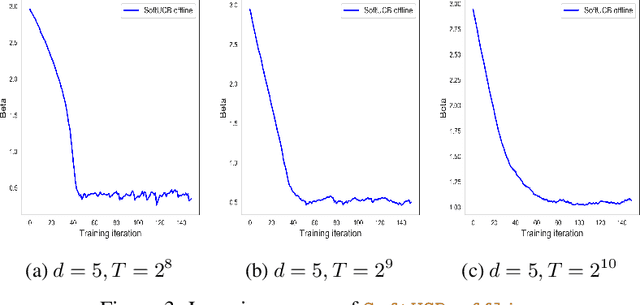
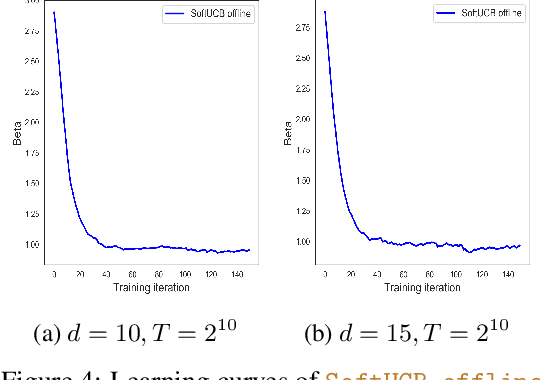
Upper Confidence Bound (UCB) is arguably the most commonly used method for linear multi-arm bandit problems. While conceptually and computationally simple, this method highly relies on the confidence bounds, failing to strike the optimal exploration-exploitation if these bounds are not properly set. In the literature, confidence bounds are typically derived from concentration inequalities based on assumptions on the reward distribution, e.g., sub-Gaussianity. The validity of these assumptions however is unknown in practice. In this work, we aim at learning the confidence bound in a data-driven fashion, making it adaptive to the actual problem structure. Specifically, noting that existing UCB-typed algorithms are not differentiable with respect to confidence bound, we first propose a novel differentiable linear bandit algorithm. Then, we introduce a gradient estimator, which allows the confidence bound to be learned via gradient ascent. Theoretically, we show that the proposed algorithm achieves a $\tilde{\mathcal{O}}(\hat{\beta}\sqrt{dT})$ upper bound of $T$-round regret, where $d$ is the dimension of arm features and $\hat{\beta}$ is the learned size of confidence bound. Empirical results show that $\hat{\beta}$ is significantly smaller than its theoretical upper bound and proposed algorithms outperforms baseline ones on both simulated and real-world datasets.

Laplacian-regularized graph bandits: Algorithms and theoretical analysis

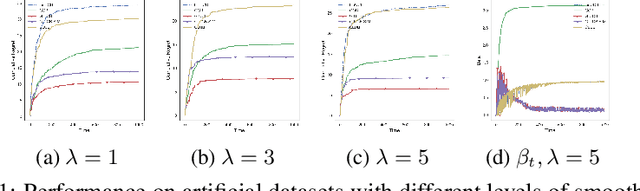
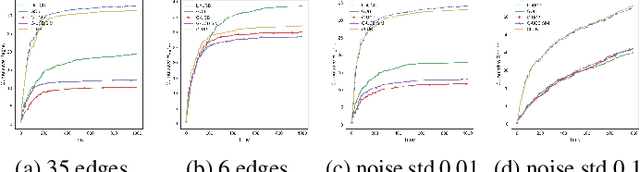
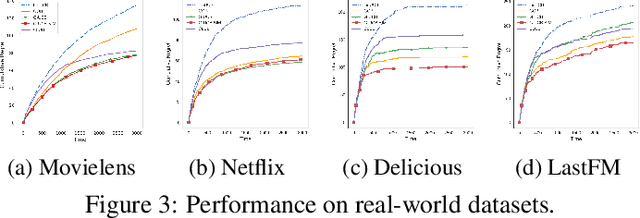
We study contextual multi-armed bandit problems in the case of multiple users, where we exploit the structure in the user domain to reduce the cumulative regret. Specifically, we model user relation as a graph, and assume that the parameters (preferences) of users form smooth signals on the graph. This leads to a graph Laplacian-regularized estimator, for which we propose a novel bandit algorithm whose performance depends on a notion of local smoothness on the graph. We provide a closed-form solution to the estimator, enabling a theoretical analysis on the convergence property of the estimator as well as single-user upper confidence bound (UCB) and cumulative regret of the proposed bandit algorithm. Furthermore, we show that the regret scales linearly with the local smoothness measure, which approaches zero for densely connected graph. The single-user UCB also allows us to further propose an extension of the bandit algorithm, whose computational complexity scales linearly with the number of users. We support theoretical claims with empirical evidences, and demonstrate the advantage of the proposed algorithm in comparison with state-of-the-art graph-based bandit algorithms on both synthetic and real-world datasets.

Error Analysis on Graph Laplacian Regularized Estimator

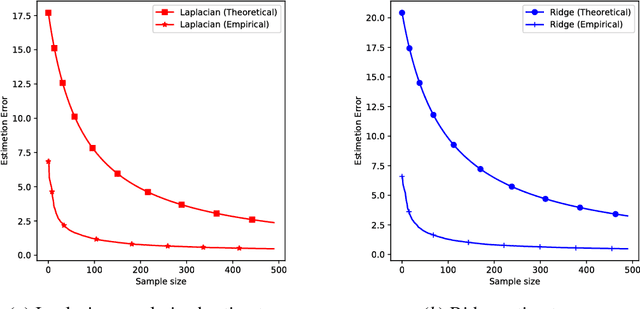
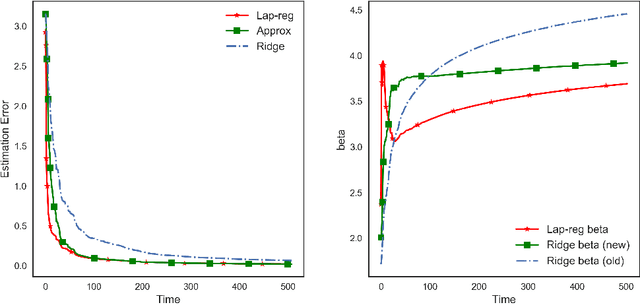
We provide a theoretical analysis of the representation learning problem aimed at learning the latent variables (design matrix) $\Theta$ of observations $Y$ with the knowledge of the coefficient matrix $X$. The design matrix is learned under the assumption that the latent variables $\Theta$ are smooth with respect to a (known) topological structure $\mathcal{G}$. To learn such latent variables, we study a graph Laplacian regularized estimator, which is the penalized least squares estimator with penalty term proportional to a Laplacian quadratic form. This type of estimators has recently received considerable attention due to its capability in incorporating underlying topological graph structure of variables into the learning process. While the estimation problem can be solved efficiently by state-of-the-art optimization techniques, its statistical consistency properties have been largely overlooked. In this work, we develop a non-asymptotic bound of estimation error under the classical statistical setting, where sample size is larger than the ambient dimension of the latent variables. This bound illustrates theoretically the impact of the alignment between the data and the graph structure as well as the graph spectrum on the estimation accuracy. It also provides theoretical evidence of the advantage, in terms of convergence rate, of the graph Laplacian regularized estimator over classical ones (that ignore the graph structure) in case of a smoothness prior. Finally, we provide empirical results of the estimation error to corroborate the theoretical analysis.

Data Driven Chiller Plant Energy Optimization with Domain Knowledge

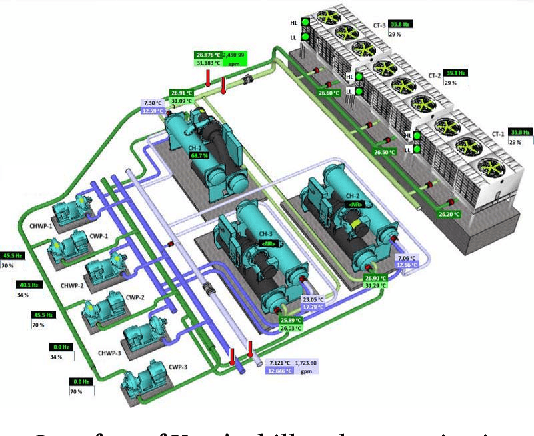
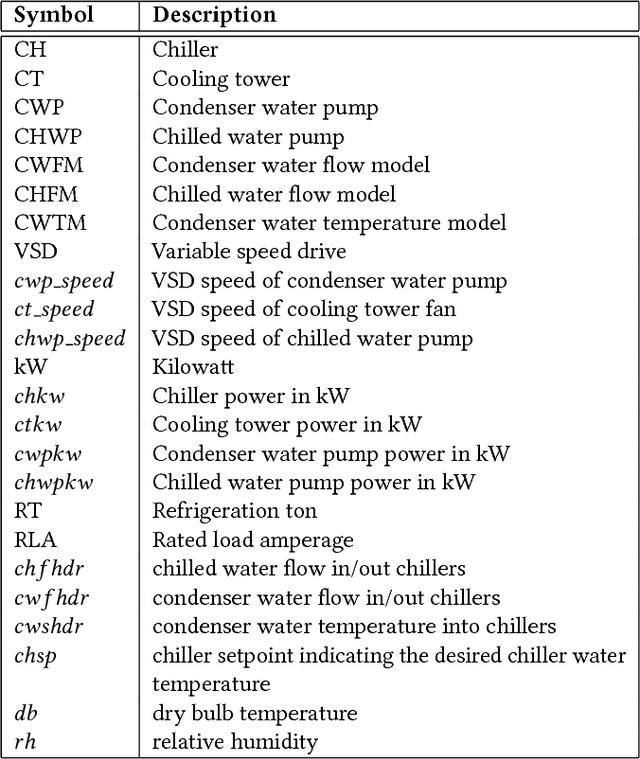
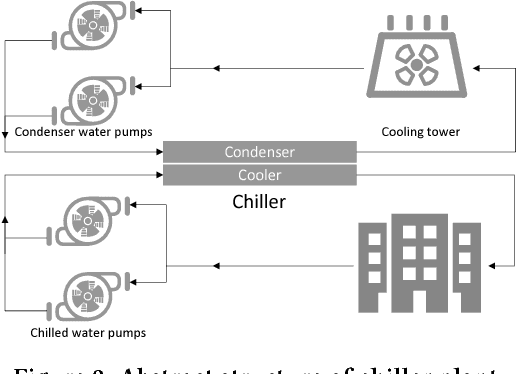
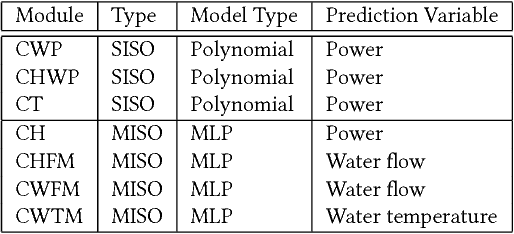
Refrigeration and chiller optimization is an important and well studied topic in mechanical engineering, mostly taking advantage of physical models, designed on top of over-simplified assumptions, over the equipments. Conventional optimization techniques using physical models make decisions of online parameter tuning, based on very limited information of hardware specifications and external conditions, e.g., outdoor weather. In recent years, new generation of sensors is becoming essential part of new chiller plants, for the first time allowing the system administrators to continuously monitor the running status of all equipments in a timely and accurate way. The explosive growth of data flowing to databases, driven by the increasing analytical power by machine learning and data mining, unveils new possibilities of data-driven approaches for real-time chiller plant optimization. This paper presents our research and industrial experience on the adoption of data models and optimizations on chiller plant and discusses the lessons learnt from our practice on real world plants. Instead of employing complex machine learning models, we emphasize the incorporation of appropriate domain knowledge into data analysis tools, which turns out to be the key performance improver over state-of-the-art deep learning techniques by a significant margin. Our empirical evaluation on a real world chiller plant achieves savings by more than 7% on daily power consumption.

Graph-Based Recommendation System

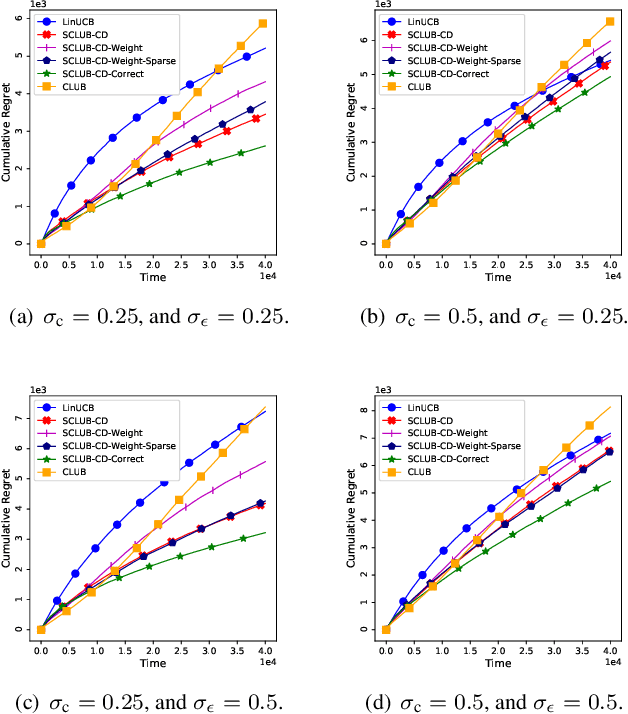
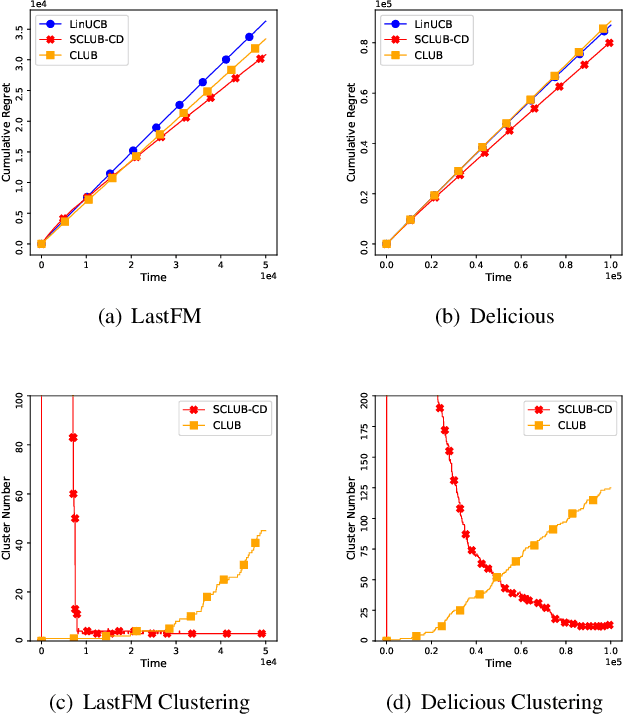
In this work, we study recommendation systems modelled as contextual multi-armed bandit (MAB) problems. We propose a graph-based recommendation system that learns and exploits the geometry of the user space to create meaningful clusters in the user domain. This reduces the dimensionality of the recommendation problem while preserving the accuracy of MAB. We then study the effect of graph sparsity and clusters size on the MAB performance and provide exhaustive simulation results both in synthetic and in real-case datasets. Simulation results show improvements with respect to state-of-the-art MAB algorithms.