Differentiable Linear Bandit Algorithm
Paper and Code
Jun 04, 2020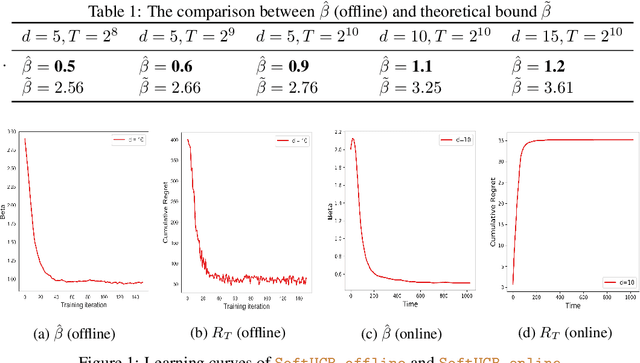
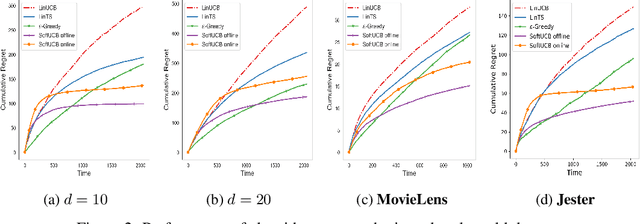
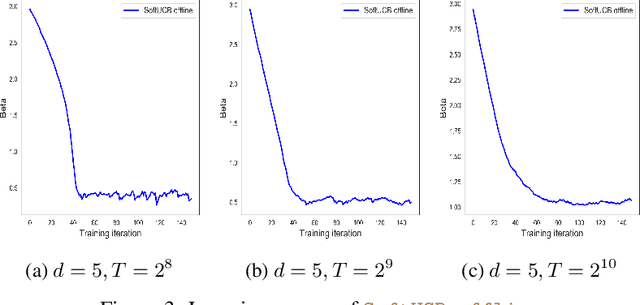
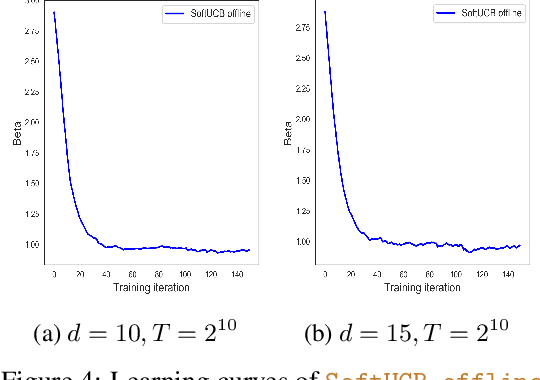
Upper Confidence Bound (UCB) is arguably the most commonly used method for linear multi-arm bandit problems. While conceptually and computationally simple, this method highly relies on the confidence bounds, failing to strike the optimal exploration-exploitation if these bounds are not properly set. In the literature, confidence bounds are typically derived from concentration inequalities based on assumptions on the reward distribution, e.g., sub-Gaussianity. The validity of these assumptions however is unknown in practice. In this work, we aim at learning the confidence bound in a data-driven fashion, making it adaptive to the actual problem structure. Specifically, noting that existing UCB-typed algorithms are not differentiable with respect to confidence bound, we first propose a novel differentiable linear bandit algorithm. Then, we introduce a gradient estimator, which allows the confidence bound to be learned via gradient ascent. Theoretically, we show that the proposed algorithm achieves a $\tilde{\mathcal{O}}(\hat{\beta}\sqrt{dT})$ upper bound of $T$-round regret, where $d$ is the dimension of arm features and $\hat{\beta}$ is the learned size of confidence bound. Empirical results show that $\hat{\beta}$ is significantly smaller than its theoretical upper bound and proposed algorithms outperforms baseline ones on both simulated and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge