Error Analysis on Graph Laplacian Regularized Estimator
Paper and Code
Feb 11, 2019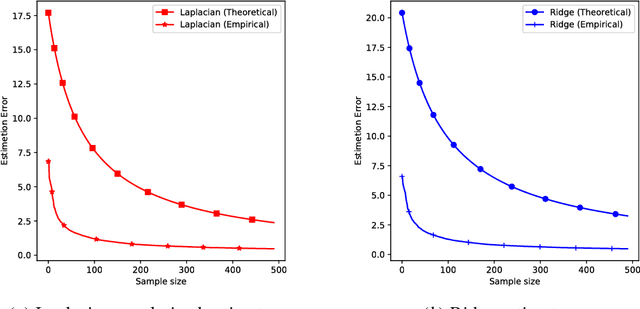
We provide a theoretical analysis of the representation learning problem aimed at learning the latent variables (design matrix) $\Theta$ of observations $Y$ with the knowledge of the coefficient matrix $X$. The design matrix is learned under the assumption that the latent variables $\Theta$ are smooth with respect to a (known) topological structure $\mathcal{G}$. To learn such latent variables, we study a graph Laplacian regularized estimator, which is the penalized least squares estimator with penalty term proportional to a Laplacian quadratic form. This type of estimators has recently received considerable attention due to its capability in incorporating underlying topological graph structure of variables into the learning process. While the estimation problem can be solved efficiently by state-of-the-art optimization techniques, its statistical consistency properties have been largely overlooked. In this work, we develop a non-asymptotic bound of estimation error under the classical statistical setting, where sample size is larger than the ambient dimension of the latent variables. This bound illustrates theoretically the impact of the alignment between the data and the graph structure as well as the graph spectrum on the estimation accuracy. It also provides theoretical evidence of the advantage, in terms of convergence rate, of the graph Laplacian regularized estimator over classical ones (that ignore the graph structure) in case of a smoothness prior. Finally, we provide empirical results of the estimation error to corroborate the theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge