Laplacian-regularized graph bandits: Algorithms and theoretical analysis

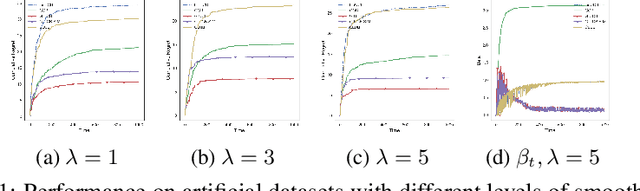
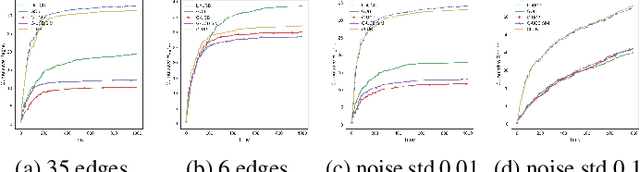
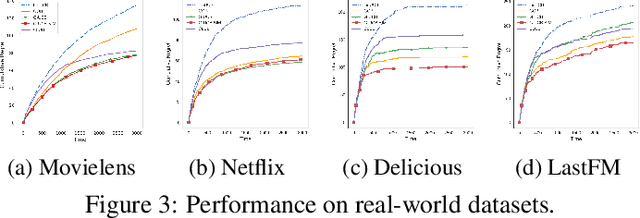
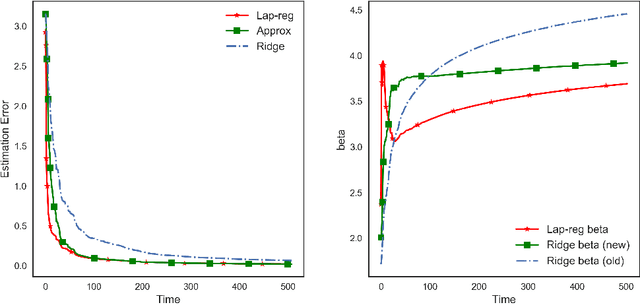
We study contextual multi-armed bandit problems in the case of multiple users, where we exploit the structure in the user domain to reduce the cumulative regret. Specifically, we model user relation as a graph, and assume that the parameters (preferences) of users form smooth signals on the graph. This leads to a graph Laplacian-regularized estimator, for which we propose a novel bandit algorithm whose performance depends on a notion of local smoothness on the graph. We provide a closed-form solution to the estimator, enabling a theoretical analysis on the convergence property of the estimator as well as single-user upper confidence bound (UCB) and cumulative regret of the proposed bandit algorithm. Furthermore, we show that the regret scales linearly with the local smoothness measure, which approaches zero for densely connected graph. The single-user UCB also allows us to further propose an extension of the bandit algorithm, whose computational complexity scales linearly with the number of users. We support theoretical claims with empirical evidences, and demonstrate the advantage of the proposed algorithm in comparison with state-of-the-art graph-based bandit algorithms on both synthetic and real-world datasets.