Multilevel Semantic-Aware Model for AI-Generated Video Quality Assessment

The rapid development of diffusion models has greatly advanced AI-generated videos in terms of length and consistency recently, yet assessing AI-generated videos still remains challenging. Previous approaches have often focused on User-Generated Content(UGC), but few have targeted AI-Generated Video Quality Assessment methods. In this work, we introduce MSA-VQA, a Multilevel Semantic-Aware Model for AI-Generated Video Quality Assessment, which leverages CLIP-based semantic supervision and cross-attention mechanisms. Our hierarchical framework analyzes video content at three levels: frame, segment, and video. We propose a Prompt Semantic Supervision Module using text encoder of CLIP to ensure semantic consistency between videos and conditional prompts. Additionally, we propose the Semantic Mutation-aware Module to capture subtle variations between frames. Extensive experiments demonstrate our method achieves state-of-the-art results.

TAME: Temporal Audio-based Mamba for Enhanced Drone Trajectory Estimation and Classification

The increasing prevalence of compact UAVs has introduced significant risks to public safety, while traditional drone detection systems are often bulky and costly. To address these challenges, we present TAME, the Temporal Audio-based Mamba for Enhanced Drone Trajectory Estimation and Classification. This innovative anti-UAV detection model leverages a parallel selective state-space model to simultaneously capture and learn both the temporal and spectral features of audio, effectively analyzing propagation of sound. To further enhance temporal features, we introduce a Temporal Feature Enhancement Module, which integrates spectral features into temporal data using residual cross-attention. This enhanced temporal information is then employed for precise 3D trajectory estimation and classification. Our model sets a new standard of performance on the MMUAD benchmarks, demonstrating superior accuracy and effectiveness. The code and trained models are publicly available on GitHub \url{https://github.com/AmazingDay1/TAME}.

EDGE: Unknown-aware Multi-label Learning by Energy Distribution Gap Expansion

Multi-label Out-Of-Distribution (OOD) detection aims to discriminate the OOD samples from the multi-label In-Distribution (ID) ones. Compared with its multiclass counterpart, it is crucial to model the joint information among classes. To this end, JointEnergy, which is a representative multi-label OOD inference criterion, summarizes the logits of all the classes. However, we find that JointEnergy can produce an imbalance problem in OOD detection, especially when the model lacks enough discrimination ability. Specifically, we find that the samples only related to minority classes tend to be classified as OOD samples due to the ambiguous energy decision boundary. Besides, imbalanced multi-label learning methods, originally designed for ID ones, would not be suitable for OOD detection scenarios, even producing a serious negative transfer effect. In this paper, we resort to auxiliary outlier exposure (OE) and propose an unknown-aware multi-label learning framework to reshape the uncertainty energy space layout. In this framework, the energy score is separately optimized for tail ID samples and unknown samples, and the energy distribution gap between them is expanded, such that the tail ID samples can have a significantly larger energy score than the OOD ones. What's more, a simple yet effective measure is designed to select more informative OE datasets. Finally, comprehensive experimental results on multiple multi-label and OOD datasets reveal the effectiveness of the proposed method.

HGOE: Hybrid External and Internal Graph Outlier Exposure for Graph Out-of-Distribution Detection

With the progressive advancements in deep graph learning, out-of-distribution (OOD) detection for graph data has emerged as a critical challenge. While the efficacy of auxiliary datasets in enhancing OOD detection has been extensively studied for image and text data, such approaches have not yet been explored for graph data. Unlike Euclidean data, graph data exhibits greater diversity but lower robustness to perturbations, complicating the integration of outliers. To tackle these challenges, we propose the introduction of \textbf{H}ybrid External and Internal \textbf{G}raph \textbf{O}utlier \textbf{E}xposure (HGOE) to improve graph OOD detection performance. Our framework involves using realistic external graph data from various domains and synthesizing internal outliers within ID subgroups to address the poor robustness and presence of OOD samples within the ID class. Furthermore, we develop a boundary-aware OE loss that adaptively assigns weights to outliers, maximizing the use of high-quality OOD samples while minimizing the impact of low-quality ones. Our proposed HGOE framework is model-agnostic and designed to enhance the effectiveness of existing graph OOD detection models. Experimental results demonstrate that our HGOE framework can significantly improve the performance of existing OOD detection models across all 8 real datasets.

ADA-GAD: Anomaly-Denoised Autoencoders for Graph Anomaly Detection

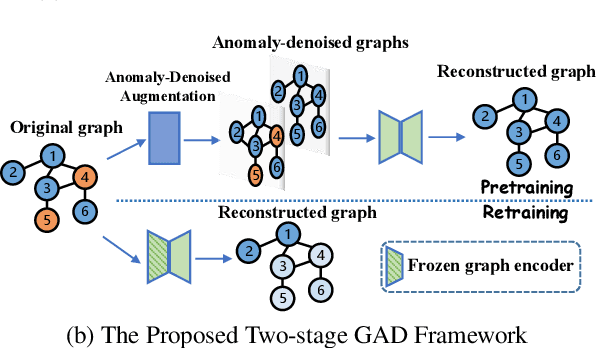
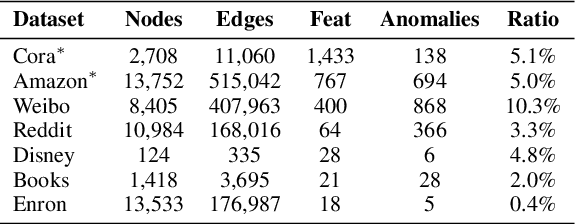
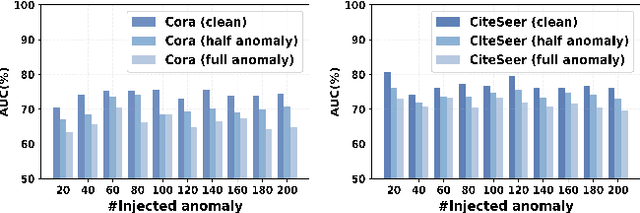
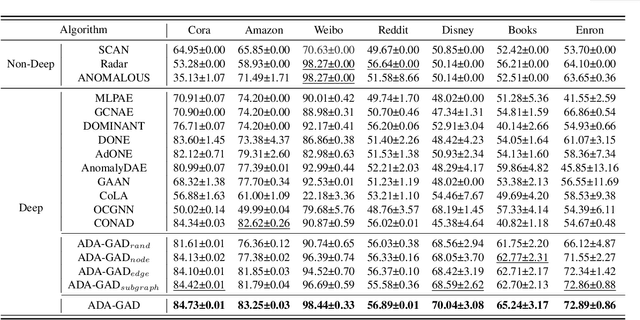
Graph anomaly detection is crucial for identifying nodes that deviate from regular behavior within graphs, benefiting various domains such as fraud detection and social network. Although existing reconstruction-based methods have achieved considerable success, they may face the \textit{Anomaly Overfitting} and \textit{Homophily Trap} problems caused by the abnormal patterns in the graph, breaking the assumption that normal nodes are often better reconstructed than abnormal ones. Our observations indicate that models trained on graphs with fewer anomalies exhibit higher detection performance. Based on this insight, we introduce a novel two-stage framework called Anomaly-Denoised Autoencoders for Graph Anomaly Detection (ADA-GAD). In the first stage, we design a learning-free anomaly-denoised augmentation method to generate graphs with reduced anomaly levels. We pretrain graph autoencoders on these augmented graphs at multiple levels, which enables the graph autoencoders to capture normal patterns. In the next stage, the decoders are retrained for detection on the original graph, benefiting from the multi-level representations learned in the previous stage. Meanwhile, we propose the node anomaly distribution regularization to further alleviate \textit{Anomaly Overfitting}. We validate the effectiveness of our approach through extensive experiments on both synthetic and real-world datasets.

Symbol Detection for Coarsely Quantized OTFS

This paper explicitly models a coarse and noisy quantization in a communication system empowered by orthogonal time frequency space (OTFS) for cost and power efficiency. We first point out, with coarse quantization, the effective channel is imbalanced and thus no longer able to circularly shift the transmitted symbols along the delay-Doppler domain. Meanwhile, the effective channel is non-isotropic, which imposes a significant loss to symbol detection algorithms like the original approximate message passing (AMP). Although the algorithm of generalized expectation consistent for signal recovery (GEC-SR) can mitigate this loss, the complexity in computation is prohibitively high, mainly due to an dramatic increase in the matrix size of OTFS. In this context, we propose a low-complexity algorithm that incorporates into the GEC-SR a quick inversion of quasi-banded matrices, reducing the complexity from a cubic order to a linear order while keeping the performance at the same level.