TempoGPT: Enhancing Temporal Reasoning via Quantizing Embedding

Multi-modal language model has made advanced progress in vision and audio, but still faces significant challenges in dealing with complex reasoning tasks in the time series domain. The reasons are twofold. First, labels for multi-modal time series data are coarse and devoid of analysis or reasoning processes. Training with these data cannot improve the model's reasoning capabilities. Second, due to the lack of precise tokenization in processing time series, the representation patterns for temporal and textual information are inconsistent, which hampers the effectiveness of multi-modal alignment. To address these challenges, we propose a multi-modal time series data construction approach and a multi-modal time series language model (TLM), TempoGPT. Specially, we construct multi-modal data for complex reasoning tasks by analyzing the variable-system relationships within a white-box system. Additionally, proposed TempoGPT achieves consistent representation between temporal and textual information by quantizing temporal embeddings, where temporal embeddings are quantized into a series of discrete tokens using a predefined codebook; subsequently, a shared embedding layer processes both temporal and textual tokens. Extensive experiments demonstrate that TempoGPT accurately perceives temporal information, logically infers conclusions, and achieves state-of-the-art in the constructed complex time series reasoning tasks. Moreover, we quantitatively demonstrate the effectiveness of quantizing temporal embeddings in enhancing multi-modal alignment and the reasoning capabilities of TLMs. Code and data are available at https://github.com/zhanghaochuan20/TempoGPT.

Sensorformer: Cross-patch attention with global-patch compression is effective for high-dimensional multivariate time series forecasting

Among the existing Transformer-based multivariate time series forecasting methods, iTransformer, which treats each variable sequence as a token and only explicitly extracts cross-variable dependencies, and PatchTST, which adopts a channel-independent strategy and only explicitly extracts cross-time dependencies, both significantly outperform most Channel-Dependent Transformer that simultaneously extract cross-time and cross-variable dependencies. This indicates that existing Transformer-based multivariate time series forecasting methods still struggle to effectively fuse these two types of information. We attribute this issue to the dynamic time lags in the causal relationships between different variables. Therefore, we propose a new multivariate time series forecasting Transformer, Sensorformer, which first compresses the global patch information and then simultaneously extracts cross-variable and cross-time dependencies from the compressed representations. Sensorformer can effectively capture the correct inter-variable correlations and causal relationships, even in the presence of dynamic causal lags between variables, while also reducing the computational complexity of pure cross-patch self-attention from $O(D^2 \cdot Patch\_num^2 \cdot d\_model)$ to $O(D^2 \cdot Patch\_num \cdot d\_model)$. Extensive comparative and ablation experiments on 9 mainstream real-world multivariate time series forecasting datasets demonstrate the superiority of Sensorformer. The implementation of Sensorformer, following the style of the Time-series-library and scripts for reproducing the main results, is publicly available at https://github.com/BigYellowTiger/Sensorformer

Symbol Detection for Coarsely Quantized OTFS

This paper explicitly models a coarse and noisy quantization in a communication system empowered by orthogonal time frequency space (OTFS) for cost and power efficiency. We first point out, with coarse quantization, the effective channel is imbalanced and thus no longer able to circularly shift the transmitted symbols along the delay-Doppler domain. Meanwhile, the effective channel is non-isotropic, which imposes a significant loss to symbol detection algorithms like the original approximate message passing (AMP). Although the algorithm of generalized expectation consistent for signal recovery (GEC-SR) can mitigate this loss, the complexity in computation is prohibitively high, mainly due to an dramatic increase in the matrix size of OTFS. In this context, we propose a low-complexity algorithm that incorporates into the GEC-SR a quick inversion of quasi-banded matrices, reducing the complexity from a cubic order to a linear order while keeping the performance at the same level.

Expectation-Maximization-Aided Hybrid Generalized Expectation Consistent for Sparse Signal Reconstruction

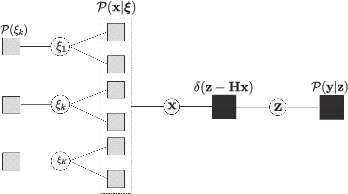
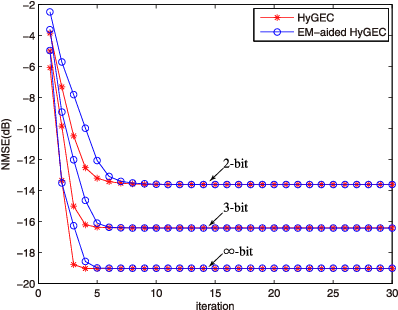
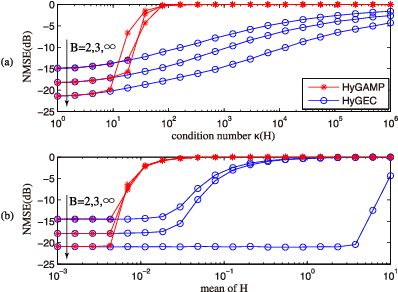
The reconstruction of sparse signal is an active area of research. Different from a typical i.i.d. assumption, this paper considers a non-independent prior of group structure. For this more practical setup, we propose EM-aided HyGEC, a new algorithm to address the stability issue and the hyper-parameter issue facing the other algorithms. The instability problem results from the ill condition of the transform matrix, while the unavailability of the hyper-parameters is a ground truth that their values are not known beforehand. The proposed algorithm is built on the paradigm of HyGAMP (proposed by Rangan et al.) but we replace its inner engine, the GAMP, by a matrix-insensitive alternative, the GEC, so that the first issue is solved. For the second issue, we take expectation-maximization as an outer loop, and together with the inner engine HyGEC, we learn the value of the hyper-parameters. Effectiveness of the proposed algorithm is also verified by means of numerical simulations.