Junchen Ye
Global-Lens Transformers: Adaptive Token Mixing for Dynamic Link Prediction
Nov 16, 2025Abstract:Dynamic graph learning plays a pivotal role in modeling evolving relationships over time, especially for temporal link prediction tasks in domains such as traffic systems, social networks, and recommendation platforms. While Transformer-based models have demonstrated strong performance by capturing long-range temporal dependencies, their reliance on self-attention results in quadratic complexity with respect to sequence length, limiting scalability on high-frequency or large-scale graphs. In this work, we revisit the necessity of self-attention in dynamic graph modeling. Inspired by recent findings that attribute the success of Transformers more to their architectural design than attention itself, we propose GLFormer, a novel attention-free Transformer-style framework for dynamic graphs. GLFormer introduces an adaptive token mixer that performs context-aware local aggregation based on interaction order and time intervals. To capture long-term dependencies, we further design a hierarchical aggregation module that expands the temporal receptive field by stacking local token mixers across layers. Experiments on six widely-used dynamic graph benchmarks show that GLFormer achieves SOTA performance, which reveals that attention-free architectures can match or surpass Transformer baselines in dynamic graph settings with significantly improved efficiency.
DyGKT: Dynamic Graph Learning for Knowledge Tracing
Jul 30, 2024



Abstract:Knowledge Tracing aims to assess student learning states by predicting their performance in answering questions. Different from the existing research which utilizes fixed-length learning sequence to obtain the student states and regards KT as a static problem, this work is motivated by three dynamical characteristics: 1) The scales of students answering records are constantly growing; 2) The semantics of time intervals between the records vary; 3) The relationships between students, questions and concepts are evolving. The three dynamical characteristics above contain the great potential to revolutionize the existing knowledge tracing methods. Along this line, we propose a Dynamic Graph-based Knowledge Tracing model, namely DyGKT. In particular, a continuous-time dynamic question-answering graph for knowledge tracing is constructed to deal with the infinitely growing answering behaviors, and it is worth mentioning that it is the first time dynamic graph learning technology is used in this field. Then, a dual time encoder is proposed to capture long-term and short-term semantics among the different time intervals. Finally, a multiset indicator is utilized to model the evolving relationships between students, questions, and concepts via the graph structural feature. Numerous experiments are conducted on five real-world datasets, and the results demonstrate the superiority of our model. All the used resources are publicly available at https://github.com/PengLinzhi/DyGKT.
Co-Neighbor Encoding Schema: A Light-cost Structure Encoding Method for Dynamic Link Prediction
Jul 30, 2024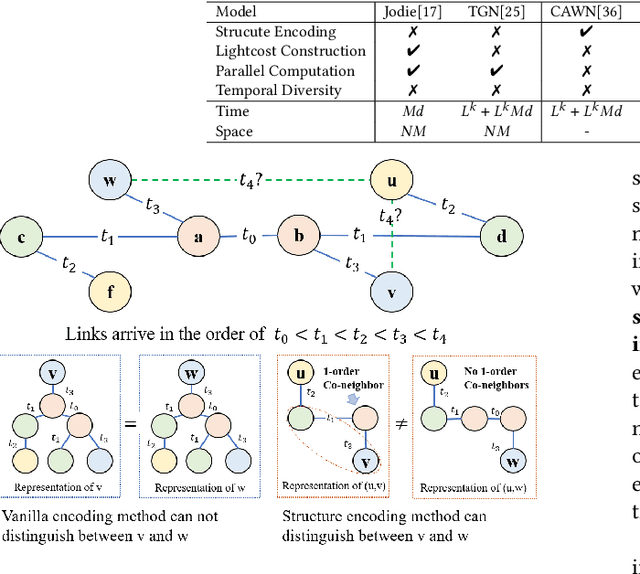

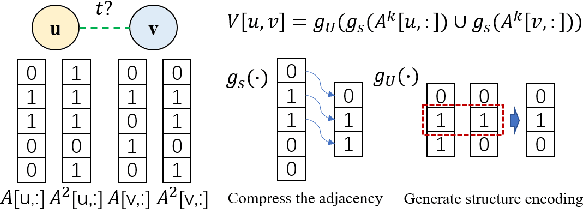
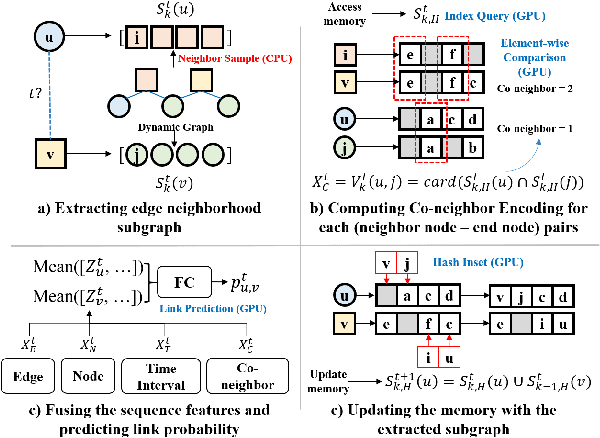
Abstract:Structure encoding has proven to be the key feature to distinguishing links in a graph. However, Structure encoding in the temporal graph keeps changing as the graph evolves, repeatedly computing such features can be time-consuming due to the high-order subgraph construction. We develop the Co-Neighbor Encoding Schema (CNES) to address this issue. Instead of recomputing the feature by the link, CNES stores information in the memory to avoid redundant calculations. Besides, unlike the existing memory-based dynamic graph learning method that stores node hidden states, we introduce a hashtable-based memory to compress the adjacency matrix for efficient structure feature construction and updating with vector computation in parallel. Furthermore, CNES introduces a Temporal-Diverse Memory to generate long-term and short-term structure encoding for neighbors with different structural information. A dynamic graph learning framework, Co-Neighbor Encoding Network (CNE-N), is proposed using the aforementioned techniques. Extensive experiments on thirteen public datasets verify the effectiveness and efficiency of the proposed method.
Repeat-Aware Neighbor Sampling for Dynamic Graph Learning
May 24, 2024Abstract:Dynamic graph learning equips the edges with time attributes and allows multiple links between two nodes, which is a crucial technology for understanding evolving data scenarios like traffic prediction and recommendation systems. Existing works obtain the evolving patterns mainly depending on the most recent neighbor sequences. However, we argue that whether two nodes will have interaction with each other in the future is highly correlated with the same interaction that happened in the past. Only considering the recent neighbors overlooks the phenomenon of repeat behavior and fails to accurately capture the temporal evolution of interactions. To fill this gap, this paper presents RepeatMixer, which considers evolving patterns of first and high-order repeat behavior in the neighbor sampling strategy and temporal information learning. Firstly, we define the first-order repeat-aware nodes of the source node as the destination nodes that have interacted historically and extend this concept to high orders as nodes in the destination node's high-order neighbors. Then, we extract neighbors of the source node that interacted before the appearance of repeat-aware nodes with a slide window strategy as its neighbor sequence. Next, we leverage both the first and high-order neighbor sequences of source and destination nodes to learn temporal patterns of interactions via an MLP-based encoder. Furthermore, considering the varying temporal patterns on different orders, we introduce a time-aware aggregation mechanism that adaptively aggregates the temporal representations from different orders based on the significance of their interaction time sequences. Experimental results demonstrate the superiority of RepeatMixer over state-of-the-art models in link prediction tasks, underscoring the effectiveness of the proposed repeat-aware neighbor sampling strategy.
Learning the Evolutionary and Multi-scale Graph Structure for Multivariate Time Series Forecasting
Jun 28, 2022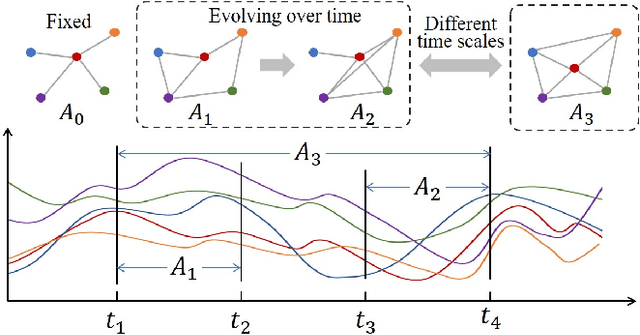
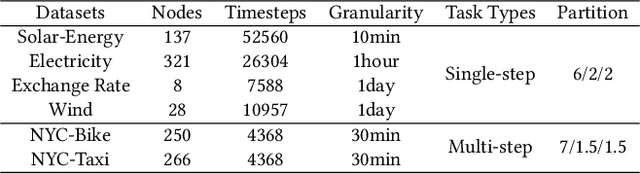
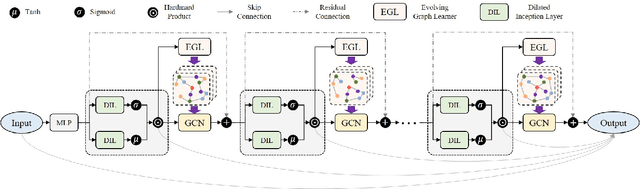
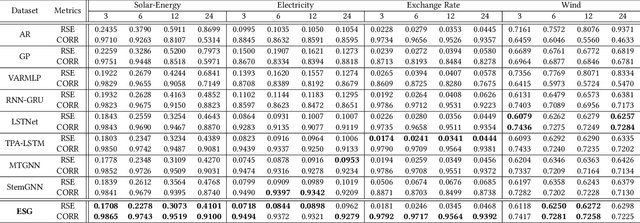
Abstract:Recent studies have shown great promise in applying graph neural networks for multivariate time series forecasting, where the interactions of time series are described as a graph structure and the variables are represented as the graph nodes. Along this line, existing methods usually assume that the graph structure (or the adjacency matrix), which determines the aggregation manner of graph neural network, is fixed either by definition or self-learning. However, the interactions of variables can be dynamic and evolutionary in real-world scenarios. Furthermore, the interactions of time series are quite different if they are observed at different time scales. To equip the graph neural network with a flexible and practical graph structure, in this paper, we investigate how to model the evolutionary and multi-scale interactions of time series. In particular, we first provide a hierarchical graph structure cooperated with the dilated convolution to capture the scale-specific correlations among time series. Then, a series of adjacency matrices are constructed under a recurrent manner to represent the evolving correlations at each layer. Moreover, a unified neural network is provided to integrate the components above to get the final prediction. In this way, we can capture the pair-wise correlations and temporal dependency simultaneously. Finally, experiments on both single-step and multi-step forecasting tasks demonstrate the superiority of our method over the state-of-the-art approaches.
Analysis for full face mechanical behaviors through spatial deduction model with real-time monitoring data
Sep 27, 2021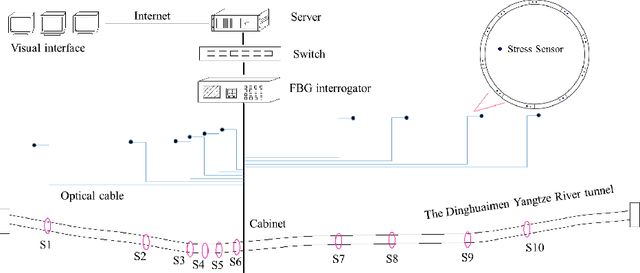
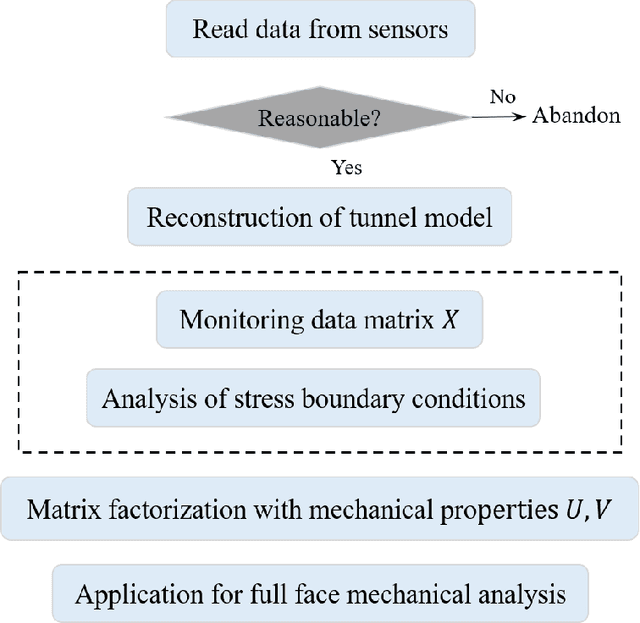
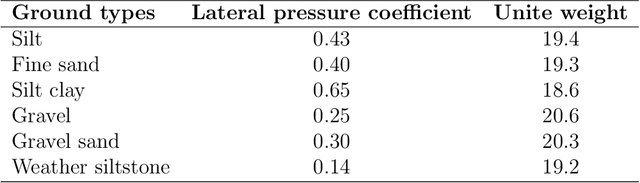
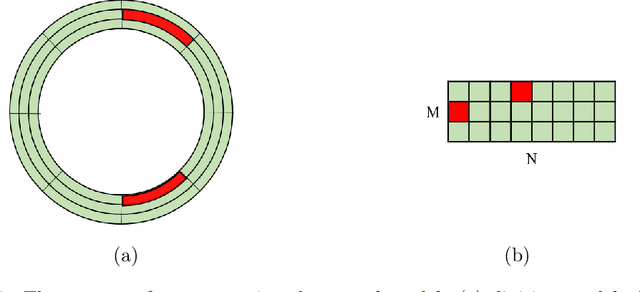
Abstract:Mechanical analysis for the full face of tunnel structure is crucial to maintain stability, which is a challenge in classical analytical solutions and data analysis. Along this line, this study aims to develop a spatial deduction model to obtain the full-faced mechanical behaviors through integrating mechanical properties into pure data-driven model. The spatial tunnel structure is divided into many parts and reconstructed in a form of matrix. Then, the external load applied on structure in the field was considered to study the mechanical behaviors of tunnel. Based on the limited observed monitoring data in matrix and mechanical analysis results, a double-driven model was developed to obtain the full-faced information, in which the data-driven model was the dominant one and the mechanical constraint was the secondary one. To verify the presented spatial deduction model, cross-test was conducted through assuming partial monitoring data are unknown and regarding them as testing points. The well agreement between deduction results with actual monitoring results means the proposed model is reasonable. Therefore, it was employed to deduct both the current and historical performance of tunnel full face, which is crucial to prevent structural disasters.
Coupled Layer-wise Graph Convolution for Transportation Demand Prediction
Dec 15, 2020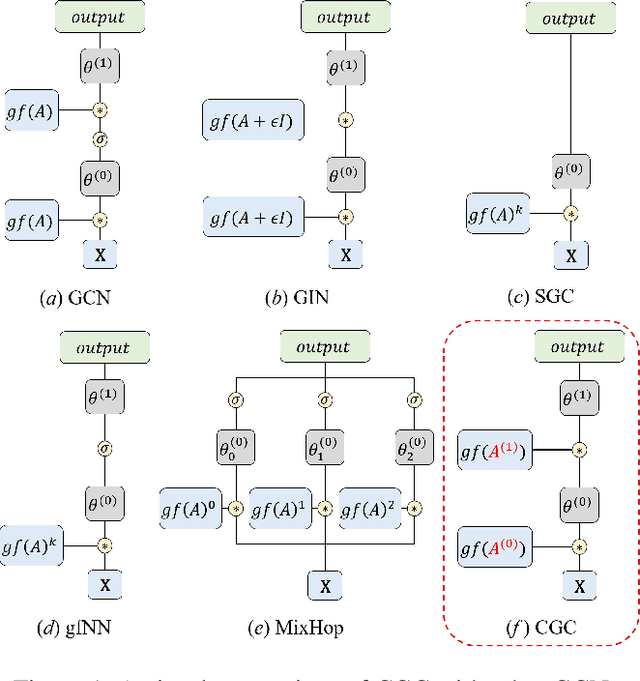
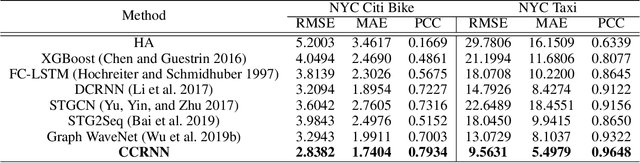
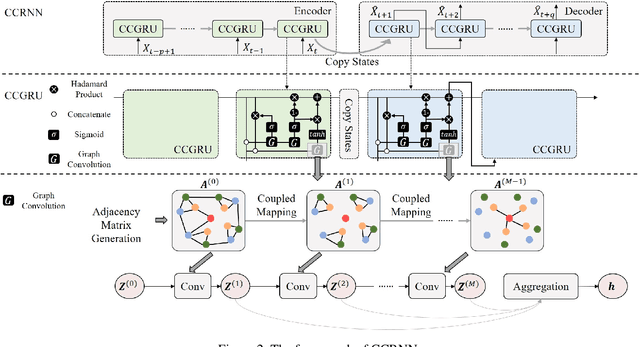
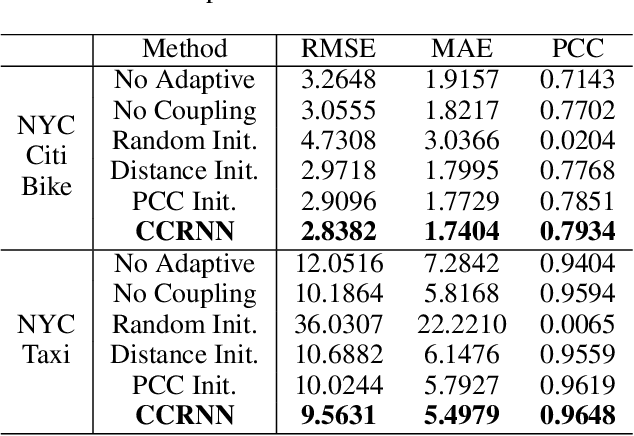
Abstract:Graph Convolutional Network (GCN) has been widely applied in transportation demand prediction due to its excellent ability to capture non-Euclidean spatial dependence among station-level or regional transportation demands. However, in most of the existing research, the graph convolution was implemented on a heuristically generated adjacency matrix, which could neither reflect the real spatial relationships of stations accurately, nor capture the multi-level spatial dependence of demands adaptively. To cope with the above problems, this paper provides a novel graph convolutional network for transportation demand prediction. Firstly, a novel graph convolution architecture is proposed, which has different adjacency matrices in different layers and all the adjacency matrices are self-learned during the training process. Secondly, a layer-wise coupling mechanism is provided, which associates the upper-level adjacency matrix with the lower-level one. It also reduces the scale of parameters in our model. Lastly, a unitary network is constructed to give the final prediction result by integrating the hidden spatial states with gated recurrent unit, which could capture the multi-level spatial dependence and temporal dynamics simultaneously. Experiments have been conducted on two real-world datasets, NYC Citi Bike and NYC Taxi, and the results demonstrate the superiority of our model over the state-of-the-art ones.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge