Junbum Shin
HETAL: Efficient Privacy-preserving Transfer Learning with Homomorphic Encryption
Mar 21, 2024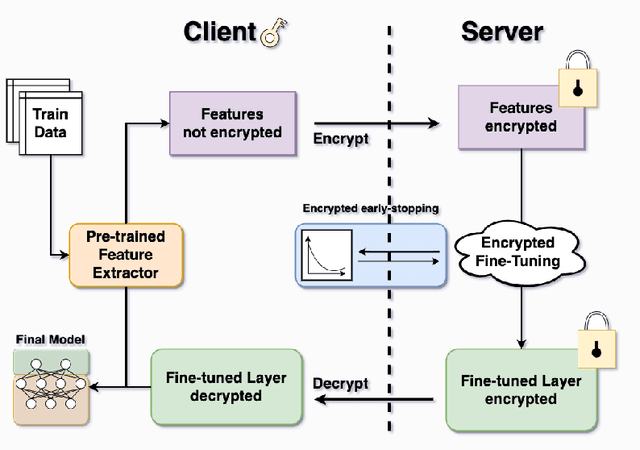
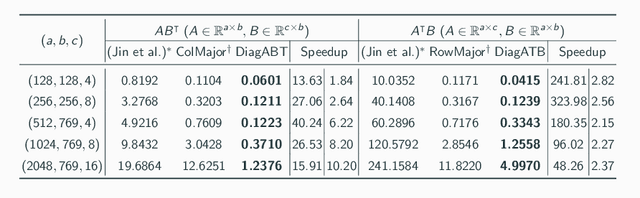
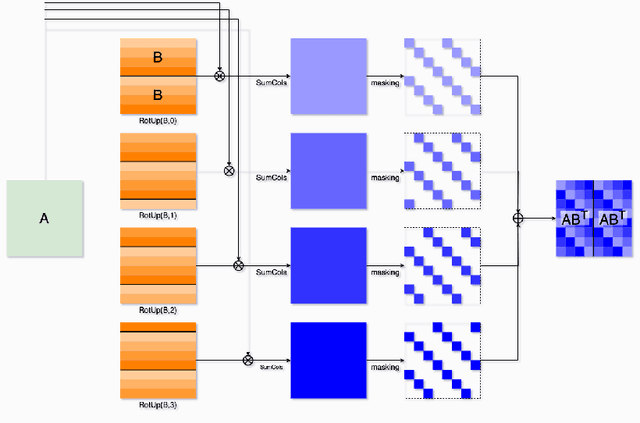
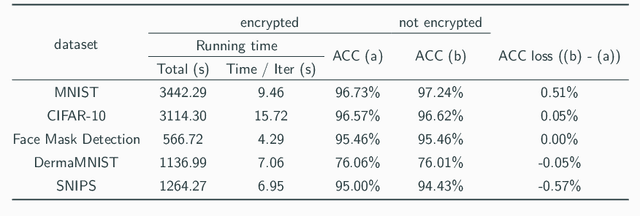
Abstract:Transfer learning is a de facto standard method for efficiently training machine learning models for data-scarce problems by adding and fine-tuning new classification layers to a model pre-trained on large datasets. Although numerous previous studies proposed to use homomorphic encryption to resolve the data privacy issue in transfer learning in the machine learning as a service setting, most of them only focused on encrypted inference. In this study, we present HETAL, an efficient Homomorphic Encryption based Transfer Learning algorithm, that protects the client's privacy in training tasks by encrypting the client data using the CKKS homomorphic encryption scheme. HETAL is the first practical scheme that strictly provides encrypted training, adopting validation-based early stopping and achieving the accuracy of nonencrypted training. We propose an efficient encrypted matrix multiplication algorithm, which is 1.8 to 323 times faster than prior methods, and a highly precise softmax approximation algorithm with increased coverage. The experimental results for five well-known benchmark datasets show total training times of 567-3442 seconds, which is less than an hour.
Collecting and Analyzing Multidimensional Data with Local Differential Privacy
Jun 28, 2019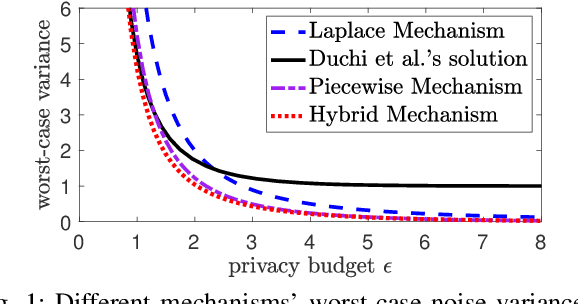
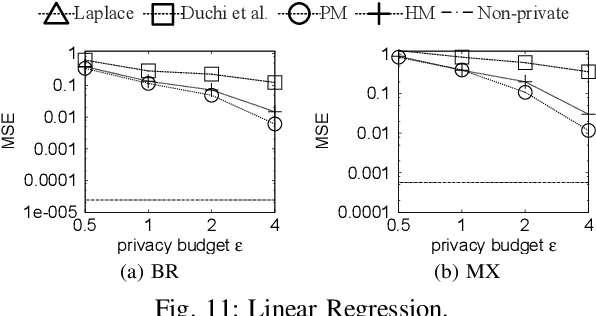
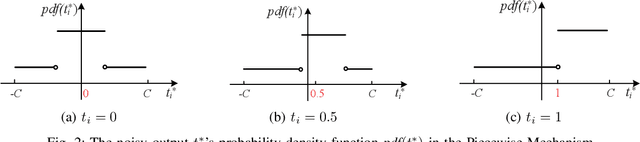
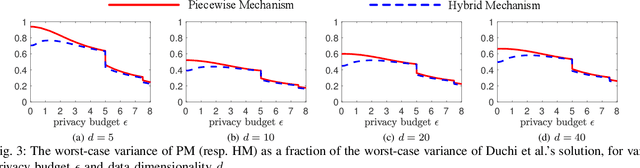
Abstract:Local differential privacy (LDP) is a recently proposed privacy standard for collecting and analyzing data, which has been used, e.g., in the Chrome browser, iOS and macOS. In LDP, each user perturbs her information locally, and only sends the randomized version to an aggregator who performs analyses, which protects both the users and the aggregator against private information leaks. Although LDP has attracted much research attention in recent years, the majority of existing work focuses on applying LDP to complex data and/or analysis tasks. In this paper, we point out that the fundamental problem of collecting multidimensional data under LDP has not been addressed sufficiently, and there remains much room for improvement even for basic tasks such as computing the mean value over a single numeric attribute under LDP. Motivated by this, we first propose novel LDP mechanisms for collecting a numeric attribute, whose accuracy is at least no worse (and usually better) than existing solutions in terms of worst-case noise variance. Then, we extend these mechanisms to multidimensional data that can contain both numeric and categorical attributes, where our mechanisms always outperform existing solutions regarding worst-case noise variance. As a case study, we apply our solutions to build an LDP-compliant stochastic gradient descent algorithm (SGD), which powers many important machine learning tasks. Experiments using real datasets confirm the effectiveness of our methods, and their advantages over existing solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge